using OrdinaryDiffEq
using ComponentArrays
using SimpleUnPack
using Plots
Plots.default(linewidth=2)Fig 7.23
Hasty synthetic oscillator model
_dx723(u, p, t) = (1 + u.x^2 + p.alpha * p.sigma * u.x^4) / ((1 + u.x^2 + p.sigma * u.x^4) * (1 + u.y^4)) - p.gammax * u.x
_dy723(u, p, t) = p.ax * ((1 + u.x^2 + p.alpha * p.sigma * u.x^4) / ((1 + u.x^2 + p.sigma * u.x^4) * (1 + u.y^4))) - p.gammay * u.y
function model723!(D, u, p, t)
@unpack alpha, sigma, gammax, gammay, ax = p
@unpack x, y = u
D.x = _dx723(u, p, t)
D.y = _dy723(u, p, t)
nothing
endmodel723! (generic function with 1 method)ps723 = ComponentArray(
alpha=11.0,
sigma=2.0,
gammax=0.2,
gammay=0.012,
ax=0.2,
)
ics723 = ComponentArray(
x=0.3963,
y=2.3346,
)
tend = 300.0
prob723 = ODEProblem(model723!, ics723, (0.0, tend), ps723)ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(x = 1, y = 2)}}} and tType Float64. In-place: true Non-trivial mass matrix: false timespan: (0.0, 300.0) u0: ComponentVector{Float64}(x = 0.3963, y = 2.3346)
@time sol723 = solve(prob723, Tsit5()) 2.117523 seconds (8.17 M allocations: 410.954 MiB, 2.43% gc time, 99.99% compilation time)retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 46-element Vector{Float64}:
0.0
0.17572779495437757
1.9330057444981532
5.344184839285967
8.441583349879416
12.371755128086045
16.77146728753059
22.694473602418057
28.953453196286056
35.528404417336496
⋮
240.8048452346208
248.26457018938274
256.5649998648016
264.3832134566723
271.30839266914506
278.0060276504212
285.3504040217544
293.35636434600667
300.0
u: 46-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(x = 1, y = 2)}}}}:
ComponentVector{Float64}(x = 0.3963, y = 2.3346)
ComponentVector{Float64}(x = 0.39049835018421125, y = 2.3312852864277915)
ComponentVector{Float64}(x = 0.33962659154985064, y = 2.297886114522172)
ComponentVector{Float64}(x = 0.2762863007069301, y = 2.2339980392417558)
ComponentVector{Float64}(x = 0.25070196969565717, y = 2.1792665253912493)
ComponentVector{Float64}(x = 0.24602050004702355, y = 2.1158056120922275)
ComponentVector{Float64}(x = 0.2622810480341912, y = 2.0535166800213323)
ComponentVector{Float64}(x = 0.30505960512864105, y = 1.9854619869790682)
ComponentVector{Float64}(x = 0.3737128130380298, y = 1.9364409743500586)
ComponentVector{Float64}(x = 0.505000606019007, y = 1.9239871103005297)
⋮
ComponentVector{Float64}(x = 0.2585069178832619, y = 2.062935097678075)
ComponentVector{Float64}(x = 0.312516378860336, y = 1.9775238765769576)
ComponentVector{Float64}(x = 0.41835468999535197, y = 1.924277293507833)
ComponentVector{Float64}(x = 0.7118771925185501, y = 1.967078853327622)
ComponentVector{Float64}(x = 1.381980796941657, y = 2.2244279877489572)
ComponentVector{Float64}(x = 1.3370822019098099, y = 2.4041988259910094)
ComponentVector{Float64}(x = 1.0270886768840066, y = 2.474906086989245)
ComponentVector{Float64}(x = 0.6637336938277042, y = 2.4366624183401475)
ComponentVector{Float64}(x = 0.38546944983025233, y = 2.3280104088377125)
plot(sol723, xlabel="Time", ylabel="Concentration", title="Fig 7.23 A", labels=["x" "y"])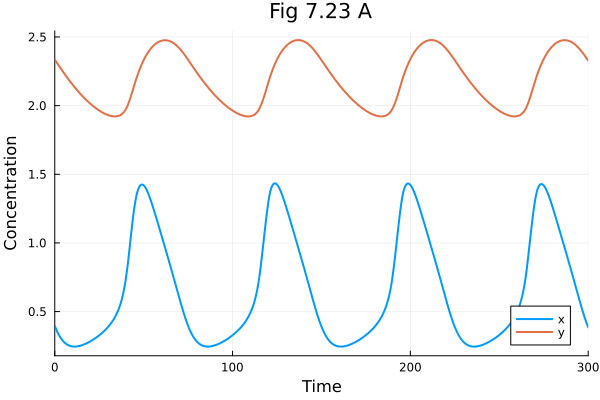
∂X723 = (x, y) -> _dx723(ComponentArray(x=x, y=y), ps723, nothing)
∂Y723 = (x, y) -> _dy723(ComponentArray(x=x, y=y), ps723, nothing)#5 (generic function with 1 method)Grid points
rX = range(0, 1.5, 31)
rY = range(0, 3, 31)
xx = [x for y in rY, x in rX]
yy = [y for y in rY, x in rX];Vector field
fig = plot(title="Fig 7.23 B")
contour!(fig, rX, rY, ∂X723, levels=[0], cbar=false, line=(:black))
plot!(fig, Float64[], Float64[], line=(:black), label="X nullcline")
contour!(fig, rX, rY, ∂Y723, levels=[0], cbar=false, line=(:dot, :black))
plot!(fig, Float64[], Float64[], line=(:dot, :black), label="Y nullcline")
plot!(sol723, idxs=(1,2), lw=2, label=false)
plot!(fig, xlims=(0.0, 1.5), ylims=(1.5, 3.0), xlabel="X", ylabel="Y")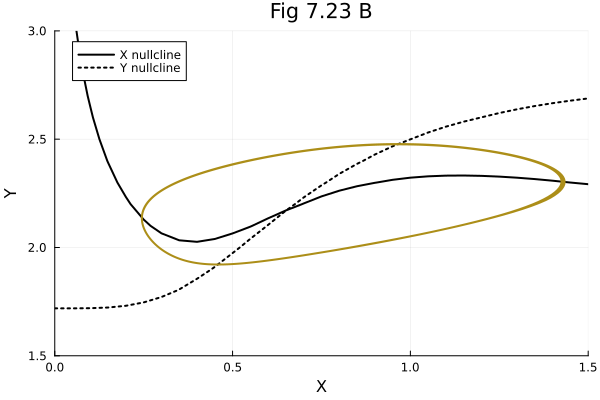
This notebook was generated using Literate.jl.
Back to top