using ComponentArrays
using SimpleUnPack
using DiffEqCallbacks
using OrdinaryDiffEq
using SteadyStateDiffEq
using Plots
Plots.default(linewidth=2)Fig 7.7
model of lac operon in E. coli
hil(x, k) = x / (x + k)
hil(x, k, n) = hil(x^n, k^n)
function model707!(D, u, p, t)
@unpack Le, a1, RToverK1, K2, δM, δY, δL, c1, kL, KML, kg, KMg = p
@unpack M, Y, L = u
D.M = a1 / (1 + RToverK1 * (K2 / (K2 + L))^4) - δM * M
D.Y = c1 * M - δY * Y
D.L = kL * Y * hil(Le, KML) - 2kg * (Y/4) * hil(L, KMg) - δL * L
nothing
endmodel707! (generic function with 1 method)ps707 = ComponentArray(
δM = 0.48,
δY = 0.03,
δL = 0.02,
a1 = 0.29,
K2 = 2.92e6,
RToverK1 = 213.2,
c1 = 18.8,
kL = 6e4,
KML = 680.0,
kg = 3.6e3,
KMg = 7e5,
Le = 0.0,
)
ics707 = ComponentArray(
M = 0.01,
Y = 0.1,
L = 0.0,
)ComponentVector{Float64}(M = 0.01, Y = 0.1, L = 0.0)
Events
affect_le1!(integrator) = integrator.p.Le = 50
affect_le2!(integrator) = integrator.p.Le = 100
affect_le3!(integrator) = integrator.p.Le = 150
affect_le4!(integrator) = integrator.p.Le = 0
event_le1 = PresetTimeCallback([500.0], affect_le1!)
event_le2 = PresetTimeCallback([1000.0], affect_le2!)
event_le3 = PresetTimeCallback([1500.0], affect_le3!)
event_le4 = PresetTimeCallback([2000.0], affect_le4!)
cbs = CallbackSet(event_le1, event_le2, event_le3, event_le4)SciMLBase.CallbackSet{Tuple{}, Tuple{SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le1!)}, typeof(Main.var"##335".affect_le1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le2!)}, typeof(Main.var"##335".affect_le2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le3!)}, typeof(Main.var"##335".affect_le3!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le3!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le4!)}, typeof(Main.var"##335".affect_le4!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le4!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}}}((), (SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le1!)}, typeof(Main.var"##335".affect_le1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le1!)}([500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le1!), Main.var"##335".affect_le1!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le1!)}([500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le1!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le2!)}, typeof(Main.var"##335".affect_le2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le2!)}([1000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le2!), Main.var"##335".affect_le2!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le2!)}([1000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le2!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le3!)}, typeof(Main.var"##335".affect_le3!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le3!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le3!)}([1500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le3!), Main.var"##335".affect_le3!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le3!)}([1500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le3!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le4!)}, typeof(Main.var"##335".affect_le4!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le4!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le4!)}([2000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le4!), Main.var"##335".affect_le4!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##335".affect_le4!)}([2000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##335".affect_le4!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ())))Fig 7.07 (A)
tend = 2500.0
prob707a = ODEProblem(model707!, ics707, tend, ps707)
@time sol = solve(prob707a, Tsit5(), callback=cbs) 3.169256 seconds (9.01 M allocations: 450.991 MiB, 4.14% gc time, 99.99% compilation time)retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 383-element Vector{Float64}:
0.0
0.09860293096459208
0.480090262806086
1.0838771988774543
1.8184532581758965
2.764101968548501
3.881592609434633
5.211149891394837
6.752008012178124
8.549305573366425
⋮
2446.278062522656
2453.5838755111404
2460.88970297681
2468.1955781064858
2475.5014996757654
2482.8074479173893
2490.1134015603093
2497.419348409862
2500.0
u: 383-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(M = 1, Y = 2, L = 3)}}}}:
ComponentVector{Float64}(M = 0.01, Y = 0.1, L = 0.0)
ComponentVector{Float64}(M = 0.009668117807722, Y = 0.11790485819855034, L = 0.0)
ComponentVector{Float64}(M = 0.008522340648285396, Y = 0.1812895622544918, L = 0.0)
ComponentVector{Float64}(M = 0.007087775968801919, Y = 0.2654209332959013, L = 0.0)
ComponentVector{Float64}(M = 0.00581982322060085, Y = 0.3472484248683443, L = 0.0)
ComponentVector{Float64}(M = 0.004725517086593115, Y = 0.42918855968930764, L = 0.0)
ComponentVector{Float64}(M = 0.0039346907681863975, Y = 0.5037284321642758, L = 0.0)
ComponentVector{Float64}(M = 0.0034091165370090265, Y = 0.5732836892562777, L = 0.0)
ComponentVector{Float64}(M = 0.0031015012460018088, Y = 0.6389741606094332, L = 0.0)
ComponentVector{Float64}(M = 0.0029391530114797368, Y = 0.7043812732676594, L = 0.0)
⋮
ComponentVector{Float64}(M = 0.0028223045805549807, Y = 1.7742677735561916, L = 5.3474605308773014e-8)
ComponentVector{Float64}(M = 0.0028223044034524497, Y = 1.7729331058459583, L = 4.469091291308353e-8)
ComponentVector{Float64}(M = 0.0028223042480476006, Y = 1.7718611238835784, L = 3.735084993916307e-8)
ComponentVector{Float64}(M = 0.002822304164028839, Y = 1.7710001212887614, L = 3.121685141972671e-8)
ComponentVector{Float64}(M = 0.0028223041495520724, Y = 1.7703085749480925, L = 2.609056709513414e-8)
ComponentVector{Float64}(M = 0.002822304175014983, Y = 1.7697531360639984, L = 2.1806337165936985e-8)
ComponentVector{Float64}(M = 0.0028223042085664643, Y = 1.7693070187131013, L = 1.822577223546863e-8)
ComponentVector{Float64}(M = 0.0028223042319456466, Y = 1.768948707402647, L = 1.5233247403820682e-8)
ComponentVector{Float64}(M = 0.0028210760041431104, Y = 1.7688910903315862, L = 1.4298130899787112e-8)
plot(sol, idxs=[2], label="β-galactosidase monomer")
plot!(t -> 50 * (500<=t<1000) + 100 * (1000<=t<1500) + 150 * (1500<=t<2000), 0, tend, xlabel="Time (min)", title="Fig 7.7 (A)", label="External lactose")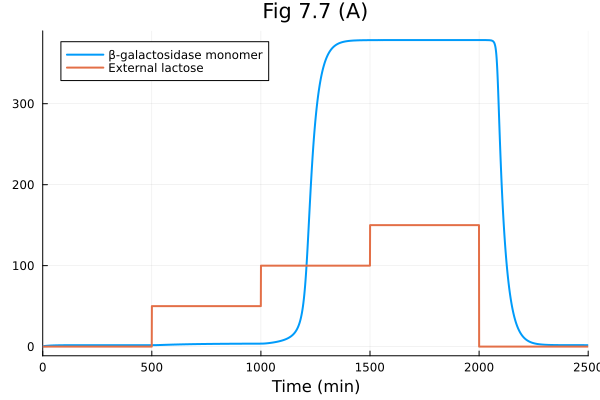
Fig 7.07 (B)
Compare the original model and the modified model
function model707b!(D, u, p, t)
@unpack Le, a1, RToverK1, K2, δM, δY, δL, c1, kL, KML, kg, KMg, Enz = p
@unpack M, Y, L = u
D.M = a1 / (1 + RToverK1 * (K2 / (K2 + L))^4) - δM * M
D.Y = c1 * M - δY * Y
D.L = 4kL * Enz * hil(Le, KML) - 2kg * Enz * hil(L, KMg) - δL * L
nothing
endmodel707b! (generic function with 1 method)ps707b = ComponentArray(ps707; Enz=40.0)
prob707a = SteadyStateProblem(model707!, ics707, ps707)
prob707b = SteadyStateProblem(model707b!, ics707, ps707b)
lerange = range(0, 100, 101)
eprob = EnsembleProblem(prob707a;
prob_func=(prob, i, repeat) -> remake(prob, p=ComponentArray(ps707; Le=lerange[i])),
output_func=(sol, i) -> (sol.u.Y / 4, false)
)
eprob_mod = EnsembleProblem(prob707b;
prob_func=(prob, i, repeat) -> remake(prob, p=ComponentArray(ps707b; Le=lerange[i])),
output_func=(sol, i) -> (sol.u.Y / 4, false)
)
alg = DynamicSS(FBDF())
opts = (trajectories=length(lerange), abstol=1e-9, reltol=1e-9)
@time sim = solve(eprob, alg; opts...)
@time sim_mod = solve(eprob_mod, alg; opts...)
fig = plot(lerange, sim.u, label="Original")
fig = plot!(fig, lerange, sim_mod.u, label="Modified")
fig = plot!(fig,
xlabel="External lactose concentration (μM)",
ylabel="β-galactosidase",
title="Fig 7.7 (B)"
) 7.330054 seconds (35.25 M allocations: 1.556 GiB, 4.07% gc time, 185.13% compilation time)
3.343326 seconds (13.03 M allocations: 634.868 MiB, 2.75% gc time, 183.73% compilation time)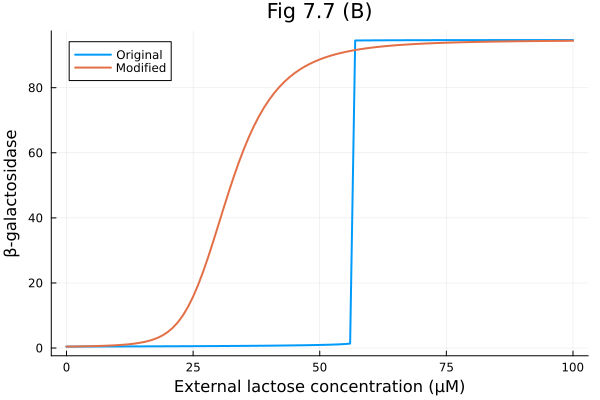
This notebook was generated using Literate.jl.