using OrdinaryDiffEq
using ComponentArrays
using DiffEqCallbacks
using SimpleUnPack
using Plots
Plots.default(linewidth=2)Fig 1.09
Hodgkin-Huxley model
Convenience functions
hil(x, k) = x / (x + k)
hil(x, k, n) = hil(x^n, k^n)
exprel(x) = x / expm1(x)
_mα(u, p, t) = exprel(-0.10 * (u.v + 35))
_mβ(u, p, t) = 4.0 * exp(-(u.v + 60) / 18.0)
_hα(u, p, t) = 0.07 * exp(-(u.v + 60) / 20)
_hβ(u, p, t) = 1 / (exp(-(u.v + 30) / 10) + 1)
_nα(u, p, t) = 0.1 * exprel(-0.1 * (u.v + 50))
_nβ(u, p, t) = 0.125 * exp(-(u.v + 60) / 80)
_iNa(u, p, t) = p.G_N_BAR * (u.v - p.E_N) * (u.m^3) * u.h
_iK(u, p, t) = p.G_K_BAR * (u.v - p.E_K) * (u.n^4)
_iLeak(u, p, t) = p.G_LEAK * (u.v - p.E_LEAK)_iLeak (generic function with 1 method)HH Neuron model
function hh_neuron!(du, u, p, t)
@unpack E_N, E_K, E_LEAK, G_N_BAR, G_K_BAR, G_LEAK, C_M, iStim = p
@unpack v, m, h, n = u
mα = _mα(u, p, t)
mβ = _mβ(u, p, t)
hα = _hα(u, p, t)
hβ = _hβ(u, p, t)
nα = _nα(u, p, t)
nβ = _nβ(u, p, t)
iNa = _iNa(u, p, t)
iK = _iK(u, p, t)
iLeak = _iLeak(u, p, t)
du.v = -(iNa + iK + iLeak + iStim) / C_M
du.m = -(mα + mβ) * m + mα
du.h = -(hα + hβ) * h + hα
du.n = -(nα + nβ) * n + nα
nothing
endhh_neuron! (generic function with 1 method)Problem definition
ps = ComponentArray(
E_N = 55.0, ## Reversal potential of Na (mV)
E_K = -72.0, ## Reversal potential of K (mV)
E_LEAK = -49.0, ## Reversal potential of leaky channels (mV)
G_N_BAR = 120.0, ## Max. Na channel conductance (mS/cm^2)
G_K_BAR = 36.0, ## Max. K channel conductance (mS/cm^2)
G_LEAK = 0.30, ## Max. leak channel conductance (mS/cm^2)
C_M = 1.0, ## membrane capacitance (uF/cm^2))
iStim = 0.0 ## stimulation current
)
u0 = ComponentArray(
v = -59.8977,
m = 0.0536,
h = 0.5925,
n = 0.3192,
)
tspan = (0.0, 100.0)
prob = ODEProblem(hh_neuron!, u0, tspan, ps)ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(v = 1, m = 2, h = 3, n = 4)}}} and tType Float64. In-place: true Non-trivial mass matrix: false timespan: (0.0, 100.0) u0: ComponentVector{Float64}(v = -59.8977, m = 0.0536, h = 0.5925, n = 0.3192)
Callbacks for stimulation current
affect_stim_on1!(integrator) = integrator.p.iStim = -6.6
affect_stim_off1!(integrator) = integrator.p.iStim = 0.0
affect_stim_on2!(integrator) = integrator.p.iStim = -6.9
affect_stim_off2!(integrator) = integrator.p.iStim = 0.0
cb_stim_on1 = PresetTimeCallback(20.0, affect_stim_on1!)
cb_stim_off1 = PresetTimeCallback(21.0, affect_stim_off1!)
cb_stim_on2 = PresetTimeCallback(60.0, affect_stim_on2!)
cb_stim_off2 = PresetTimeCallback(61.0, affect_stim_off2!)
cbs = CallbackSet(cb_stim_on1, cb_stim_off1, cb_stim_on2, cb_stim_off2)SciMLBase.CallbackSet{Tuple{}, Tuple{SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on1!)}, typeof(Main.var"##296".affect_stim_on1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off1!)}, typeof(Main.var"##296".affect_stim_off1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on2!)}, typeof(Main.var"##296".affect_stim_on2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off2!)}, typeof(Main.var"##296".affect_stim_off2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}}}((), (SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on1!)}, typeof(Main.var"##296".affect_stim_on1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on1!)}([20.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_on1!), Main.var"##296".affect_stim_on1!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on1!)}([20.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_on1!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off1!)}, typeof(Main.var"##296".affect_stim_off1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off1!)}([21.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_off1!), Main.var"##296".affect_stim_off1!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off1!)}([21.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_off1!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on2!)}, typeof(Main.var"##296".affect_stim_on2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on2!)}([60.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_on2!), Main.var"##296".affect_stim_on2!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_on2!)}([60.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_on2!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off2!)}, typeof(Main.var"##296".affect_stim_off2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off2!)}([61.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_off2!), Main.var"##296".affect_stim_off2!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##296".affect_stim_off2!)}([61.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##296".affect_stim_off2!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ())))Solve the problem
@time sol = solve(prob, callback=cbs) 14.193066 seconds (41.74 M allocations: 2.047 GiB, 4.49% gc time, 99.99% compilation time)retcode: Success
Interpolation: 3rd order Hermite
t: 182-element Vector{Float64}:
0.0
0.28649552814014345
0.6282062598888134
1.1292780059864103
1.788539543713246
2.7280332499045175
3.8225722202572276
4.8381191258330505
5.700042620198738
6.449974938460642
⋮
83.08550084988944
84.68757283583017
86.36508587463354
87.9411308931485
89.94212068494683
92.62633478311324
95.0183911841383
97.77489387246487
100.0
u: 182-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(v = 1, m = 2, h = 3, n = 4)}}}}:
ComponentVector{Float64}(v = -59.8977, m = 0.0536, h = 0.5925, n = 0.3192)
ComponentVector{Float64}(v = -59.896772589630615, m = 0.053584781785332665, h = 0.592500685682472, n = 0.3192027439091019)
ComponentVector{Float64}(v = -59.896078417587496, m = 0.05358354985022893, h = 0.5925003853539793, n = 0.31920656870895786)
ComponentVector{Float64}(v = -59.895380703866564, m = 0.05358732070491404, h = 0.592498563192231, n = 0.3192127047916002)
ComponentVector{Float64}(v = -59.894827103417214, m = 0.05359154097918554, h = 0.5924946675523771, n = 0.3192210724000593)
ComponentVector{Float64}(v = -59.894615228409705, m = 0.05359428457937094, h = 0.5924881300109393, n = 0.31923235771422587)
ComponentVector{Float64}(v = -59.89505890343335, m = 0.05359755851450737, h = 0.5924816552294706, n = 0.31924307874932606)
ComponentVector{Float64}(v = -59.896269814551104, m = 0.053625090215204584, h = 0.5924780715825779, n = 0.3192501479046132)
ComponentVector{Float64}(v = -59.897715332885426, m = 0.053671317462470676, h = 0.5924772857413374, n = 0.3192539371264494)
ComponentVector{Float64}(v = -59.89809941543937, m = 0.05366424957886711, h = 0.5924790001540866, n = 0.3192552276259311)
⋮
ComponentVector{Float64}(v = -59.572041508381496, m = 0.05528229936041572, h = 0.5998129418239161, n = 0.3140895432023191)
ComponentVector{Float64}(v = -59.3871156498711, m = 0.05680408616439393, h = 0.5959318039144645, n = 0.31711853136160273)
ComponentVector{Float64}(v = -59.461923119094386, m = 0.05653398425720112, h = 0.5922683845153287, n = 0.3196612531516231)
ComponentVector{Float64}(v = -59.65856013055289, m = 0.05531461683057056, h = 0.5902962735663893, n = 0.3208645151692903)
ComponentVector{Float64}(v = -59.892587403978155, m = 0.053755450775810655, h = 0.589915455121986, n = 0.3209066036753039)
ComponentVector{Float64}(v = -60.01730843070407, m = 0.05284271131591328, h = 0.5912762491075266, n = 0.31984145427508204)
ComponentVector{Float64}(v = -59.98358706071466, m = 0.052993705060497186, h = 0.5924921290712457, n = 0.3190531562629898)
ComponentVector{Float64}(v = -59.90819696076022, m = 0.05347090006538309, h = 0.5929547323653732, n = 0.31884981776833593)
ComponentVector{Float64}(v = -59.87503082817752, m = 0.053704873523982434, h = 0.5927942596256218, n = 0.31902538852608303)
Visual
plot(sol.t, sol[1, :], xlabel="Time (ms)", ylabel="Membrane potential (mV)", title="Fig 1.9", label=false, legend=:topleft)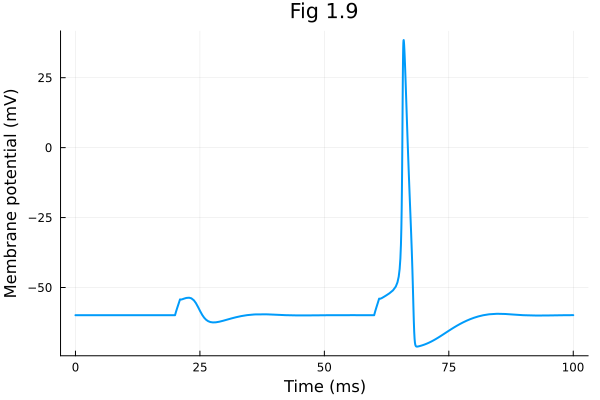
This notebook was generated using Literate.jl.
Back to top