Fig 7.17

Goodwin oscillator model: https://en.wikipedia.org/wiki/Goodwin_model_(biology)

using ComponentArrays
using SimpleUnPack
using OrdinaryDiffEq
using Plots
Plots.default(linewidth=2)
function model717!(D, u, p, t)
    @unpack a, k, b, α, β, γ, δ, n = p
    @unpack X, Y, Z = u
    D.X = a / (k^n + Z^n) - b * X
    D.Y = α * X - β * Y
    D.Z = γ * Y - δ * Z
    nothing
end
model717! (generic function with 1 method)
ps717 = ComponentArray(
    a = 360.0,
    k = 1.368,
    b = 1.0,
    α = 1.0,
    β = 0.6,
    γ = 1.0,
    δ = 0.8,
    n = 12.0
)

u0 = ComponentArray(
    X = 0.0,
    Y = 0.0,
    Z = 0.0
)

tend = 35.0
prob717 = ODEProblem(model717!, u0, tend, ps717)
ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(X = 1, Y = 2, Z = 3)}}} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 35.0)
u0: ComponentVector{Float64}(X = 0.0, Y = 0.0, Z = 0.0)
@time sol = solve(prob717)
 11.657783 seconds (37.73 M allocations: 1.858 GiB, 2.57% gc time, 100.00% compilation time)
retcode: Success
Interpolation: 3rd order Hermite
t: 74-element Vector{Float64}:
  0.0
  9.999999999999999e-5
  0.0010999999999999998
  0.011099999999999997
  0.041561068228358915
  0.08505007717877648
  0.1400425786140992
  0.2146417543721738
  0.31201584322447784
  0.4390615514552524
  ⋮
 30.399216275051014
 31.019732084200392
 31.782434145750724
 32.3743621530088
 32.9240804229318
 33.47916779303648
 33.94226811022297
 34.51649669667564
 35.0
u: 74-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(X = 1, Y = 2, Z = 3)}}}}:
 ComponentVector{Float64}(X = 0.0, Y = 0.0, Z = 0.0)
 ComponentVector{Float64}(X = 0.0008380069445083983, Y = 4.1900207549215655e-8, Z = 1.3966642737483395e-12)
 ComponentVector{Float64}(X = 0.009213468964138544, Y = 5.067222002693897e-6, Z = 1.8578451380267915e-9)
 ComponentVector{Float64}(X = 0.09250904681199522, Y = 0.0005132339779722273, Z = 1.8975593394034844e-6)
 ComponentVector{Float64}(X = 0.34116338821048725, Y = 0.0070794913530376055, Z = 9.780450237545616e-5)
 ComponentVector{Float64}(X = 0.683292323356918, Y = 0.02897046980274338, Z = 0.0008166279287941536)
 ComponentVector{Float64}(X = 1.095152006170422, Y = 0.07629612549303964, Z = 0.0035279811532653834)
 ComponentVector{Float64}(X = 1.6188553354727238, Y = 0.1723356709595111, Z = 0.012150996243756597)
 ComponentVector{Float64}(X = 2.246222895432165, Y = 0.3461133927935709, Z = 0.03523230985115964)
 ComponentVector{Float64}(X = 2.978081158465377, Y = 0.6417560311991968, Z = 0.09109022137495452)
 ⋮
 ComponentVector{Float64}(X = 0.5089918673039764, Y = 1.76678196894839, Z = 2.222822915618968)
 ComponentVector{Float64}(X = 0.28809734163896655, Y = 1.4141811569212321, Z = 2.1240480319262955)
 ComponentVector{Float64}(X = 0.19686438454763533, Y = 1.0306516147476086, Z = 1.8357226708588608)
 ComponentVector{Float64}(X = 0.4107884605856136, Y = 0.8572566168585127, Z = 1.577854680384778)
 ComponentVector{Float64}(X = 1.2775009216741222, Y = 0.9943227874496434, Z = 1.4141809791269315)
 ComponentVector{Float64}(X = 2.091840335870595, Y = 1.5588431984569109, Z = 1.478931229082263)
 ComponentVector{Float64}(X = 1.7685358003391871, Y = 1.9820078566219799, Z = 1.7201935243220492)
 ComponentVector{Float64}(X = 1.077253273369972, Y = 2.0788289937151028, Z = 2.03956986946675)
 ComponentVector{Float64}(X = 0.6803805235209354, Y = 1.914105203829351, Z = 2.1884744444026585)
plot(sol, title="Fig 7.17 (A)", xlabel="Time", ylabel="Concentration", labels=["X" "Y" "Z"])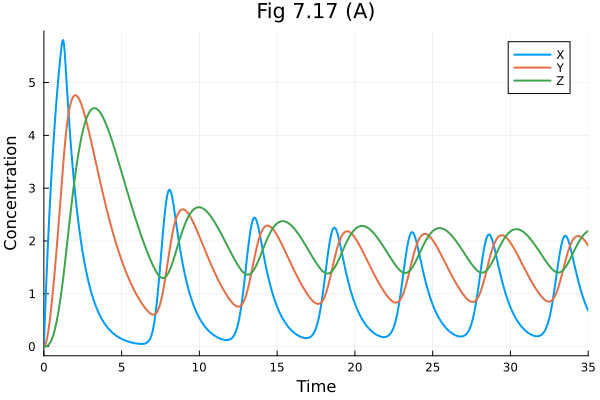

plot(sol, idxs=(1, 2, 3), title="Fig 7.17 (B)", legend=false, size=(600, 600))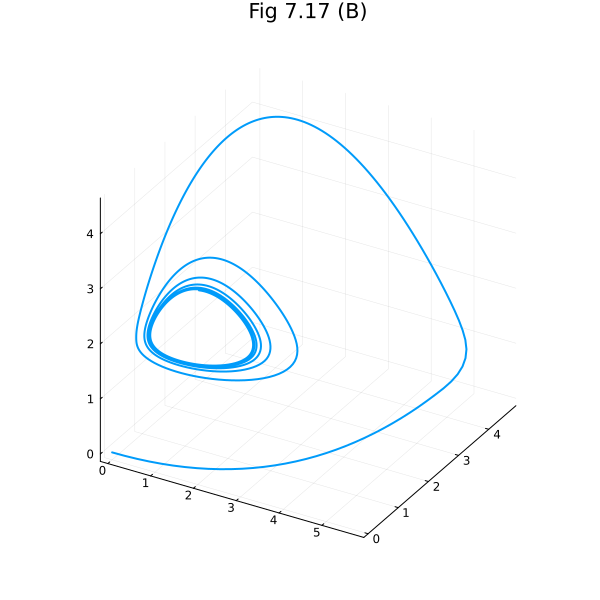

This notebook was generated using Literate.jl.

Back to top