Fig 6.3

Fig 6.3#

Two component pathway

using ModelingToolkit
using Catalyst
using OrdinaryDiffEq
using SteadyStateDiffEq
using Plots
Plots.default(linewidth=2)

rn = @reaction_network begin
    (k1 * L, km1), R <--> RL
    k2, P + RL --> Ps + RL
    k3, Ps--> P
end
\[\begin{split} \begin{align*} \mathrm{R} &\xrightleftharpoons[\mathtt{km1}]{L \mathtt{k1}} \mathrm{\mathtt{RL}} \\ \mathrm{P} + \mathrm{\mathtt{RL}} &\xrightarrow{\mathtt{k2}} \mathrm{\mathtt{Ps}} + \mathrm{\mathtt{RL}} \\ \mathrm{\mathtt{Ps}} &\xrightarrow{\mathtt{k3}} \mathrm{P} \end{align*} \end{split}\]
setdefaults!(rn, [
    :R => 3.,
    :RL => 0.,
    :P => 8.0,
    :Ps => 0.,
    :L => 0.,
    :k1 => 5.,
    :km1 => 1.,
    :k2 => 6.,
    :k3 => 2.,
])

@independent_variables t
@unpack L = rn
discrete_events = [[1.0] => [L~3.0], [3.0] => [L~0.0]]

osys = convert(ODESystem, rn; discrete_events, remove_conserved = true) |> structural_simplify
\[\begin{split} \begin{align} \frac{\mathrm{d} P\left( t \right)}{\mathrm{d}t} &= \mathtt{k3} \left( - P\left( t \right) + \Gamma_{2} \right) - \mathtt{k2} \left( - R\left( t \right) + \Gamma_{1} \right) P\left( t \right) \\ \frac{\mathrm{d} R\left( t \right)}{\mathrm{d}t} &= \mathtt{km1} \left( - R\left( t \right) + \Gamma_{1} \right) - L \mathtt{k1} R\left( t \right) \end{align} \end{split}\]
equations(osys)
\[\begin{split} \begin{align} \frac{\mathrm{d} P\left( t \right)}{\mathrm{d}t} &= \mathtt{k3} \left( - P\left( t \right) + \Gamma_{2} \right) - \mathtt{k2} \left( - R\left( t \right) + \Gamma_{1} \right) P\left( t \right) \\ \frac{\mathrm{d} R\left( t \right)}{\mathrm{d}t} &= \mathtt{km1} \left( - R\left( t \right) + \Gamma_{1} \right) - L \mathtt{k1} R\left( t \right) \end{align} \end{split}\]

Fig. 6.3 A#

tspan = (0., 10.)
prob = ODEProblem(osys, [], tspan, [])
sol = solve(prob)

retcode: Success
Interpolation: 3rd order Hermite
t: 51-element Vector{Float64}:
  0.0
  9.999999999999999e-5
  0.0010999999999999998
  0.011099999999999997
  0.11109999999999996
  1.0
  1.0
  1.0463687845335854
  1.0687821871454328
  1.110257175110315
  ⋮
  5.717160539667416
  6.1011479186475315
  6.5290797493093065
  7.006355545327002
  7.540553625680684
  8.142549043858686
  8.828818546386866
  9.625182680128827
 10.0
u: 51-element Vector{Vector{Float64}}:
 [8.0, 3.0]
 [8.0, 3.0]
 [8.0, 3.0]
 [8.0, 3.0]
 [8.0, 3.0]
 [8.0, 3.0]
 [8.0, 3.0]
 [6.408338177835751, 1.5269184341495876]
 [5.196367770807921, 1.1232765241899916]
 [3.3076095645766563, 0.669432573214865]
 ⋮
 [4.585874519631833, 2.8142005246723847]
 [5.222764915894305, 2.87344447186153]
 [5.859931006576904, 2.9175039423599265]
 [6.454538443292145, 2.948813427740215]
 [6.966562707384316, 2.969997376980437]
 [7.368960043804991, 2.9835668143490177]
 [7.654328099232809, 2.991726411815315]
 [7.834374287877937, 2.996268501614989]
 [7.883912265610946, 2.9974349114353545]

@unpack RL, Ps = osys
fig = plot(sol, idxs=[RL, Ps], labels= ["RL" "P*"])
plot!(fig, t -> 3 * (1<=t<=3), label="Ligand", line=(:black, :dash), linealpha=0.7)
plot!(fig, title="Fig. 6.3 (A)", xlabel="Time", ylabel="Concentration")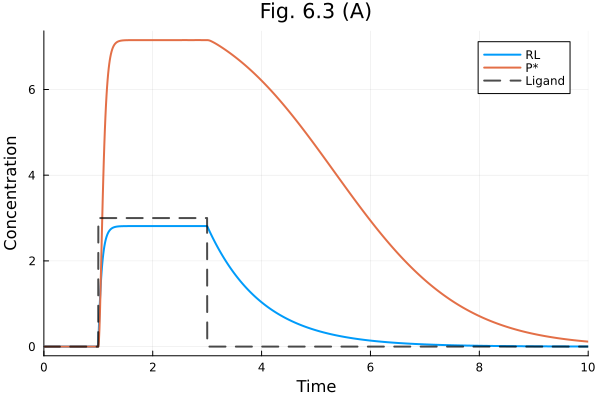
../_images/9269f95337bf7112ce8d7f6b6eab300b65cde0fdb13551cfaebd00a8ca5152d0.png

Fig 6.3 B#

@unpack RL, Ps = osys
lrange = 0:0.01:1

prob_func = (prob, i, repeat) -> remake(prob, p=[L => lrange[i]])
prob = SteadyStateProblem(osys, [], [])
trajectories = length(lrange)
alg = DynamicSS(Rodas5())
eprob = EnsembleProblem(prob; prob_func)
sim = solve(eprob, alg; trajectories, abstol=1e-10, reltol=1e-10)

pstar = map(s->s[Ps], sim)
rl = map(s->s[RL], sim)
plot(lrange, [pstar rl], label=["P*" "RL"], title="Fig. 6.3 (B)",
xlabel="Ligand", ylabel="Steady-state concentration", xlims=(0, 1), ylims=(0, 8))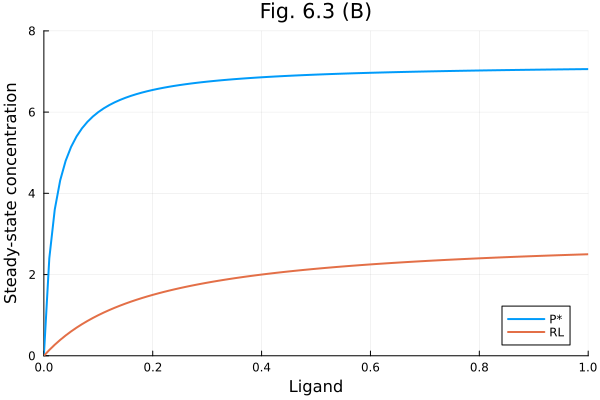
../_images/cc5bb60a3ca6dce29fedc7d81b0376cb42ba035cc5cb5d965519eef7aa378560.png

This notebook was generated using Literate.jl.

Contents