using OrdinaryDiffEq
using ModelingToolkit
using Plots
Plots.default(linewidth=2)Fig 7.11
Model of phage lambda decision switch
Model
function build_model_711(;name)
@independent_variables t
D = Differential(t)
@variables r(t) = 0.0 c(t) = 0.0
@parameters begin
K1=1
K2=0.1
K3=5
K4=0.5
delta_r=0.02
delta_c=0.02
a=5
b=50
end
rd = r / 2
cd = c / 2
f1 = K1 * rd^2
f2 = K2 * rd
f3 = K3 * cd
f4 = K4 * cd
den = 1 + f1 * (1 + f2) + f3 * (1 + f4)
eqs = [
D(r) ~ a * (1 + 10 * f1) / den - delta_r * r,
D(c) ~ b * (1 + f3) / den - delta_c * c
]
return ODESystem(eqs, t; name)
end
@mtkbuild sys = build_model_711()\[ \begin{align} \frac{\mathrm{d} c\left( t \right)}{\mathrm{d}t} &= \frac{\left( 1 + \frac{1}{2} \mathtt{K3} c\left( t \right) \right) b}{1 + \frac{1}{2} \mathtt{K3} \left( 1 + \frac{1}{2} \mathtt{K4} c\left( t \right) \right) c\left( t \right) + \frac{1}{4} \left( r\left( t \right) \right)^{2} \mathtt{K1} \left( 1 + \frac{1}{2} \mathtt{K2} r\left( t \right) \right)} - \mathtt{delta\_c} c\left( t \right) \\ \frac{\mathrm{d} r\left( t \right)}{\mathrm{d}t} &= \frac{\left( 1 + \frac{5}{2} \left( r\left( t \right) \right)^{2} \mathtt{K1} \right) a}{1 + \frac{1}{2} \mathtt{K3} \left( 1 + \frac{1}{2} \mathtt{K4} c\left( t \right) \right) c\left( t \right) + \frac{1}{4} \left( r\left( t \right) \right)^{2} \mathtt{K1} \left( 1 + \frac{1}{2} \mathtt{K2} r\left( t \right) \right)} - \mathtt{delta\_r} r\left( t \right) \end{align} \]
Fig 7.11 (A)
tend = 6000.0
prob = ODEProblem(sys, [], tend)
∂R = (x, y) -> prob.f([x, y], prob.p, nothing)[1]
∂C = (x, y) -> prob.f([x, y], prob.p, nothing)[2]
∂F = function (x, y; scale=0.2)
dR, dC = prob.f([x, y], prob.p, nothing)
s = sqrt(hypot(dR, dC)) * scale
return (dR / s, dC / s)
end
rx = range(0, 250, 201)
ry = range(0, 250, 201)
rxy = range(0, 250, 21)
xx = [x for y in rxy, x in rxy]
yy = [y for y in rxy, x in rxy]
fig = plot(title="Figure 7.11 (A)")
contour!(fig, rx, ry, ∂R, levels=[0], cbar=false, line=(:black))
plot!(fig, Float64[], Float64[], line=(:black), label="R nullcline")
contour!(fig, rx, ry, ∂C, levels=[0], cbar=false, line=(:black, :dash))
plot!(fig, Float64[], Float64[], line=(:black, :dash), label="C nullcline")
quiver!(fig, xx, yy, quiver=∂F, line=(:lightblue), arrow=(:closed))
plot!(fig, xlims=(0, 250), ylims=(0, 250), xlabel="[cI] (nM)", ylabel="[cro] (nM)", aspect_ratio=:equal, legend=:top, size=(600, 600))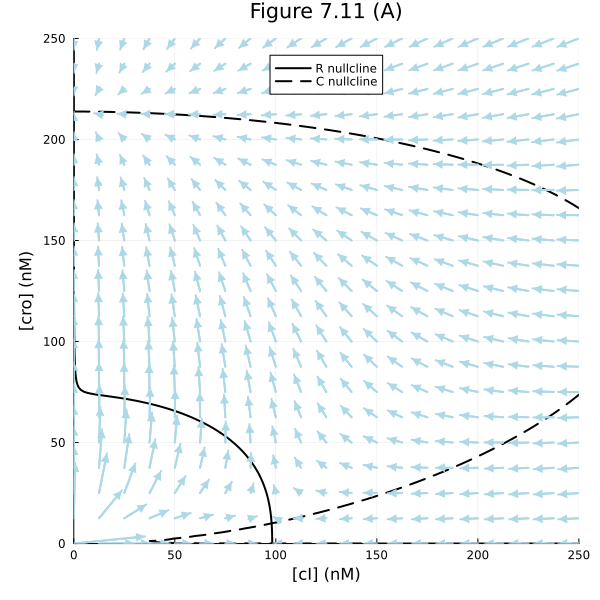
Fig 7.11 (B)
prob2 = remake(prob, p = [sys.delta_r => 0.2])
rx = range(0, 250, 201)
ry = range(0, 250, 201)
rxy = range(0, 250, 21)
xx = [x for y in rxy, x in rxy]
yy = [y for y in rxy, x in rxy]
∂R2 = (x, y) -> prob2.f([x, y], prob2.p, nothing)[1]
∂C2 = (x, y) -> prob2.f([x, y], prob2.p, nothing)[2]
∂F2 = function (x, y; scale=0.2)
dR, dC = prob2.f([x, y], prob2.p, nothing)
s = sqrt(hypot(dR, dC)) * scale
return (dR / s, dC / s)
end
fig = plot(title="Figure 7.11 (B)")
contour!(fig, rx, ry, ∂R2, levels=[0], cbar=false, line=(:black))
plot!(fig, Float64[], Float64[], line=(:black), label="R nullcline")
contour!(fig, rx, ry, ∂C2, levels=[0], cbar=false, line=(:black, :dash))
plot!(fig, Float64[], Float64[], line=(:black, :dash), label="C nullcline")
quiver!(fig, xx, yy, quiver=∂F2, line=(:lightblue), arrow=(:closed))
plot!(fig, xlims=(0, 250), ylims=(0, 250), xlabel="[cI] (nM)", ylabel="[cro] (nM)", aspect_ratio=:equal, legend=:top, size=(600, 600))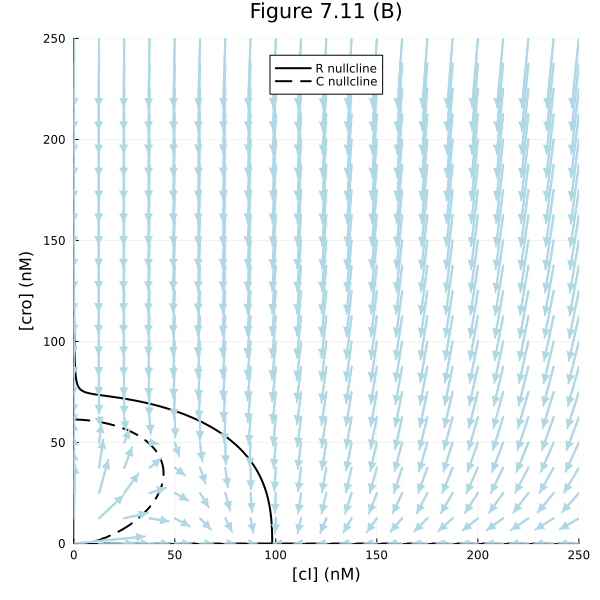
This notebook was generated using Literate.jl.