using OrdinaryDiffEq
using DiffEqCallbacks
using ComponentArrays
using Plots
Plots.default(linewidth=2)Fig 1.7
For Figures 1.7, 7.13, 7.14, 7.15.
Convenience functions
hil(x, k) = x / (x + k)
hil(x, k, n) = hil(x^n, k^n)hil (generic function with 2 methods)Collins toggle switch model
function collins!(du, u, p, t)
a1, a2, β, γ, i1, i2 = p
s1, s2 = u
du[1] = a1 * hil(1 + i2, s2, β) - s1
du[2] = a2 * hil(1 + i1, s1, γ) - s2
nothing
endcollins! (generic function with 1 method)Setup the problem
tspan = (0.0, 50.0)
ps = [3.0, 2.5, 4.0, 4.0, 0.0, 0.0] # a1, a2, β, γ, i1, i2
u0 = [0.075, 2.5] # s1, s2
prob = ODEProblem(collins!, u0, tspan, ps)ODEProblem with uType Vector{Float64} and tType Float64. In-place: true Non-trivial mass matrix: false timespan: (0.0, 50.0) u0: 2-element Vector{Float64}: 0.075 2.5
Callbacks
affect_i2_on!(integrator) = integrator.p[6] = 10.0
affect_i2_off!(integrator) = integrator.p[6] = 0.0
affect_i1_on!(integrator) = integrator.p[5] = 10.0
affect_i1_off!(integrator) = integrator.p[5] = 0.0
cb_i2_on = PresetTimeCallback(10.0, affect_i2_on!)
cb_i2_off = PresetTimeCallback(20.0, affect_i2_off!)
cb_i1_on = PresetTimeCallback(30.0, affect_i1_on!)
cb_i1_off = PresetTimeCallback(40.0, affect_i1_off!)
cbs = CallbackSet(cb_i2_on, cb_i2_off, cb_i1_on, cb_i1_off)SciMLBase.CallbackSet{Tuple{}, Tuple{SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_on!)}, typeof(Main.var"##283".affect_i2_on!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_on!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_off!)}, typeof(Main.var"##283".affect_i2_off!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_off!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_on!)}, typeof(Main.var"##283".affect_i1_on!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_on!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_off!)}, typeof(Main.var"##283".affect_i1_off!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_off!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}}}((), (SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_on!)}, typeof(Main.var"##283".affect_i2_on!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_on!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_on!)}([10.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i2_on!), Main.var"##283".affect_i2_on!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_on!)}([10.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i2_on!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_off!)}, typeof(Main.var"##283".affect_i2_off!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_off!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_off!)}([20.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i2_off!), Main.var"##283".affect_i2_off!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i2_off!)}([20.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i2_off!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_on!)}, typeof(Main.var"##283".affect_i1_on!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_on!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_on!)}([30.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i1_on!), Main.var"##283".affect_i1_on!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_on!)}([30.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i1_on!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_off!)}, typeof(Main.var"##283".affect_i1_off!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_off!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_off!)}([40.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i1_off!), Main.var"##283".affect_i1_off!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##283".affect_i1_off!)}([40.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##283".affect_i1_off!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ())))Solve the problem
@time sol = solve(prob, callback=cbs) 6.155512 seconds (17.89 M allocations: 919.428 MiB, 2.26% gc time, 99.98% compilation time)retcode: Success
Interpolation: 3rd order Hermite
t: 45-element Vector{Float64}:
0.0
0.38548049109061366
1.2786313586853497
2.464538731594535
4.06089298356771
6.199065127274195
9.163107137014421
10.0
10.0
10.90492160678711
⋮
37.811045850454185
38.97117380017039
40.0
40.0
41.45655048835799
43.01214443871626
45.107570048628844
47.65220584313297
50.0
u: 45-element Vector{Vector{Float64}}:
[0.075, 2.5]
[0.07496310584167308, 2.4999747263084022]
[0.0749189538414308, 2.499943104158718]
[0.0748994736010588, 2.49992797574084]
[0.07489347508722315, 2.4999227222886917]
[0.07489238103870041, 2.4999215657222047]
[0.07489230549277733, 2.4999214349680683]
[0.07489223296465886, 2.49992138933308]
[0.07489223296465886, 2.49992138933308]
[1.8138876963707786, 1.6074955381407825]
⋮
[0.07794218751213773, 2.498990428766632]
[0.07588614749855138, 2.499682949330218]
[0.0752553715213293, 2.4998865900140177]
[0.0752553715213293, 2.4998865900140177]
[0.07497917389522026, 2.4999126610145854]
[0.07491123383177441, 2.499919371700559]
[0.07489514451004411, 2.4999210438808794]
[0.07489273938700679, 2.499921301318458]
[0.07489227301035209, 2.4999213465656758]Visual
plot(sol, legend=:right, xlabel = "Time", ylabel="Concentration", title="Fig 1.7", labels=["s1" "s2"])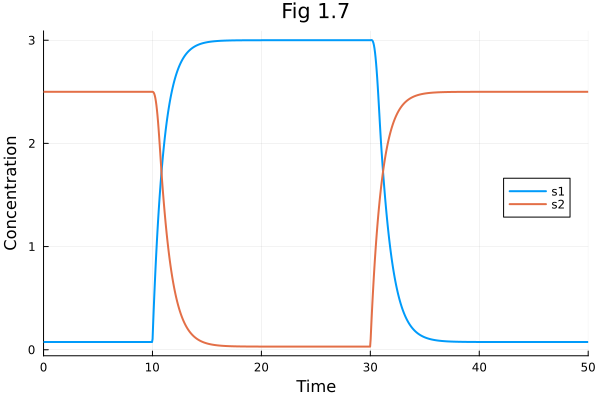
This notebook was generated using Literate.jl.
Back to top