Fig 6.16

Model of apoptosis signalling pathway

using Catalyst
using ModelingToolkit
using DifferentialEquations
using Plots
Plots.default(linewidth=2)

rn = @reaction_network begin
    @parameters I(t)
    (k1, k2), 0 <--> C8
    k3 * (C3s + I), C8 --> C8s
    k4, C8s --> 0
    (k5, k6), C8s + BAR <--> C8sBAR
    (k7, k8), 0 <--> C3
    k9 * C8s, C3 --> C3s
    k10, C3s --> 0
    (k11, k12), C3s + IAP <--> C3sIAP
    (k13, k14), 0 <--> BAR
    (k15, k16 + k17 * C3s), 0 <--> IAP
    k18, C8sBAR --> 0
    k19, C3sIAP --> 0
end

\[\begin{split} \begin{align*} \varnothing &\xrightleftharpoons[\mathtt{k2}]{\mathtt{k1}} \mathrm{\mathtt{C8}} \\ \mathrm{\mathtt{C8}} &\xrightarrow{\left( \mathtt{C3s} + I\left( t \right) \right) \mathtt{k3}} \mathrm{\mathtt{C8s}} \\ \mathrm{\mathtt{C8s}} &\xrightarrow{\mathtt{k4}} \varnothing \\ \mathrm{\mathtt{C8s}} + \mathrm{\mathtt{BAR}} &\xrightleftharpoons[\mathtt{k6}]{\mathtt{k5}} \mathrm{\mathtt{C8sBAR}} \\ \varnothing &\xrightleftharpoons[\mathtt{k8}]{\mathtt{k7}} \mathrm{\mathtt{C3}} \\ \mathrm{\mathtt{C3}} &\xrightarrow{\mathtt{C8s} \mathtt{k9}} \mathrm{\mathtt{C3s}} \\ \mathrm{\mathtt{C3s}} &\xrightarrow{\mathtt{k10}} \varnothing \\ \mathrm{\mathtt{C3s}} + \mathrm{\mathtt{IAP}} &\xrightleftharpoons[\mathtt{k12}]{\mathtt{k11}} \mathrm{\mathtt{C3sIAP}} \\ \varnothing &\xrightleftharpoons[\mathtt{k14}]{\mathtt{k13}} \mathrm{\mathtt{BAR}} \\ \varnothing &\xrightleftharpoons[\mathtt{k16} + \mathtt{C3s} \mathtt{k17}]{\mathtt{k15}} \mathrm{\mathtt{IAP}} \\ \mathrm{\mathtt{C8sBAR}} &\xrightarrow{\mathtt{k18}} \varnothing \\ \mathrm{\mathtt{C3sIAP}} &\xrightarrow{\mathtt{k19}} \varnothing \end{align*} \end{split}\]

setdefaults!(rn, [
    :k1 => 507,
    :k2 => 3.9e-3,
    :k3 => 1e-5,
    :k4 => 5.8e-3,
    :k5 => 5e-4,
    :k6 => 0.21,
    :k7 => 81.9,
    :k8 => 3.9e-3,
    :k9 => 5.8e-6,
    :k10 => 5.8e-3,
    :k11 => 5e-4,
    :k12 => 0.21,
    :k13 => 40,
    :k14 => 1e-3,
    :k15 => 464,
    :k16 => 1.16e-2,
    :k17 => 3e-4,
    :k18 => 1.16e-2,
    :k19 => 1.73e-2,
    :I => 0.0,
    :C8 => 1.3E5,
    :C8s => 0.0,
    :C3 => 0.21E5,
    :C3s => 0.0,
    :BAR => 0.4E5,
    :IAP => 0.4E5,
    :C8sBAR => 0.0,
    :C3sIAP => 0.0
])

@unpack I = rn

osys = convert(ODESystem, rn; remove_conserved = true, discrete_events = [[100] => [I ~ 200], [1200] => [I ~ 0]]) |> structural_simplify
equations(osys)

┌ Warning: You are creating a system or problem while eliminating conserved quantities. Please note,
│         due to limitations / design choices in ModelingToolkit if you use the created system to
│         create a problem (e.g. an `ODEProblem`), or are directly creating a problem, you *should not*
│         modify that problem's initial conditions for species (e.g. using `remake`). Changing initial
│         conditions must be done by creating a new Problem from your reaction system or the
│         ModelingToolkit system you converted it into with the new initial condition map.
│         Modification of parameter values is still possible, *except* for the modification of any
│         conservation law constants (Γ), which is not possible. You might
│         get this warning when creating a problem directly.
│ 
│         You can remove this warning by setting `remove_conserved_warn = false`.
└ @ Catalyst ~/.julia/packages/Catalyst/48wH3/src/reactionsystem_conversions.jl:456

\[\begin{split} \begin{align} \frac{\mathrm{d} \mathtt{C8}\left( t \right)}{\mathrm{d}t} &= \mathtt{k1} - \mathtt{k2} \mathtt{C8}\left( t \right) - \mathtt{k3} \mathtt{C8}\left( t \right) \left( \mathtt{C3s}\left( t \right) + I\left( t \right) \right) \\ \frac{\mathrm{d} \mathtt{C8s}\left( t \right)}{\mathrm{d}t} &= - \mathtt{k4} \mathtt{C8s}\left( t \right) + \mathtt{k6} \mathtt{C8sBAR}\left( t \right) + \mathtt{k3} \mathtt{C8}\left( t \right) \left( \mathtt{C3s}\left( t \right) + I\left( t \right) \right) - \mathtt{k5} \mathtt{BAR}\left( t \right) \mathtt{C8s}\left( t \right) \\ \frac{\mathrm{d} \mathtt{BAR}\left( t \right)}{\mathrm{d}t} &= \mathtt{k13} - \mathtt{k14} \mathtt{BAR}\left( t \right) + \mathtt{k6} \mathtt{C8sBAR}\left( t \right) - \mathtt{k5} \mathtt{BAR}\left( t \right) \mathtt{C8s}\left( t \right) \\ \frac{\mathrm{d} \mathtt{C8sBAR}\left( t \right)}{\mathrm{d}t} &= - \mathtt{k18} \mathtt{C8sBAR}\left( t \right) - \mathtt{k6} \mathtt{C8sBAR}\left( t \right) + \mathtt{k5} \mathtt{BAR}\left( t \right) \mathtt{C8s}\left( t \right) \\ \frac{\mathrm{d} \mathtt{C3}\left( t \right)}{\mathrm{d}t} &= \mathtt{k7} - \mathtt{k8} \mathtt{C3}\left( t \right) - \mathtt{k9} \mathtt{C8s}\left( t \right) \mathtt{C3}\left( t \right) \\ \frac{\mathrm{d} \mathtt{C3s}\left( t \right)}{\mathrm{d}t} &= - \mathtt{k10} \mathtt{C3s}\left( t \right) + \mathtt{k12} \mathtt{C3sIAP}\left( t \right) - \mathtt{k11} \mathtt{C3s}\left( t \right) \mathtt{IAP}\left( t \right) + \mathtt{k9} \mathtt{C8s}\left( t \right) \mathtt{C3}\left( t \right) \\ \frac{\mathrm{d} \mathtt{IAP}\left( t \right)}{\mathrm{d}t} &= \mathtt{k15} + \mathtt{k12} \mathtt{C3sIAP}\left( t \right) - \mathtt{k11} \mathtt{C3s}\left( t \right) \mathtt{IAP}\left( t \right) + \left( - \mathtt{k16} - \mathtt{k17} \mathtt{C3s}\left( t \right) \right) \mathtt{IAP}\left( t \right) \\ \frac{\mathrm{d} \mathtt{C3sIAP}\left( t \right)}{\mathrm{d}t} &= - \mathtt{k12} \mathtt{C3sIAP}\left( t \right) - \mathtt{k19} \mathtt{C3sIAP}\left( t \right) + \mathtt{k11} \mathtt{C3s}\left( t \right) \mathtt{IAP}\left( t \right) \end{align} \end{split}\]

tspan = (0., 1800.)
prob = ODEProblem(osys, [], (0., 1800.))

ODEProblem with uType Vector{Float64} and tType Float64. In-place: true
timespan: (0.0, 1800.0)
u0: 8-element Vector{Float64}:
 130000.0
      0.0
  40000.0
      0.0
  21000.0
      0.0
  40000.0
      0.0

sol = solve(prob)

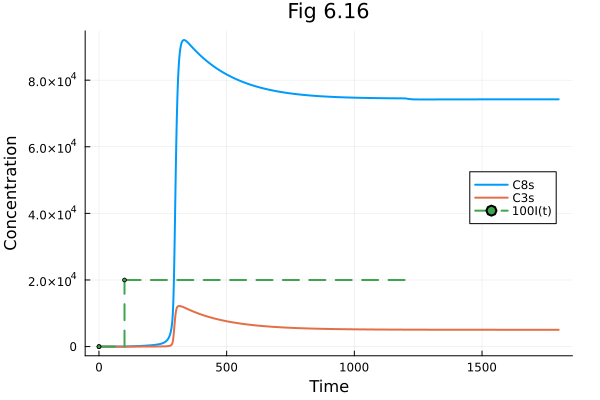
plot(sol, idxs=[osys.C8s, osys.C3s, I*100], title="Fig 6.16", xlabel="Time", ylabel="Concentration", legend=:right, rightmargin=5*Plots.mm)

---

This notebook was generated using Literate.jl.