Fig 2.09

Metabolic network simulation

Using Catalyst.jl to simulate a metabolic network.

using DifferentialEquations
using Catalyst
using ModelingToolkit
using Plots
Plots.default(linewidth=2)

rn = @reaction_network begin
    k1, 0 --> A
    k2, A --> B
    k3, A + B --> C + D
    k4, C --> 0
    k5, D --> 0
end

\[\begin{split} \begin{align*} \varnothing &\xrightarrow{\mathtt{k1}} \mathrm{A} \\ \mathrm{A} &\xrightarrow{\mathtt{k2}} \mathrm{B} \\ \mathrm{A} + \mathrm{B} &\xrightarrow{\mathtt{k3}} \mathrm{C} + \mathrm{D} \\ \mathrm{C} &\xrightarrow{\mathtt{k4}} \varnothing \\ \mathrm{D} &\xrightarrow{\mathtt{k5}} \varnothing \end{align*} \end{split}\]

Showing the differential equations in the reaction network

osys = convert(ODESystem, rn) |> complete
equations(osys)

\[\begin{split} \begin{align} \frac{\mathrm{d} A\left( t \right)}{\mathrm{d}t} &= \mathtt{k1} - \mathtt{k2} A\left( t \right) - \mathtt{k3} B\left( t \right) A\left( t \right) \\ \frac{\mathrm{d} B\left( t \right)}{\mathrm{d}t} &= \mathtt{k2} A\left( t \right) - \mathtt{k3} B\left( t \right) A\left( t \right) \\ \frac{\mathrm{d} C\left( t \right)}{\mathrm{d}t} &= - \mathtt{k4} C\left( t \right) + \mathtt{k3} B\left( t \right) A\left( t \right) \\ \frac{\mathrm{d} D\left( t \right)}{\mathrm{d}t} &= - \mathtt{k5} D\left( t \right) + \mathtt{k3} B\left( t \right) A\left( t \right) \end{align} \end{split}\]

Solve the problem

ps = [:k1=>3., :k2=>2., :k3=>2.5, :k4=>3., :k5=>4.]
u0 = [:A=>0., :B=>0., :C=>0., :D=>0.]
tend = 10.
prob = ODEProblem(osys, u0, tend, ps)
sol = solve(prob)

retcode: Success
Interpolation: 3rd order Hermite
t: 31-element Vector{Float64}:
  0.0
  9.999999999999999e-5
  0.0010999999999999998
  0.011099999999999997
  0.03427453254462915
  0.06522753353833287
  0.10153577459409753
  0.14533869701822555
  0.19788890020410435
  0.2619461233746949
  ⋮
  3.481141518838101
  4.1462374627542244
  4.984641398737613
  5.978883857784344
  6.9999177726334345
  7.954887766924096
  8.836082624890851
  9.672663483036162
 10.0
u: 31-element Vector{Vector{Float64}}:
 [0.0, 0.0, 0.0, 0.0]
 [0.00029997000199933764, 2.999799953754866e-8, 5.623912546644786e-16, 5.623800072204464e-16]
 [0.003296372652316679, 3.627331236355826e-6, 8.21805646090172e-12, 8.216249166279005e-12]
 [0.0329330063952576, 0.00036682535223159696, 8.356768013816538e-8, 8.338285321893432e-8]
 [0.09937122761544223, 0.0034375565665459152, 7.255794159499436e-6, 7.2066185248634404e-6]
 [0.1833655969433656, 0.01213116604059312, 8.93425388002502e-5, 8.820117939513288e-5]
 [0.2751746900149442, 0.02839992448709784, 0.0004856662162730563, 0.0004761071298392577]
 [0.37646083724449214, 0.055514839373642884, 0.0018497945329364433, 0.0017982532908780546]
 [0.4844196905527861, 0.0965602973248322, 0.005620960526037499, 0.0054101243611241]
 [0.5961814643349723, 0.15505310630069286, 0.014714875647080208, 0.013992428397168613]
 ⋮
 [0.7510154814517538, 0.7988628794584905, 0.49983459077320175, 0.3749491570841432]
 [0.7502915599254344, 0.799672457748166, 0.4999584903912881, 0.37498115400855286]
 [0.7500631110964762, 0.7999305208686217, 0.49998878382839607, 0.37498954873657114]
 [0.7500144275982004, 0.7999882359844379, 0.49999045642132917, 0.37497086078229797]
 [0.750012525058094, 0.7999980647430991, 0.49997804770113236, 0.37488837441788153]
 [0.7500190130496581, 0.799999656046552, 0.4999625081714902, 0.3747465332743503]
 [0.7500193831308752, 0.7999999319182711, 0.4999613387386634, 0.3746770632489783]
 [0.7500144341539162, 0.7999999855119397, 0.49997115427246785, 0.37471457052264967]
 [0.7500039199737636, 0.7999999921573422, 0.49999217253664263, 0.3749250363648064]

Visual

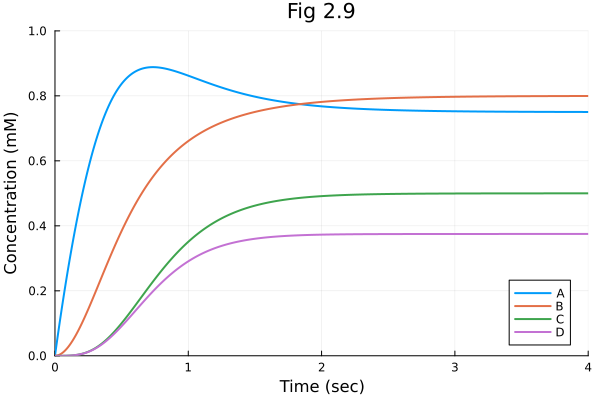
plot(sol, legend=:bottomright, title="Fig 2.9",
    xlims=(0., 4.), ylims=(0., 1.),
    xlabel="Time (sec)", ylabel="Concentration (mM)"
)

---

This notebook was generated using Literate.jl.