Fig 6.5

Contents

Fig 6.5#

Model of G-protein signalling pathway

using ModelingToolkit
using Catalyst
using DifferentialEquations
using Plots
Plots.default(linewidth=2)

rn = @reaction_network begin
    @parameters L(t)
    (kRL * L, kRLm), R <--> RL
    kGa, G + RL --> Ga + Gbg + RL
    kGd0, Ga --> Gd
    kG1, Gd + Gbg --> G
end
\[\begin{split} \begin{align*} \mathrm{R} &\xrightleftharpoons[\mathtt{kRLm}]{\mathtt{kRL} L\left( t \right)} \mathrm{\mathtt{RL}} \\ \mathrm{G} + \mathrm{\mathtt{RL}} &\xrightarrow{\mathtt{kGa}} \mathrm{\mathtt{Ga}} + \mathrm{\mathtt{Gbg}} + \mathrm{\mathtt{RL}} \\ \mathrm{\mathtt{Ga}} &\xrightarrow{\mathtt{kGd0}} \mathrm{\mathtt{Gd}} \\ \mathrm{\mathtt{Gd}} + \mathrm{\mathtt{Gbg}} &\xrightarrow{\mathtt{kG1}} \mathrm{G} \end{align*} \end{split}\]
setdefaults!(rn, [
    :kRL => 2e6,
    :kRLm => 0.01,
    :kGa => 1e-5,
    :kGd0 => 0.11,
    :kG1 => 1,
    :R => 4e3,
    :RL => 0.,
    :G => 1e4,
    :Ga => 0.,
    :Gd => 0.,
    :Gbg => 0.,
    :L => 0.
])

@unpack L = rn
discrete_events = [[200] => [L~1e-9], [800] => [L~0.0]]
osys = convert(ODESystem, rn; discrete_events, remove_conserved = true) |> structural_simplify

┌ Warning: You are creating a system or problem while eliminating conserved quantities. Please note,
│         due to limitations / design choices in ModelingToolkit if you use the created system to
│         create a problem (e.g. an `ODEProblem`), or are directly creating a problem, you *should not*
│         modify that problem's initial conditions for species (e.g. using `remake`). Changing initial
│         conditions must be done by creating a new Problem from your reaction system or the
│         ModelingToolkit system you converted it into with the new initial condition map.
│         Modification of parameter values is still possible, *except* for the modification of any
│         conservation law constants (Γ), which is not possible. You might
│         get this warning when creating a problem directly.
│ 
│         You can remove this warning by setting `remove_conserved_warn = false`.
└ @ Catalyst ~/.julia/packages/Catalyst/48wH3/src/reactionsystem_conversions.jl:456
\[\begin{split} \begin{align} \frac{\mathrm{d} R\left( t \right)}{\mathrm{d}t} &= \mathtt{kRLm} \left( - R\left( t \right) + \Gamma_{1} \right) - \mathtt{kRL} R\left( t \right) L\left( t \right) \\ \frac{\mathrm{d} G\left( t \right)}{\mathrm{d}t} &= \mathtt{kG1} \left( - G\left( t \right) + \Gamma_{2} \right) \left( - G\left( t \right) - \mathtt{Ga}\left( t \right) + \Gamma_{3} \right) - \mathtt{kGa} \left( - R\left( t \right) + \Gamma_{1} \right) G\left( t \right) \\ \frac{\mathrm{d} \mathtt{Ga}\left( t \right)}{\mathrm{d}t} &= - \mathtt{kGd0} \mathtt{Ga}\left( t \right) + \mathtt{kGa} \left( - R\left( t \right) + \Gamma_{1} \right) G\left( t \right) \end{align} \end{split}\]

Fig 6.5 A#

tend = 1200.0
prob = ODEProblem(osys, [], tend)

sol = solve(prob, Rodas5P(), abstol=1e-8, reltol=1e-8)

@unpack RL, Ga = osys
plot(sol, idxs=[RL, Ga], title="Fig 6.05 (A)", xlabel="Time", ylabel="Abundance")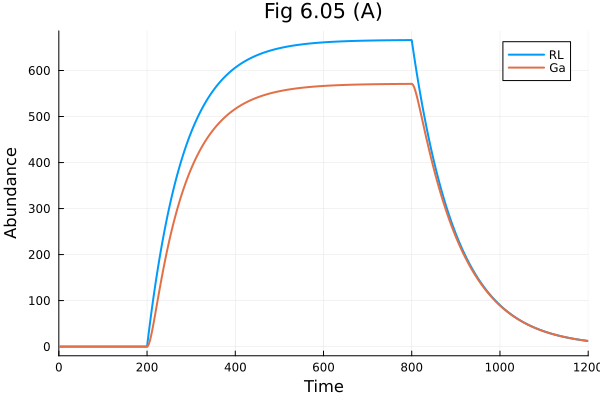

┌ Warning: Initialization system is overdetermined. 3 equations for 0 unknowns. Initialization will default to using least squares. `SCCNonlinearProblem` can only be used for initialization of fully determined systems and hence will not be used here. To suppress this warning pass warn_initialize_determined = false. To make this warning into an error, pass fully_determined = true
└ @ ModelingToolkit ~/.julia/packages/ModelingToolkit/klLLV/src/systems/diffeqs/abstractodesystem.jl:1354
../_images/30d362be789dc3fff440164a5274538b58bb7d09ef977df42130ab17c0ecbc18.png

Fig 6.5 B#

lrange = range(0, 20 * 1e-9, 101)

prob_func = (prob, i, repeat) -> remake(prob, p=[L => lrange[i]])
prob = SteadyStateProblem(osys, [], [])
trajectories = length(lrange)
alg = DynamicSS(Rodas5())
eprob = EnsembleProblem(prob; prob_func)
sim = solve(eprob, alg; trajectories, abstol=1e-10, reltol=1e-10)

ga = map(s->s[Ga], sim)
rl = map(s->s[RL], sim)
plot(lrange .* 1e9, [ga rl], label=["Ga" "RL"], title="Fig. 6.5 (B)",
xlabel="Ligand (nM)", ylabel="Steady-state abundance", xlims=(0, 20), ylims=(0, 3500))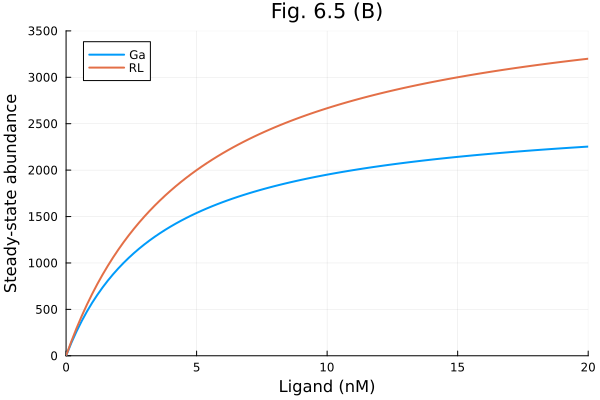
../_images/6d041fd8b1c6c93d3fc6b3fcdc667f900b65a60cf767fe7a8d492ee83f0d3efd.png

This notebook was generated using Literate.jl.

Contents