using OrdinaryDiffEq
using ComponentArrays
using SimpleUnPack
using Plots
Plots.default(linewidth=2)Fig 7.21
repressilator model
function model721!(D, u, p, t)
@unpack α, α0, n, β = p
@unpack mA, mB, mC, A, B, C = u
D.mA = α / (1 + C^n) + α0 - mA
D.mB = α / (1 + A^n) + α0 - mB
D.mC = α / (1 + B^n) + α0 - mC
D.A = β * (mA - A)
D.B = β * (mB - B)
D.C = β * (mC - C)
nothing
endmodel721! (generic function with 1 method)ps721 = ComponentArray(
α = 298.2,
α0 = 0.03,
n = 2.0,
β = 0.2
)
u0721 = ComponentArray(
mA = 0.2,
mB = 0.3,
mC = 0.4,
A = 0.1,
B = 0.1,
C = 0.5
)
tspan = (0.0, 800.0)
prob721 = ODEProblem(model721!, u0721, tspan, ps721)ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(mA = 1, mB = 2, mC = 3, A = 4, B = 5, C = 6)}}} and tType Float64. In-place: true Non-trivial mass matrix: false timespan: (0.0, 800.0) u0: ComponentVector{Float64}(mA = 0.2, mB = 0.3, mC = 0.4, A = 0.1, B = 0.1, C = 0.5)
@time sol721 = solve(prob721, Tsit5()) 2.126951 seconds (8.07 M allocations: 407.473 MiB, 4.07% gc time, 99.97% compilation time)retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 691-element Vector{Float64}:
0.0
0.0014286712480576914
0.013295817654812879
0.04195540364909349
0.08458395388103226
0.13543750927592932
0.19582006887756317
0.2663933597892093
0.359749166563972
0.4892891916579355
⋮
790.9128717247945
792.0354268144121
793.1569796107343
794.2857471759745
795.431063966848
796.5999832553409
797.7925907252203
799.0048132399356
800.0
u: 691-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(mA = 1, mB = 2, mC = 3, A = 4, B = 5, C = 6)}}}}:
ComponentVector{Float64}(mA = 0.2, mB = 0.3, mC = 0.4, A = 0.1, B = 0.1, C = 0.5)
ComponentVector{Float64}(mA = 0.5403361928109343, mB = 0.7211224653006714, mC = 0.8209781853742835, A = 0.10007719934683137, B = 0.10011731198958067, C = 0.500031583424176)
ComponentVector{Float64}(mA = 3.3445686917162947, mB = 4.1948080080775565, mC = 4.293116571215766, A = 0.10445484065559739, B = 0.10571724539678706, C = 0.504918530231086)
ComponentVector{Float64}(mA = 9.862256612061595, mB = 12.38135118791294, mC = 12.465773188136598, A = 0.14182535843760377, B = 0.15265369477849908, C = 0.5501063999691335)
ComponentVector{Float64}(mA = 18.46032251481328, mB = 23.83685527865791, mC = 23.790059737848843, A = 0.2620278313349907, B = 0.30590549726625177, C = 0.7003009019509009)
ComponentVector{Float64}(mA = 26.249532197071474, mB = 35.63928962662804, mC = 34.905403323526, A = 0.4881499426134801, B = 0.605988604387404, C = 0.9931199784494682)
ComponentVector{Float64}(mA = 31.81366828339247, mB = 45.765184008478684, mC = 43.16437162981025, A = 0.83449036377949, B = 1.092000899729648, C = 1.455382353311618)
ComponentVector{Float64}(mA = 34.66815652739321, mB = 52.27310133304985, mC = 47.053230533448556, A = 1.2921878203930948, B = 1.7696593598504635, C = 2.0728299979836433)
ComponentVector{Float64}(mA = 35.32022666304059, mB = 55.140199309435445, mC = 47.35314269271503, A = 1.9192419429266043, B = 2.7377244558260805, C = 2.9129335517793122)
ComponentVector{Float64}(mA = 33.846648071977604, mB = 54.10975335029325, mC = 44.542357158993184, A = 2.7579425880653567, B = 4.072268694555362, C = 4.017500056850372)
⋮
ComponentVector{Float64}(mA = 0.2375946875195583, mB = 88.69246233369584, mC = 0.7055090274833062, A = 1.3082643642795184, B = 35.70871438896137, C = 32.17119264136293)
ComponentVector{Float64}(mA = 0.35139632090570183, mB = 112.98216106978667, mC = 0.35969614747647394, A = 1.103966719394066, B = 48.893475105011085, C = 25.803140994269167)
ComponentVector{Float64}(mA = 0.5294250571968119, mB = 135.5301952969134, mC = 0.19867065749213886, A = 0.9699604346173591, B = 64.18296493752092, C = 20.671893465522412)
ComponentVector{Float64}(mA = 0.8098393818329088, mB = 152.3633801512429, mC = 0.1220263131208807, A = 0.9081968161851209, B = 80.50136490615523, C = 16.525568401075567)
ComponentVector{Float64}(mA = 1.2565096026429454, mB = 159.22239579796147, mC = 0.0845987784004706, A = 0.9320384006188471, B = 96.15327227922734, C = 13.162966182583922)
ComponentVector{Float64}(mA = 1.9763681759496536, mB = 151.90878797780732, mC = 0.06601907654745044, A = 1.0718171361988387, B = 108.7870102575863, C = 10.434311027708265)
ComponentVector{Float64}(mA = 3.143175017645273, mB = 128.2536906731644, mC = 0.05708287805804966, A = 1.382766613618621, B = 115.60138248175028, C = 8.232960771671998)
ComponentVector{Float64}(mA = 5.033624964463263, mB = 92.7285231586031, mC = 0.05373464663806058, A = 1.9574341877403647, B = 114.46048668430842, C = 6.472296823011145)
ComponentVector{Float64}(mA = 7.390417846358349, mB = 63.115138390929125, mC = 0.05406535958530632, A = 2.718948201723007, B = 107.72487054745773, C = 5.313862289600622)
plot(t -> sol721(t).A, 0, tspan[2], labels="A")
plot!(t -> sol721(t).B, 0, tspan[2], labels="B")
plot!(t -> sol721(t).C, 0, tspan[2], xlabel="Time", ylabel="Concentration", title="Fig 7.21", labels="C")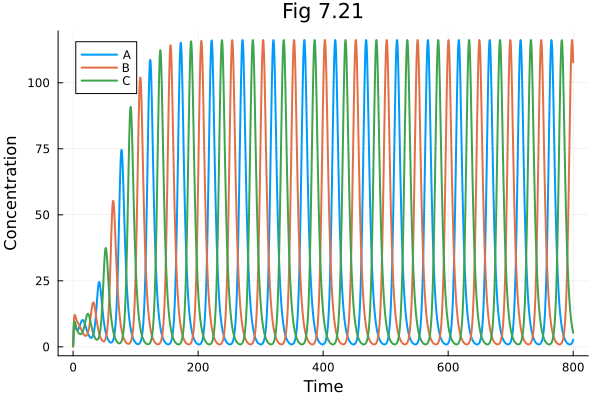
This notebook was generated using Literate.jl.
Back to top