using OrdinaryDiffEq
using ComponentArrays
using SimpleUnPack
using Plots
using Peaks
Plots.default(linewidth=2)Fig 7.19
Circadian rhythm model
hil(x, k=one(x)) = x / (x + k)
hil(x, k, n) = hil(x^n, k^n)
function model719!(D, u, p, t)
@unpack vs, vm, vd, ks, kt1, kt2, v1, v2, v3, v4, k1, k2, k3, k4, ki, km1, kd, n = p
@unpack M, P0, P1, P2, PN = u
rM = vs * hil(ki, PN, n) - vm * hil(M, km1)
rP01 = v1 * hil(P0, k1) - v2 * hil(P1, k2)
rP12 = v3 * hil(P1, k3) - v4 * hil(P2, k4)
rP2N = k1 * P2 - k2 * PN
rP2 = vd * hil(P2, kd)
D.M = rM
D.P0 = ks * M - rP01
D.P1 = rP01 - rP12
D.P2 = rP12 - rP2N - rP2
D.PN = rP2N
nothing
endmodel719! (generic function with 1 method)ps719 = ComponentArray(
vs = 0.76,
vm = 0.65,
vd = 0.95,
ks = 0.38,
kt1 = 1.9,
kt2 = 1.3,
v1 = 3.2,
v2 = 1.58,
v3 = 5.0,
v4 = 2.5,
k1 = 1.0,
k2 = 1.0,
k3 = 2.0,
k4 = 2.0,
ki = 1.0,
km1 = 0.5,
kd = 0.2,
n = 4
)
ics719 = ComponentArray(
M = 1.0,
P0 = 1.0,
P1 = 0.0,
P2 = 0.0,
PN = 0.0
)
tspan = (-50.0, 200.0)
prob719 = ODEProblem(model719!, ics719, tspan, ps719)ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(M = 1, P0 = 2, P1 = 3, P2 = 4, PN = 5)}}} and tType Float64. In-place: true Non-trivial mass matrix: false timespan: (-50.0, 200.0) u0: ComponentVector{Float64}(M = 1.0, P0 = 1.0, P1 = 0.0, P2 = 0.0, PN = 0.0)
@time sol719 = solve(prob719, TRBDF2()) 6.687719 seconds (23.11 M allocations: 1.129 GiB, 1.93% gc time, 99.93% compilation time)retcode: Success
Interpolation: 3rd order Hermite
t: 179-element Vector{Float64}:
-50.0
-49.99994872041174
-49.99943592452912
-49.99430796570293
-49.979217275906514
-49.9641265861101
-49.9266752405441
-49.8892238949781
-49.80587287439217
-49.71634933364356
⋮
186.61196838027118
187.99298449383178
189.4035707231591
191.14565689987697
193.0672918259186
194.98892675196024
196.58747195932074
198.36081121971054
200.0
u: 179-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(M = 1, P0 = 2, P1 = 3, P2 = 4, PN = 5)}}}}:
ComponentVector{Float64}(M = 1.0, P0 = 1.0, P1 = 0.0, P2 = 0.0, PN = 0.0)
ComponentVector{Float64}(M = 1.0000167512701272, P0 = 0.9999374436719781, P1 = 8.20374764209904e-5, P2 = 5.2577080303048654e-9, PN = 1.116818389016476e-13)
ComponentVector{Float64}(M = 1.0001842571480724, P0 = 0.9993124043621213, P1 = 0.0009013287672073863, P2 = 6.344858642472897e-7, PN = 1.4112359033690453e-10)
ComponentVector{Float64}(M = 1.0018586344769012, P0 = 0.9931137234766957, P1 = 0.008987532871512374, P2 = 6.291655050669721e-5, PN = 1.4073582405484636e-7)
ComponentVector{Float64}(M = 1.0067788776959867, P0 = 0.9753953029018657, P1 = 0.031711656257470314, P2 = 0.0007826761478524888, PN = 5.996096594710823e-6)
ComponentVector{Float64}(M = 1.0116885035560614, P0 = 0.9584125910062712, P1 = 0.052944661850366566, P2 = 0.002194038900703473, PN = 2.7820520658455485e-5)
ComponentVector{Float64}(M = 1.0238277385204875, P0 = 0.9190815202360649, P1 = 0.10007758939816325, P2 = 0.007848024956457134, PN = 0.0002077025390763281)
ComponentVector{Float64}(M = 1.035903503955488, P0 = 0.8832914414882437, P1 = 0.1404344835743439, P2 = 0.015566405635582368, PN = 0.0006286375297215101)
ComponentVector{Float64}(M = 1.0625583251849025, P0 = 0.8139056008465455, P1 = 0.21185450515841697, P2 = 0.035863218103131055, PN = 0.0026333647165893027)
ComponentVector{Float64}(M = 1.090859815075588, P0 = 0.7521755187808334, P1 = 0.2673943472124043, P2 = 0.05867821903560632, PN = 0.006467163279772056)
⋮
ComponentVector{Float64}(M = 1.6214299262723468, P0 = 0.4402282540508602, P1 = 0.3810790398490641, P2 = 0.26779579046399654, PN = 0.3067147342752848)
ComponentVector{Float64}(M = 1.962075259693916, P0 = 0.5547579824726457, P1 = 0.44667420537627156, P2 = 0.28936116695946723, PN = 0.28437513071180215)
ComponentVector{Float64}(M = 2.284044611019429, P0 = 0.6954049979190057, P1 = 0.5374177022388573, P2 = 0.34736212566893504, PN = 0.31286454409541037)
ComponentVector{Float64}(M = 2.6458021270474696, P0 = 0.8992226868261395, P1 = 0.6733712803692433, P2 = 0.45664587553419567, PN = 0.3961275700377714)
ComponentVector{Float64}(M = 2.976633121529561, P0 = 1.1558447299800882, P1 = 0.8464698366079212, P2 = 0.6186143797215962, PN = 0.5349586986603169)
ComponentVector{Float64}(M = 3.1626524274745935, P0 = 1.4168031221000454, P1 = 1.0318932888723666, P2 = 0.8169194234540103, PN = 0.7143451954249381)
ComponentVector{Float64}(M = 3.1250654195596623, P0 = 1.5860863513103727, P1 = 1.1792135076466939, P2 = 0.9997697911533785, PN = 0.8869756918802206)
ComponentVector{Float64}(M = 2.8319709164579767, P0 = 1.643468292948715, P1 = 1.3073148778016368, P2 = 1.202205618304551, PN = 1.0887116977435431)
ComponentVector{Float64}(M = 2.3694220419868715, P0 = 1.527589868983711, P1 = 1.3628261445323515, P2 = 1.363490055897846, PN = 1.2642760549080352)
_total_P(sol) = sol.P0 .+ sol.P1 .+ sol.P2 .+ sol.PN
plot(t->sol719(t).M, 0, tspan[2], xlabel="Time", ylabel=" Concentration", title="Fig 7.19 A", label="M")
plot!(t->sol719(t).PN, 0, tspan[2], label="Nuclear PER")
plot!(t->_total_P(sol719(t)), 0, tspan[2], label="Total PER")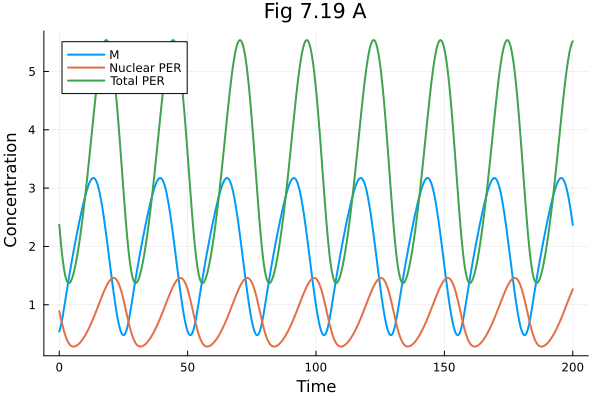
This notebook was generated using Literate.jl.
Back to top