using ModelingToolkit
using OrdinaryDiffEq, SteadyStateDiffEq, DiffEqCallbacks
using Plots
using CSV
using DataFrames
using CurveFit
using CaMKIIModel
using CaMKIIModel: second
Plots.default(lw=1.5)Pacing durations
Experiments vs simulations.
Experiments
30 seconds resting + N seconds 1Hz pacing + resting.
durationdf = CSV.read(joinpath(@__DIR__, "data/CaMKAR-duration.csv"), DataFrame)
ts = durationdf[!, "Time(sec)"]
fifteen = durationdf[!, "1Hz 15sec (Mean)"]
fifteen_error = durationdf[!, "1Hz 15sec (SD)"] ./ sqrt.(durationdf[!, "1Hz 15sec (N)"])
thirty = durationdf[!, "1Hz 30sec (Mean)"] .+ 0.25
thirty_error = durationdf[!, "1Hz 30sec (SD)"] ./ sqrt.(durationdf[!, "1Hz 30sec (N)"])
sixty = durationdf[!, "1Hz 60sec (Mean)"]
sixty_error = durationdf[!, "1Hz 60sec (SD)"] ./ sqrt.(durationdf[!, "1Hz 60sec (N)"])
ninety = durationdf[!, "1Hz 90sec (Mean)"] .- 0.25
ninety_error = durationdf[!, "1Hz 90sec (SD)"] ./ sqrt.(durationdf[!, "1Hz 90sec (N)"])
# 30 sec timeseries +0.25 and 90 sec timeseries -0.25 for a consistent baseline before pacing.
plot(ts, fifteen, yerr=fifteen_error, lab="15 sec", color=:blue, markerstrokecolor=:blue)
plot!(ts, thirty, yerr=thirty_error, lab="30 sec", color=:red, markerstrokecolor=:red)
plot!(ts, sixty, yerr=sixty_error, lab="60 sec", color=:orange, markerstrokecolor=:orange)
plot!(ts, ninety, yerr=ninety_error, lab="90 sec", color=:green, markerstrokecolor=:green)
plot!(title="Experiment", xlabel="Time (s)", ylabel="CaMKII activity (AU)")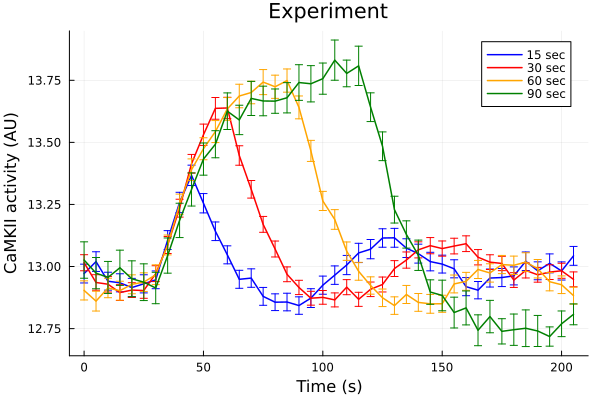
savefig("pacing-duration-exp.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pacing-duration-exp.pdf"Simulation
@time "Build system" sys = build_neonatal_ecc_sys(simplify=true, reduce_iso=true, reduce_camk=true)
tend = 500second
@time "Build problem" prob = ODEProblem(sys, [sys.kdeph_CaMK => inv(10second)], tend)
@time "Remake problem" prob_n0a2 = remake(prob, p=[sys.k_P1_P2=>0, sys.kdeph_CaMK => inv(12second)])
stimstart = 100second
stimend = 300second
@unpack Istim = sys
alg = KenCarp47()Build system: 56.326003 seconds (96.00 M allocations: 4.527 GiB, 2.56% gc time, 94.79% compilation time: 32% of which was recompilation)
Build problem: 29.505914 seconds (54.30 M allocations: 2.609 GiB, 2.10% gc time, 96.83% compilation time: 42% of which was recompilation)
Remake problem: 5.272468 seconds (9.24 M allocations: 413.525 MiB, 1.68% gc time, 85.33% compilation time: <1% of which was recompilation)KenCarp47(; linsolve = nothing, nlsolve = OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}(1//100, 10, 1//5, 1//5, false, true, nothing), precs = DEFAULT_PRECS, smooth_est = true, extrapolant = linear, controller = PI, autodiff = ADTypes.AutoForwardDiff(),)stimstart = 30second
callback15 = build_stim_callbacks(Istim, stimstart + 15second; period=1second, starttime=stimstart)
sol15 = solve(prob, alg; callback=callback15)
sol15_n0a2 = solve(prob_n0a2, alg; callback=callback15)
callback30 = build_stim_callbacks(Istim, stimstart + 30second; period=1second, starttime=stimstart)
sol30 = solve(prob, alg; callback=callback30)
sol30_n0a2 = solve(prob_n0a2, alg; callback=callback30)
callback60 = build_stim_callbacks(Istim, stimstart + 60second; period=1second, starttime=stimstart)
sol60 = solve(prob, alg; callback=callback60)
sol60_n0a2 = solve(prob_n0a2, alg; callback=callback60)
callback90 = build_stim_callbacks(Istim, stimstart + 90second; period=1second, starttime=stimstart)
sol90 = solve(prob, alg; callback=callback90)
sol90_n0a2 = solve(prob_n0a2, alg; callback=callback90)
idxs = (sys.t / 1000, sys.CaMKAct * 100)((1//1000)*t, 100CaMKAct(t))plot(sol15, idxs=idxs, tspan=(0second, 205second), lab="15 sec", color=:blue)
plot!(sol30, idxs=idxs, tspan=(0second, 205second), lab="30 sec", color=:red)
plot!(sol60, idxs=idxs, tspan=(0second, 205second), lab="60 sec", color=:orange)
plot!(sol90, idxs=idxs, tspan=(0second, 205second), lab="90 sec", color=:green)
plot!(title="Simulation", xlabel="Time (s)", ylabel="CaMKII activity (%)")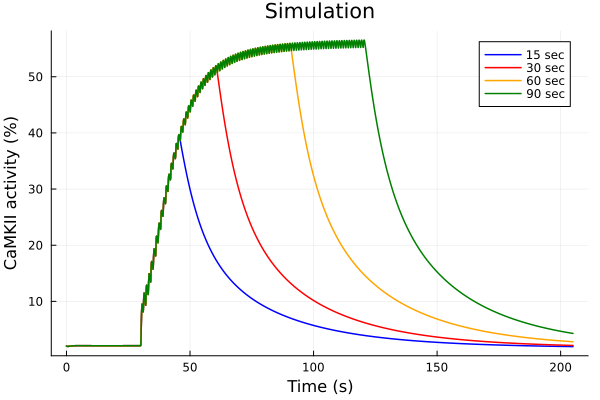
savefig("pacing-duration-sim.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pacing-duration-sim.pdf"Decay rates
Fit against an exponential decay model.
decay_model(p, x) = @. p[1] * exp(-x / p[2]) + p[3]decay_model (generic function with 1 method)Data from experiments Record 50 seconds after pacing ends
ts = collect(range(0.0, stop=50.0, step=5.0))
ydata_15 = fifteen[10:20]
ydata_30 = thirty[13:23]
ydata_60 = sixty[19:29]
ydata_90 = ninety[25:35]11-element Vector{Float64}:
13.64164293
13.48430494
13.22906779
13.12909541
13.04527631
12.89725458
12.88348484
12.81471802
12.83336721
12.74340616
12.79848118Simulation points
ysim_15 = sol15(stimstart+15second:5second:stimstart+15second+50second ; idxs=sys.CaMKAct * 100).u
ysim_30 = sol30(stimstart+30second:5second:stimstart+30second+50second ; idxs=sys.CaMKAct * 100).u
ysim_60 = sol60(stimstart+60second:5second:stimstart+60second+50second ; idxs=sys.CaMKAct * 100).u
ysim_90 = sol90(stimstart+90second:5second:stimstart+90second+50second ; idxs=sys.CaMKAct * 100).u
ysim_15_noa2 = sol15_n0a2(stimstart+15second:5second:stimstart+15second+50second ; idxs=sys.CaMKAct * 100).u
ysim_30_noa2 = sol30_n0a2(stimstart+30second:5second:stimstart+30second+50second ; idxs=sys.CaMKAct * 100).u
ysim_60_noa2 = sol60_n0a2(stimstart+60second:5second:stimstart+60second+50second ; idxs=sys.CaMKAct * 100).u
ysim_90_noa2 = sol90_n0a2(stimstart+90second:5second:stimstart+90second+50second ; idxs=sys.CaMKAct * 100).u11-element Vector{Float64}:
55.03256009581696
42.748889487130484
31.5469143687927
23.958566393932955
18.681601264020344
14.893975412828087
12.09871620525982
9.989285264633097
8.369125188595273
7.107408304997032
6.113833844174743Fit data to an exponential decay model
fit_15 = solve(CurveFitProblem(ts, ydata_15), ExpSumFitAlgorithm(n=1, withconst=true))
fit_30 = solve(CurveFitProblem(ts, ydata_30), ExpSumFitAlgorithm(n=1, withconst=true))
fit_60 = solve(CurveFitProblem(ts, ydata_60), ExpSumFitAlgorithm(n=1, withconst=true))
fit_90 = solve(CurveFitProblem(ts, ydata_90), ExpSumFitAlgorithm(n=1, withconst=true))retcode: Success
alg: ExpSumFitAlgorithm
residuals mean: 9.689219124001365e-16
u: [12.698712831736712, 0.9676132832582899, -0.05530003616111157]Fit simulation results to an exponential decay model
fit_sim_15 = solve(CurveFitProblem(ts, ysim_15), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_30 = solve(CurveFitProblem(ts, ysim_30), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_60 = solve(CurveFitProblem(ts, ysim_60), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_90 = solve(CurveFitProblem(ts, ysim_90), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_15_noa2 = solve(CurveFitProblem(ts, ysim_15_noa2), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_30_noa2 = solve(CurveFitProblem(ts, ysim_30_noa2), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_60_noa2 = solve(CurveFitProblem(ts, ysim_60_noa2), ExpSumFitAlgorithm(n=1, withconst=true))
fit_sim_90_noa2 = solve(CurveFitProblem(ts, ysim_90_noa2), ExpSumFitAlgorithm(n=1, withconst=true))retcode: Success
alg: ExpSumFitAlgorithm
residuals mean: -1.2918958832001822e-15
u: [3.7601679933892163, 51.64149625780551, -0.06118048802471266]Fitting results (experiments)
p1 = plot(ts, ydata_15, label="Exp 15 sec")
plot!(p1, ts, predict(fit_15), label="Fit", linestyle=:dash)
p2 = plot(ts, ydata_30, label="Exp 30 sec")
plot!(p2, ts, predict(fit_30), label="Fit", linestyle=:dash)
p3 = plot(ts, ydata_60, label="Exp 60 sec")
plot!(p3, ts, predict(fit_60), label="Fit", linestyle=:dash)
p4 = plot(ts, ydata_90, label="Exp 90 sec")
plot!(p4, ts, predict(fit_90), label="Fit", linestyle=:dash)
plot(p1, p2, p3, p4, layout=(2,2), title="Experiment Fits", xlabel="Time (s)", ylabel="CaMKII activity (AU)")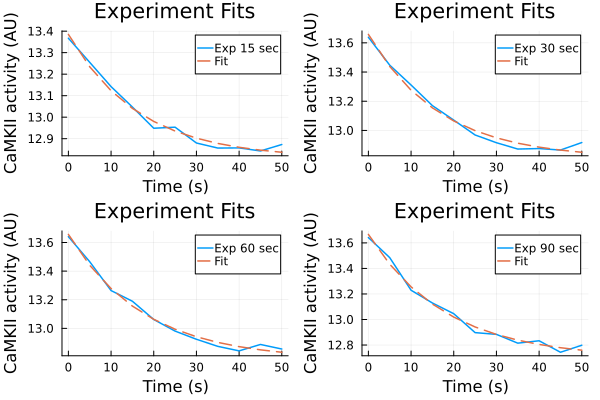
Fitting results (simulations)
p1s = plot(ts, ysim_15, label="Sim 15 sec")
plot!(p1s, ts, predict(fit_sim_15), label="Fit", linestyle=:dash)
p2s = plot(ts, ysim_30, label="Sim 30 sec")
plot!(p2s, ts, predict(fit_sim_30), label="Fit", linestyle=:dash)
p3s = plot(ts, ysim_60, label="Sim 60 sec")
plot!(p3s, ts, predict(fit_sim_60), label="Fit", linestyle=:dash)
p4s = plot(ts, ysim_90, label="Sim 90 sec")
plot!(p4s, ts, predict(fit_sim_90), label="Fit", linestyle=:dash)
plot(p1s, p2s, p3s, p4s, layout=(2,2), title="Simulation Fits", xlabel="Time (s)", ylabel="CaMKII activity (%)")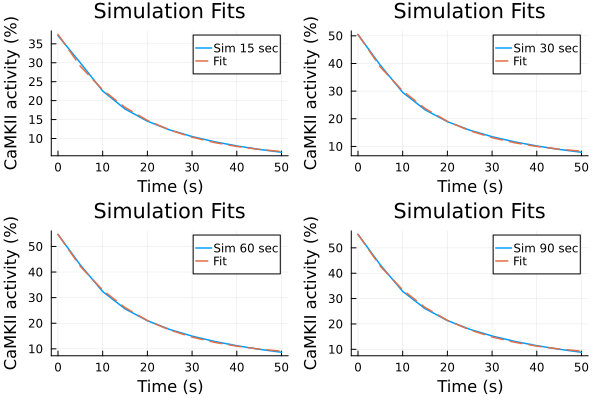
Calculate time scales (tau) from fit parameters
tau_exp_15 = inv(-fit_15.u.λ[])
tau_exp_30 = inv(-fit_30.u.λ[])
tau_exp_60 = inv(-fit_60.u.λ[])
tau_exp_90 = inv(-fit_90.u.λ[])
tau_sim_15 = inv(-fit_sim_15.u.λ[])
tau_sim_30 = inv(-fit_sim_30.u.λ[])
tau_sim_60 = inv(-fit_sim_60.u.λ[])
tau_sim_90 = inv(-fit_sim_90.u.λ[])
tau_sim_15_noa2 = inv(-fit_sim_15_noa2.u.λ[])
tau_sim_30_noa2 = inv(-fit_sim_30_noa2.u.λ[])
tau_sim_60_noa2 = inv(-fit_sim_60_noa2.u.λ[])
tau_sim_90_noa2 = inv(-fit_sim_90_noa2.u.λ[])16.345080470689766println("The time scales for experiments: ")
for (tau, dur) in zip((tau_exp_15, tau_exp_30, tau_exp_60, tau_exp_90), (15, 30, 60, 90))
println("$dur sec pacing is $(round(tau; digits=2)) seconds.")
end
println("The time scales for simulations: ")
for (tau, dur) in zip((tau_sim_15, tau_sim_30, tau_sim_60, tau_sim_90), (15, 30, 60, 90))
println("$dur sec pacing is $(round(tau; digits=2)) seconds.")
end
println("The time scale for simulation without CaMKII A2: ")
for (tau, dur) in zip((tau_sim_15_noa2, tau_sim_30_noa2, tau_sim_60_noa2, tau_sim_90_noa2), (15, 30, 60, 90))
println("$dur sec pacing is $(round(tau; digits=2)) seconds.")
endThe time scales for experiments:
15 sec pacing is 16.48 seconds.
30 sec pacing is 16.73 seconds.
60 sec pacing is 17.65 seconds.
90 sec pacing is 18.08 seconds.
The time scales for simulations:
15 sec pacing is 16.76 seconds.
30 sec pacing is 16.13 seconds.
60 sec pacing is 16.54 seconds.
90 sec pacing is 16.63 seconds.
The time scale for simulation without CaMKII A2:
15 sec pacing is 18.75 seconds.
30 sec pacing is 16.62 seconds.
60 sec pacing is 16.34 seconds.
90 sec pacing is 16.35 seconds.Plot pacing time vs decay time scale
pacing_durations = [15.0, 30.0, 60.0, 90.0]
tau_experiments = [tau_exp_15, tau_exp_30, tau_exp_60, tau_exp_90]
tau_simulations = [tau_sim_15, tau_sim_30, tau_sim_60, tau_sim_90]
tau_simulations_noa2 = [tau_sim_15_noa2, tau_sim_30_noa2, tau_sim_60_noa2, tau_sim_90_noa2]
plot(pacing_durations, tau_experiments, label="Experiments", marker=:circle, color=:blue)
plot!(pacing_durations, tau_simulations, label="Simulations", marker=:square, color=:red)
plot!(pacing_durations, tau_simulations_noa2, label="Simulations no A2", marker=:diamond, color=:green)
plot!(title="Pacing Duration vs Decay Time Scale", xlabel="Pacing Duration (s)", ylabel="Decay Time Scale (s)")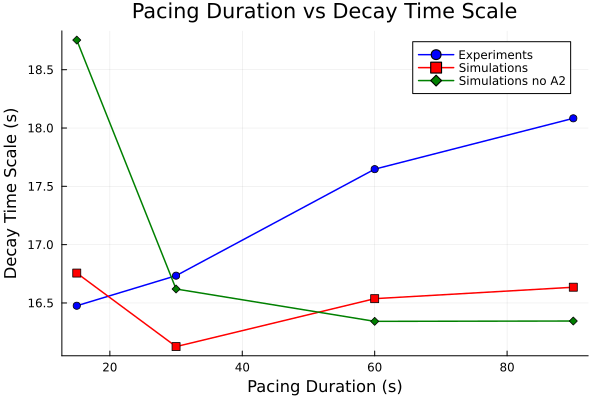
savefig("pacing-decay-exp-sim.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pacing-decay-exp-sim.pdf"Phosphorylated fraction
idxs = (sys.t / 1000, (sys.CaMKP + sys.CaMKA + sys.CaMKA2) * 100)
plot(sol15, idxs=idxs, tspan=(0second, 205second), lab="15 sec", color=:blue)
plot!(sol30, idxs=idxs, tspan=(0second, 205second), lab="30 sec", color=:red)
plot!(sol60, idxs=idxs, tspan=(0second, 205second), lab="60 sec", color=:orange)
plot!(sol90, idxs=idxs, tspan=(0second, 205second), lab="90 sec", color=:green)
plot!(title="Simulation", xlabel="Time (s)", ylabel="Phosphorylated CaMKII (%)")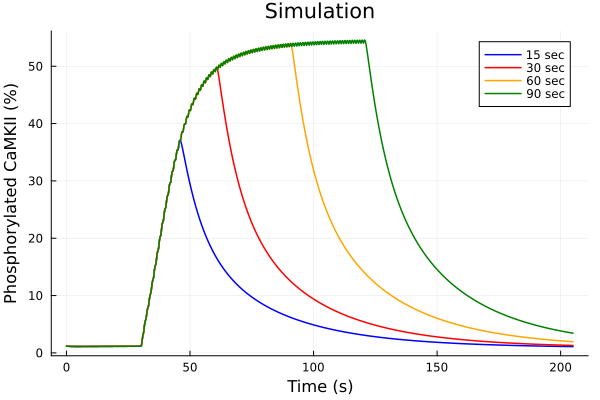
savefig("pacing-duration-phos.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pacing-duration-phos.pdf"This notebook was generated using Literate.jl.