using ModelingToolkit
using OrdinaryDiffEq, SteadyStateDiffEq, DiffEqCallbacks
using Plots
using CurveFit
using CaMKIIModel
using CaMKIIModel: μM, hil, Hz, hilr, second
Plots.default(lw=1.5)b1AR system simplification
Fitting sensitivity to ISO.
Setup b1AR system
@parameters ATP = 5000μM ISO = 0μM
@time "Build system" sys = get_bar_sys(ATP, ISO; simplify=true)
@time "Build problem" prob = SteadyStateProblem(sys, [])Build system: 2.081301 seconds (3.56 M allocations: 173.805 MiB, 2.05% gc time, 98.26% compilation time: 2% of which was recompilation)
Build problem: 0.622695 seconds (3.00 M allocations: 150.445 MiB, 93.90% compilation time: 8% of which was recompilation)SteadyStateProblem with uType Vector{Float64}. In-place: true u0: 27-element Vector{Float64}: 0.0 0.01794 0.01313 0.01204 60.75646 41.19479 98.33936 0.19135 0.00033 0.02753 ⋮ 0.00589 0.00814 0.0011 0.00047 0.00066 0.05214 7.0e-5 0.00294 6.0e-5
Log scale for ISO concentration
alg = DynamicSS(KenCarp47())
iso = logrange(1e-4μM, 1μM, length=1001)
prob_func = (prob, i, repeat) -> (prob.ps[ISO] = iso[i]; prob)
sol = solve(prob, alg; abstol=1e-10, reltol=1e-10) ## warmup
@time "Solve problem" sim = solve(EnsembleProblem(prob; prob_func), alg; trajectories=length(iso), abstol=1e-10, reltol=1e-10);Solve problem: 11.003574 seconds (61.73 M allocations: 3.723 GiB, 18.15% gc time, 2.22% compilation time)Convienience functions
"""Extract values from ensemble simulations by a symbol"""
extract(sim, k) = map(s -> s[k], sim)Main.var"##355".extractxopts = (xlims=(iso[begin], iso[end]), minorgrid=true, xscale=:log10, xlabel="ISO (μM)",)
plot(iso, extract(sim, sys.cAMP); lab="cAMP", ylabel="Conc. (μM)", legend=:topleft, xopts...)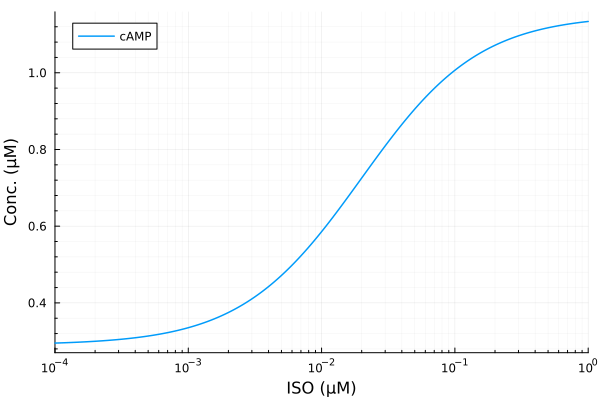
plot(iso, extract(sim, sys.PKACI / sys.RItot); lab="PKACI", ylabel="Activation fraction")
plot!(iso, extract(sim, sys.PKACII / sys.RIItot), lab="PKACII")
plot!(iso, extract(sim, sys.PP1 / sys.PP1totBA), lab="PP1", legend=:topleft; xopts...)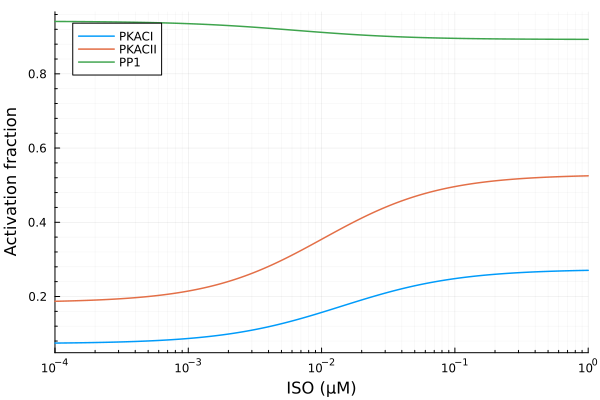
PKACI activity
model(p, x) = @. p[1] * hil(x, p[2]) + p[3]
xdata = iso
ydata = extract(sim, sys.PKACI / sys.RItot)
p0 = [0.3, 0.01μM, 0.08]
prob = NonlinearCurveFitProblem(model, p0, xdata, ydata)
@time "Fit PKACI" fit_pkac1 = solve(prob)Fit PKACI: 1.816292 seconds (7.86 M allocations: 394.796 MiB, 2.93% gc time, 99.84% compilation time)retcode: StalledSuccess
f: model
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 2.3845949080360507e-18
u: [0.1993756134588762, 0.013906465784162514, 0.07340261656613752]println("PKACI")
println("Basal activity: ", fit_pkac1.u[3])
println("Activated activity: ", fit_pkac1.u[1])
println("Michaelis constant: ", fit_pkac1.u[2], " μM")
println("RMSE: ", mse(fit_pkac1) |> sqrt)PKACI
Basal activity: 0.07340261656613752
Activated activity: 0.1993756134588762
Michaelis constant: 0.013906465784162514 μM
RMSE: 0.000327384332025576p1 = plot(xdata, [ydata predict(fit_pkac1)], lab=["Full model" "Fitted"], line=[:dash :dot], title="PKACI", legend=:topleft; xopts...)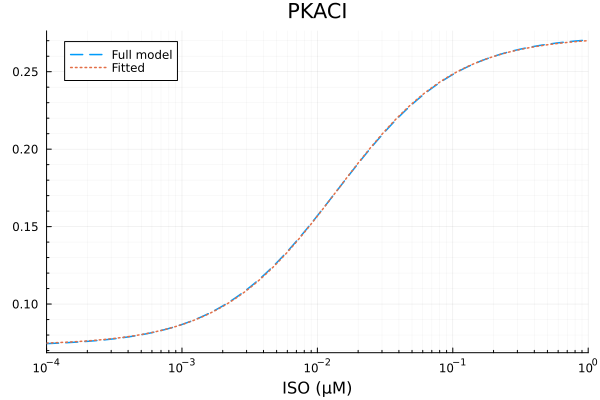
savefig("pkaci_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pkaci_fit.pdf"p2 = plot(xdata, residuals(fit_pkac1) ./ ydata .* 100; title="PKACI error (%)", lab=false, xopts...)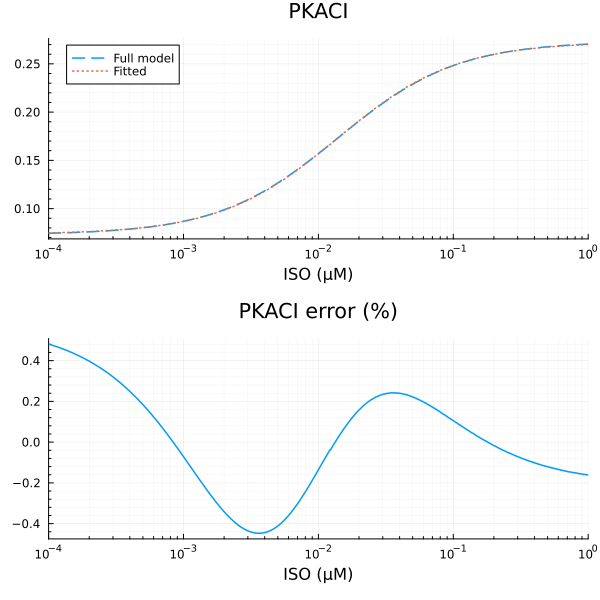
PKACII activity
xdata = iso
ydata = extract(sim, sys.PKACII / sys.RIItot)
p0 = [0.4, 0.01μM, 0.2]
prob = NonlinearCurveFitProblem(model, p0, xdata, ydata)
@time fit_pkac2 = solve(prob) 0.001596 seconds (1.61 k allocations: 5.104 MiB)retcode: StalledSuccess
f: model
alg: __FallbackNonlinearFitAlgorithm
residuals mean: -8.845183437947675e-18
u: [0.34437425141770245, 0.01025120242851867, 0.18399233394249956]println("PKACII")
println("Basal activity: ", fit_pkac2.u[3])
println("Activated activity: ", fit_pkac2.u[1])
println("Michaelis constant: ", fit_pkac2.u[2], " μM")
println("RMSE: ", mse(fit_pkac2) |> sqrt)PKACII
Basal activity: 0.18399233394249956
Activated activity: 0.34437425141770245
Michaelis constant: 0.01025120242851867 μM
RMSE: 0.00024403431636079204p1 = plot(xdata, [ydata predict(fit_pkac2)], lab=["Full model" "Fitted"], line=[:dash :dot], title="PKACII", legend=:topleft; xopts...)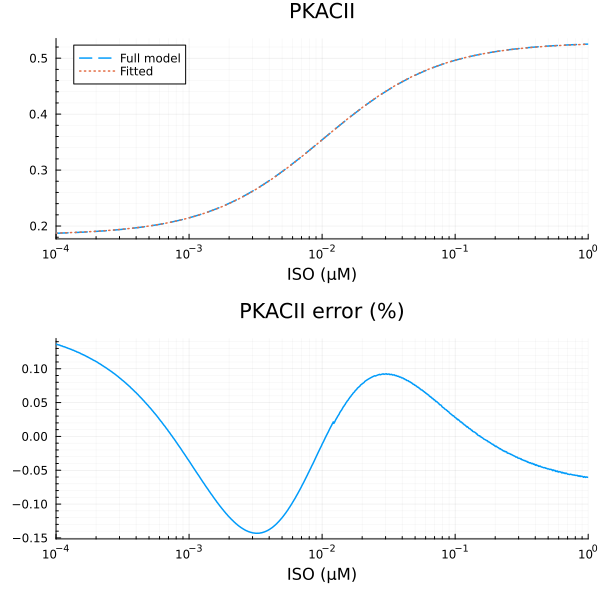
savefig("pkacii_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pkacii_fit.pdf"p2 = plot(xdata, residuals(fit_pkac2) ./ ydata .* 100; title="PKACII error (%)", lab=false, xopts...)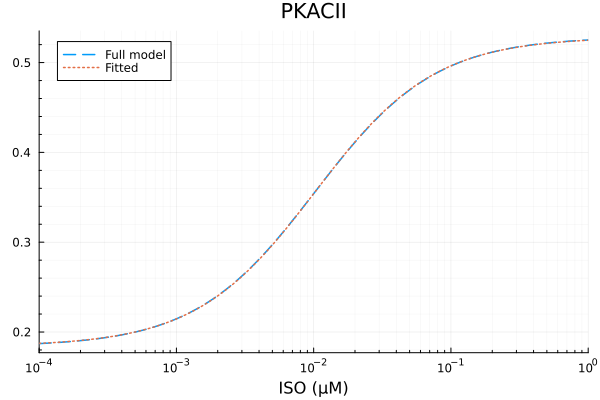
PP1 activity
model_pp1(p, x) = @. p[1] * hil(p[2], x) + p[3]
xdata = iso
ydata = extract(sim, sys.PP1 / sys.PP1totBA)
p0 = [0.1, 3e-3μM, 0.8]
prob = NonlinearCurveFitProblem(model_pp1, p0, xdata, ydata)
@time fit_pp1 = solve(prob) 1.769203 seconds (7.89 M allocations: 396.206 MiB, 3.11% gc time, 99.84% compilation time)retcode: StalledSuccess
f: model_pp1
alg: __FallbackNonlinearFitAlgorithm
residuals mean: -1.6636708660716632e-18
u: [0.049192292250778, 0.006361982106885943, 0.8927128301424797]println("PP1")
println("Repressible activity: ", fit_pp1.u[1])
println("Minimal activity: ", fit_pp1.u[3])
println("Repressive Michaelis constant: ", fit_pp1.u[2], " μM")
println("RMSE: ", mse(fit_pp1) |> sqrt)PP1
Repressible activity: 0.049192292250778
Minimal activity: 0.8927128301424797
Repressive Michaelis constant: 0.006361982106885943 μM
RMSE: 3.545892402560016e-5p1 = plot(xdata, [ydata predict(fit_pp1)], lab=["Full model" "Fitted"], line=[:dash :dot], title="PP1", legend=:topright; xopts...)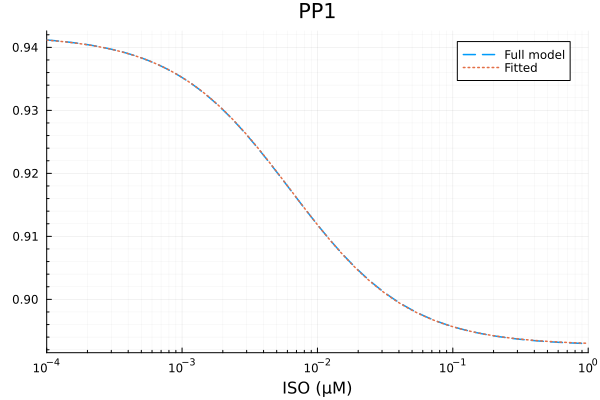
savefig("pp1_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/pp1_fit.pdf"p2 = plot(xdata, residuals(fit_pp1) ./ ydata .* 100; title="PP1 error (%)", lab=false, xopts...)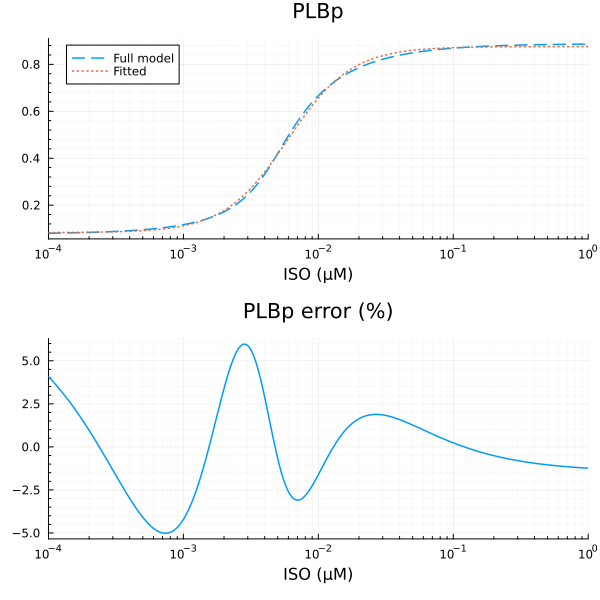
PLBp
xdata = iso
ydata = extract(sim, sys.PLBp / sys.PLBtotBA)
plot(xdata, ydata, title="PLBp fraction", lab=false; xopts...)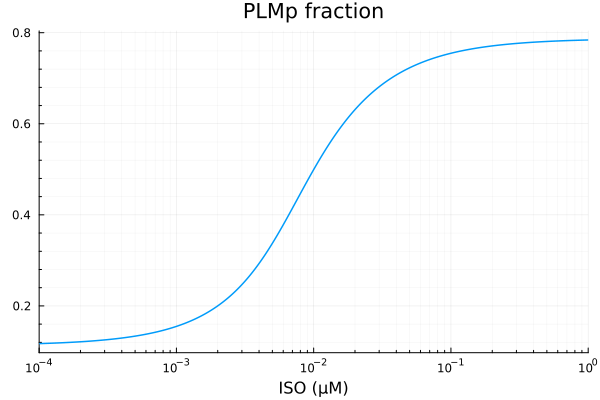
model_plb(p, x) = @. p[1] * hil(x, p[2], p[3]) + p[4]
p0 = [0.8, 1e-2μM, 1.0, 0.1]
prob = NonlinearCurveFitProblem(model_plb, p0, xdata, ydata)
@time fit_plb = solve(prob) 1.636421 seconds (7.61 M allocations: 386.009 MiB, 3.03% gc time, 99.24% compilation time)retcode: StalledSuccess
f: model_plb
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 1.238048402834996e-17
u: [0.7923227890350578, 0.0059366893498588105, 1.8386617510976648, 0.0830117928849273]println("PLBp")
println("Basal activity: ", fit_plb.u[4])
println("Activated activity: ", fit_plb.u[1])
println("Michaelis constant: ", fit_plb.u[2], " μM")
println("Hill coefficient: ", fit_plb.u[3])
println("RMSE: ", mse(fit_plb) |> sqrt)PLBp
Basal activity: 0.0830117928849273
Activated activity: 0.7923227890350578
Michaelis constant: 0.0059366893498588105 μM
Hill coefficient: 1.8386617510976648
RMSE: 0.008435704441782209p1 = plot(xdata, [ydata predict(fit_plb)], lab=["Full model" "Fitted"], line=[:dash :dot], title="PLBp", legend=:topleft; xopts...)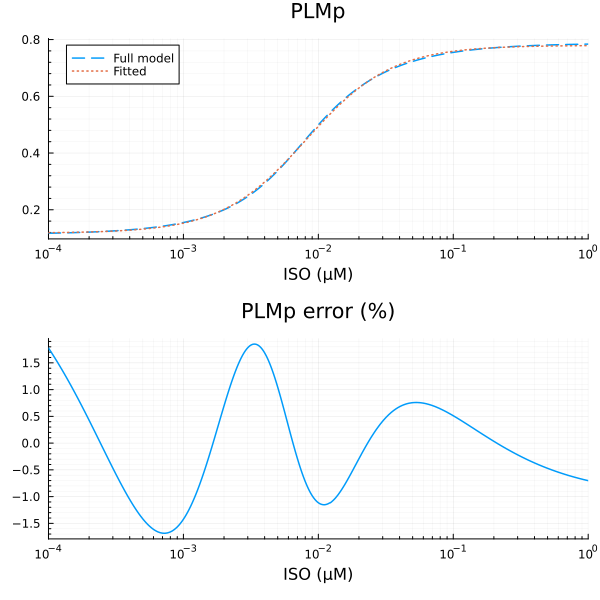
savefig("plbp_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/plbp_fit.pdf"p2 = plot(xdata, residuals(fit_plb) ./ ydata .* 100; title="PLBp error (%)", lab=false, xopts...)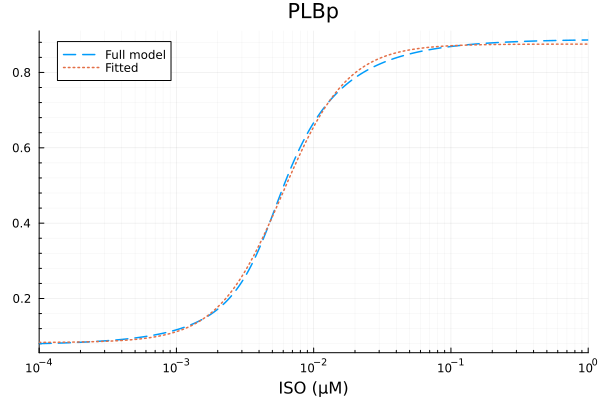
PLMp
xdata = iso
ydata = extract(sim, sys.PLMp / sys.PLMtotBA)
plot(xdata, ydata, title="PLMp fraction", lab=false; xopts...)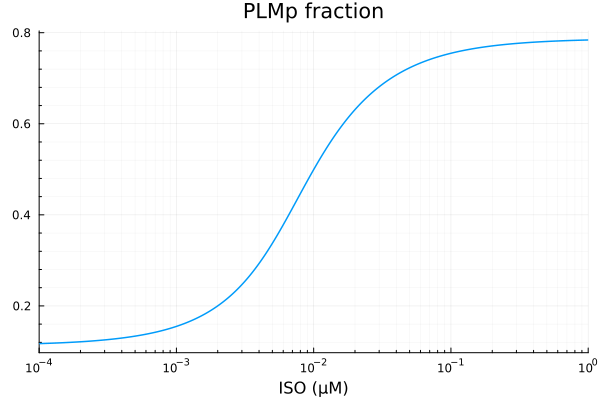
model_plm(p, x) = @. p[1] * hil(x, p[2], p[3]) + p[4]
p0 = [0.8, 1e-2μM, 1.0, 0.1]
prob = NonlinearCurveFitProblem(model_plm, p0, xdata, ydata)
@time fit_plm = solve(prob) 1.671122 seconds (7.61 M allocations: 384.969 MiB, 3.25% gc time, 99.35% compilation time)retcode: StalledSuccess
f: model_plm
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 1.263003465826071e-17
u: [0.6617221457892768, 0.008181792011738466, 1.3710370061445, 0.11772711157130936]println("PLMp")
println("Basal activity: ", fit_plm.u[4])
println("Activated activity: ", fit_plm.u[1])
println("Michaelis constant: ", fit_plm.u[2], " μM")
println("Hill coefficient: ", fit_plm.u[3])
println("RMSE: ", mse(fit_plm) |> sqrt)PLMp
Basal activity: 0.11772711157130936
Activated activity: 0.6617221457892768
Michaelis constant: 0.008181792011738466 μM
Hill coefficient: 1.3710370061445
RMSE: 0.003280102867227682p1 = plot(xdata, [ydata predict(fit_plm)], lab=["Full model" "Fitted"], line=[:dash :dot], title="PLMp", legend=:topleft; xopts...)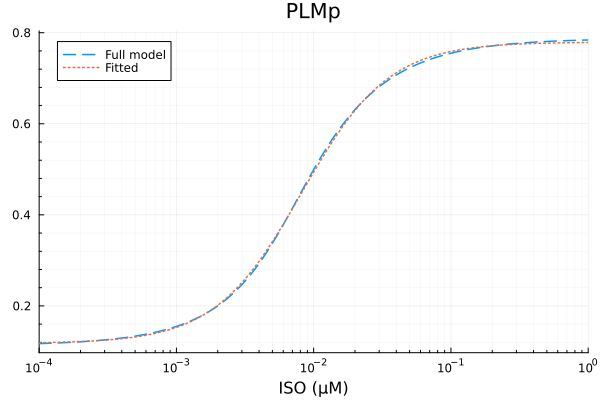
savefig("plmp_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/plmp_fit.pdf"p2 = plot(xdata, residuals(fit_plm) ./ ydata .* 100; title="PLMp error (%)", lab=false, xopts...)
# TnIp
xdata = iso
ydata = extract(sim, sys.TnIp / sys.TnItotBA)
plot(xdata, ydata, title="TnIp fraction", lab=false; xopts...)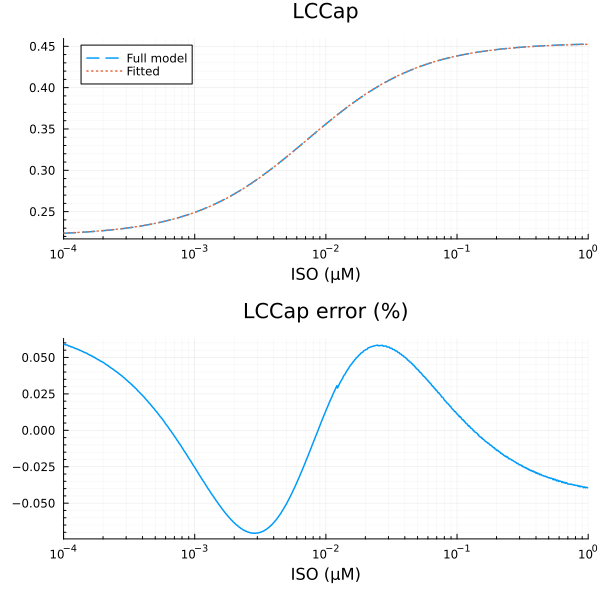
model_tni(p, x) = @. p[1] * hil(x, p[2], p[3]) + p[4]
p0 = [0.8, 1e-2μM, 1.0, 0.1]
lb = [0.1, 1e-9μM, 1.0, 0.0]
prob = NonlinearCurveFitProblem(model_tni, p0, xdata, ydata)
@time fit_tni = solve(prob) 1.583143 seconds (7.61 M allocations: 385.236 MiB, 99.27% compilation time)retcode: StalledSuccess
f: model_tni
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 1.3877787807814457e-17
u: [0.7481983451147566, 0.007856410455884566, 1.6973368341572719, 0.06752950505386603]println("TnIp")
println("Basal activity: ", fit_tni.u[4])
println("Activated activity: ", fit_tni.u[1])
println("Michaelis constant: ", fit_tni.u[2], " μM")
println("Hill coefficient: ", fit_tni.u[3])
println("RMSE: ", mse(fit_tni) |> sqrt)TnIp
Basal activity: 0.06752950505386603
Activated activity: 0.7481983451147566
Michaelis constant: 0.007856410455884566 μM
Hill coefficient: 1.6973368341572719
RMSE: 0.007451503066186062p1 = plot(xdata, [ydata predict(fit_tni)], lab=["Full model" "Fitted"], line=[:dash :dot], title="TnIp", legend=:topleft; xopts...)
savefig("tni_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/tni_fit.pdf"p2 = plot(xdata, residuals(fit_tni) ./ ydata .* 100; title="TnIp error (%)", lab=false, xopts...)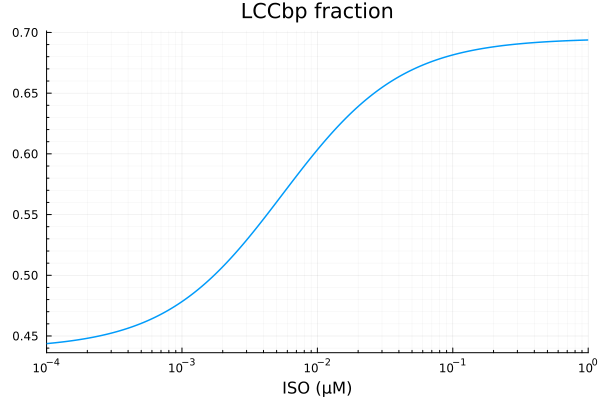
LCCap
xdata = iso
ydata = extract(sim, sys.LCCap / sys.LCCtotBA)
plot(xdata, ydata, title="LCCap fraction", lab=false; xopts...)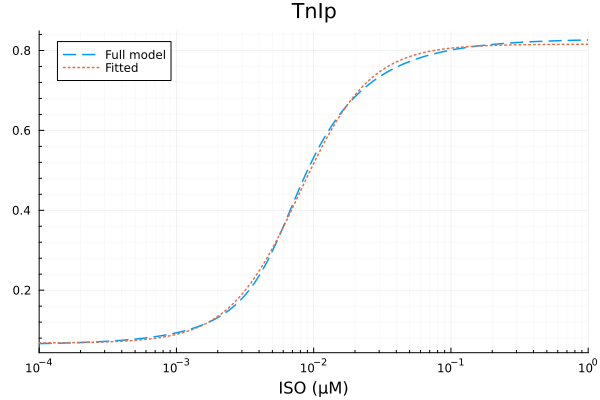
model_lcc(p, x) = @. p[1] * hil(x, p[2]) + p[3]
p0 = [0.8, 1e-2μM, 0.1]
prob = NonlinearCurveFitProblem(model_lcc, p0, xdata, ydata)
@time fit_lcca = solve(prob) 1.564709 seconds (7.53 M allocations: 379.726 MiB, 99.83% compilation time)retcode: StalledSuccess
f: model_lcc
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 5.2682910758936e-18
u: [0.2333838105668288, 0.00726345769052629, 0.22081925973557476]println("LCCap")
println("Basal activity: ", fit_lcca.u[3])
println("Activated activity: ", fit_lcca.u[1])
println("Michaelis constant: ", fit_lcca.u[2], " μM")
println("RMSE: ", mse(fit_lcca) |> sqrt)LCCap
Basal activity: 0.22081925973557476
Activated activity: 0.2333838105668288
Michaelis constant: 0.00726345769052629 μM
RMSE: 0.0001349333609235451p1 = plot(xdata, [ydata predict(fit_lcca)], lab=["Full model" "Fitted"], line=[:dash :dot], title="LCCap", legend=:topleft; xopts...)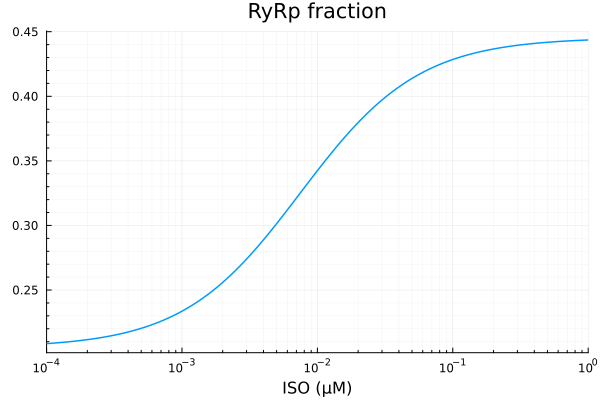
savefig("lcca_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/lcca_fit.pdf"plot(xdata, residuals(fit_lcca) ./ ydata .* 100; title="LCCap error (%)", lab=false, xopts...)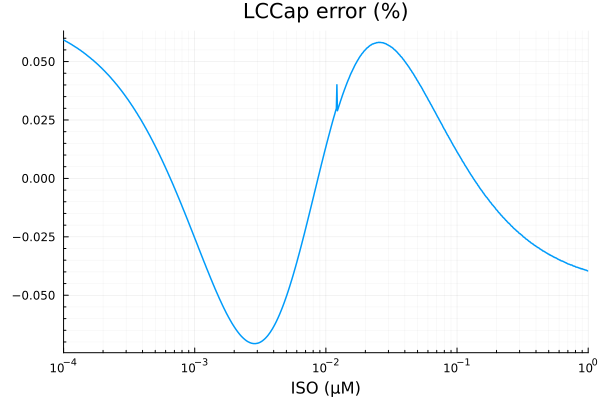
LCCbp
xdata = iso
ydata = extract(sim, sys.LCCbp / sys.LCCtotBA)
plot(xdata, ydata, title="LCCbp fraction", lab=false; xopts...)
p0 = [0.8, 1e-2μM, 0.1]
lb = [0.1, 1e-9μM, 0.0]
prob = NonlinearCurveFitProblem(model_lcc, p0, xdata, ydata)
@time fit_lccb = solve(prob) 0.001499 seconds (1.66 k allocations: 5.320 MiB)retcode: StalledSuccess
f: model_lcc
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 1.3974835275001972e-17
u: [0.24559084141313625, 0.0069612258074359095, 0.25200776506286443]println("LCCbp")
println("Basal activity: ", fit_lccb.u[3])
println("Activated activity: ", fit_lccb.u[1])
println("Michaelis constant: ", fit_lccb.u[2], " μM")
println("RMSE: ", mse(fit_lccb) |> sqrt)LCCbp
Basal activity: 0.25200776506286443
Activated activity: 0.24559084141313625
Michaelis constant: 0.0069612258074359095 μM
RMSE: 0.000138276524916985p1 = plot(xdata, [ydata predict(fit_lccb)], lab=["Full model" "Fitted"], line=[:dash :dot], title="LCCbp", legend=:topleft; xopts...)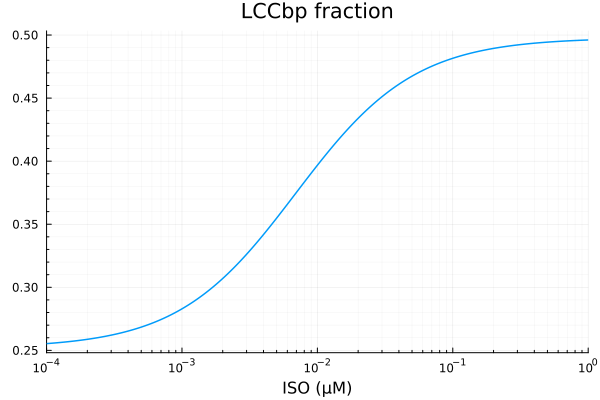
savefig("lccbp_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/lccbp_fit.pdf"plot(xdata, residuals(fit_lccb) ./ ydata .* 100; title="LCCbp error (%)", lab=false, xopts...)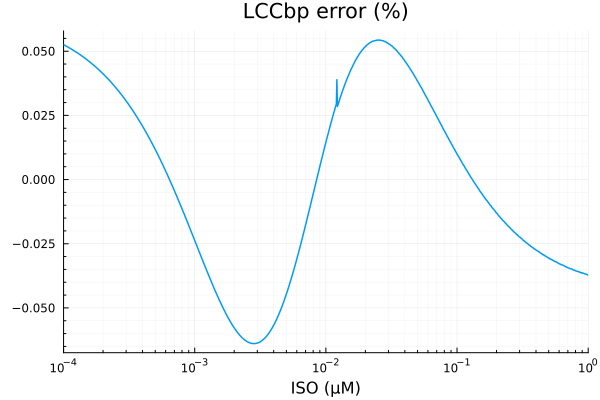
KURp
xdata = iso
ydata = extract(sim, sys.KURp / sys.IKurtotBA)
plot(xdata, ydata, title="KURp fraction", lab=false; xopts...)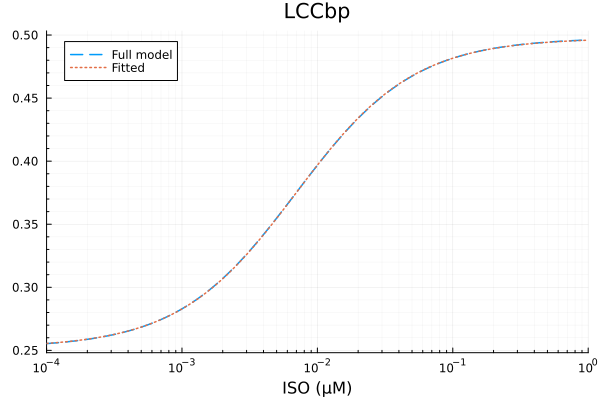
model_kur(p, x) = @. p[1] * hil(x, p[2]) + p[3]
p0 = [0.8, 1e-2μM, 0.1]
lb = [0.1, 1e-9μM, 0.0]
prob = NonlinearCurveFitProblem(model_kur, p0, xdata, ydata)
@time fit_kur = solve(prob) 1.620531 seconds (7.53 M allocations: 379.649 MiB, 2.93% gc time, 99.84% compilation time)retcode: StalledSuccess
f: model_kur
alg: __FallbackNonlinearFitAlgorithm
residuals mean: 7.891345474733255e-17
u: [0.25565887741346405, 0.005578225308158629, 0.4393637021585133]println("KURp")
println("Basal activity: ", fit_kur.u[3])
println("Activated activity: ", fit_kur.u[1])
println("Michaelis constant: ", fit_kur.u[2], " μM")
println("RMSE: ", mse(fit_kur) |> sqrt)KURp
Basal activity: 0.4393637021585133
Activated activity: 0.25565887741346405
Michaelis constant: 0.005578225308158629 μM
RMSE: 0.0001487454886433698p1 = plot(xdata, [ydata predict(fit_kur)], lab=["Full model" "Fitted"], line=[:dash :dot], title="KURp", legend=:topleft; xopts...)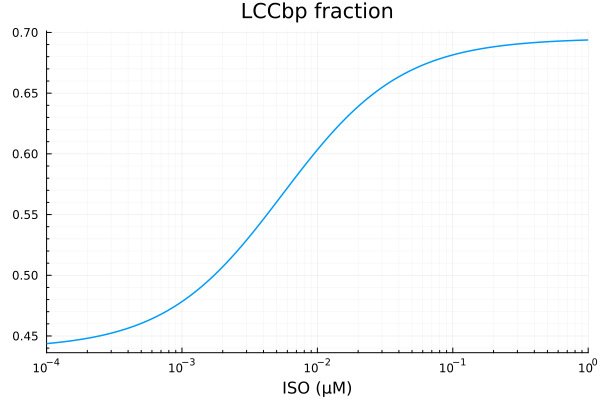
savefig("kurp_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/kurp_fit.pdf"p2 = plot(xdata, residuals(fit_kur) ./ ydata .* 100; title="KURp error (%)", lab=false, xopts...)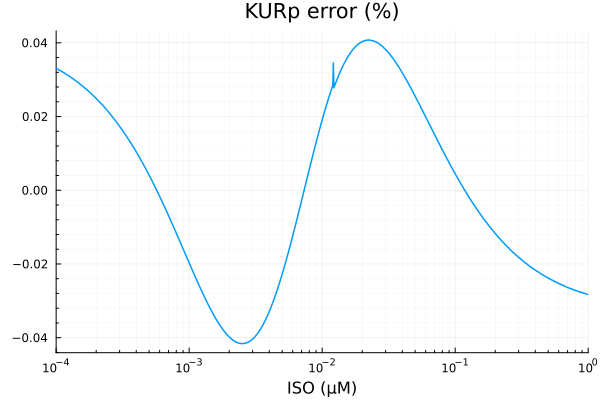
RyRp
xdata = iso
ydata = extract(sim, sys.RyR_PKAp)
plot(xdata, ydata, title="RyRp fraction", lab=false; xopts...)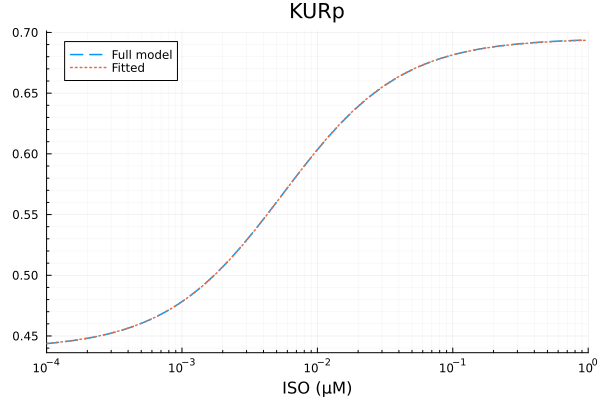
model(p, x) = @. p[1] * x / (x + p[2]) + p[3]
p0 = [0.3, 1e-2μM, 0.1]
lb = [0.0, 1e-9μM, 0.0]
prob = NonlinearCurveFitProblem(model, p0, xdata, ydata)
@time fit_ryr = solve(prob) 1.077766 seconds (3.94 M allocations: 193.877 MiB, 99.75% compilation time: 100% of which was recompilation)retcode: StalledSuccess
f: model
alg: __FallbackNonlinearFitAlgorithm
residuals mean: -1.3170727689733999e-17
u: [0.23988857454116702, 0.007509983438024364, 0.20539784110327894]println("RyRp")
println("Basal activity: ", fit_ryr.u[3])
println("Activated activity: ", fit_ryr.u[1])
println("Michaelis constant: ", fit_ryr.u[2], " μM")
println("RMSE: ", mse(fit_ryr) |> sqrt)RyRp
Basal activity: 0.20539784110327894
Activated activity: 0.23988857454116702
Michaelis constant: 0.007509983438024364 μM
RMSE: 7.696798893451903e-5p1 = plot(xdata, [ydata predict(fit_ryr)], lab=["Full model" "Fitted"], line=[:dash :dot], title="RyRp", legend=:topleft; xopts...)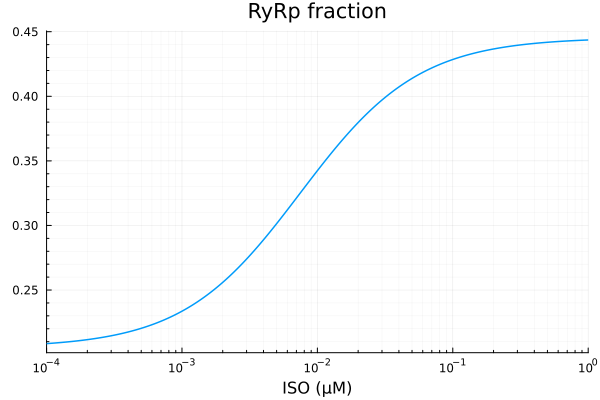
savefig("ryrp_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/ryrp_fit.pdf"p2 = plot(xdata, residuals(fit_ryr) ./ ydata .* 100; title="RyRp error (%)", lab=false, xopts...)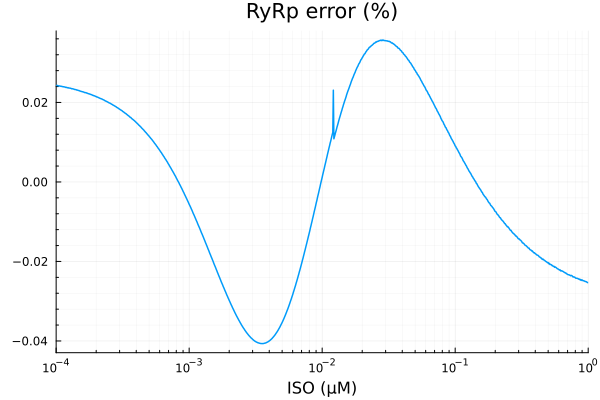
This notebook was generated using Literate.jl.