using ModelingToolkit
using OrdinaryDiffEq, SteadyStateDiffEq, DiffEqCallbacks
using Plots
using CurveFit
using CaMKIIModel
using CaMKIIModel: μM, hil, second, Hz
Plots.default(lw=1.5)CaMKII system simplification
CaMKII sensitivity to calcium
Modeling CaM-Cax binding to CaMKII only. No phosphorylation or oxidation reactions.
@parameters Ca = 0μM ROS = 0μM
@time "Build system" sys = get_camkii_sys(; Ca, ROS, simplify=true)
@time "Build problem" prob = SteadyStateProblem(sys, [sys.k_phosCaM => 0])Build system: 21.825230 seconds (44.27 M allocations: 2.156 GiB, 3.75% gc time, 99.60% compilation time: 57% of which was recompilation)
Build problem: 12.705772 seconds (38.20 M allocations: 1.897 GiB, 1.96% gc time, 99.59% compilation time: 59% of which was recompilation)SteadyStateProblem with uType Vector{Float64}. In-place: true u0: 17-element Vector{Float64}: 0.0 0.0 0.0 3.3 0.0 0.0 0.01581 0.010750000000000001 1.01 0.62372 0.00666 0.0166 0.39868000000000003 1.0 2.0e-5 0.008577999999999999 0.08433
Physiological cytosolic calcium concentrations ranges from 30nM to 10μM.
ca = logrange(0.03μM, 10μM, length=1001)
prob_func = (prob, i, repeat) -> (prob.ps[Ca] = ca[i]; prob)
alg = DynamicSS(KenCarp47())
sol0 = solve(prob, alg) ## warmup
@time "Solve problem" sim = solve(EnsembleProblem(prob; prob_func), alg; trajectories=length(ca))Solve problem: 6.480340 seconds (33.76 M allocations: 2.175 GiB, 22.78% gc time, 35.30% compilation time)EnsembleSolution Solution of length 1001 with uType:
SciMLBase.NonlinearSolution{_A, _B, _C, _D, SciMLBase.SteadyStateProblem{Vector{Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x4e59762c, 0x38ef17f0, 0xa1dcb1bb, 0xedf9a871, 0x537caa1b), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x1a79d783, 0x354b1477, 0xa45559a1, 0x89a221f9, 0x3f81ac1e), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xdddcfdeb, 0x34ea441c, 0x9d13c31f, 0xe0898c04, 0x1139e68d), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x33f8209c, 0xca3f1431, 0x785cf31d, 0xa154e4b6, 0x8371f0fb), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xb728062f, 0xac974193, 0xcfcfa36e, 0xffe50d14, 0x04cbeef0), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xf594c34c, 0x582ecb45, 0xb0f41e66, 0x965ba5bf, 0x7ecc0806), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x949bdd90, 0xaee9a3b6, 0x251c9a2f, 0x9c60f2b7, 0xd605c55d), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x8fc4dc42, 0xab19a0c7, 0x7dc77568, 0x6a4f78c4, 0xf2705f06), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}}, SteadyStateDiffEq.DynamicSS{_A1, Float64}, _E, Nothing, Nothing, Nothing} where {_A, _B, _C, _D, _A1, _E}"""Extract values from ensemble simulations by a symbol"""
extract(sim, k) = map(s -> s[k], sim)Main.var"##277".extractStatus of the CaMKII system across a range of calcium concentrations.
xopts = (xlabel="Ca (μM)", xscale=:log10, minorgrid=true, xlims=(ca[1], ca[end]))
let
plot(ca, extract(sim, sys.CaM0), lab="CaM0", ylabel="Conc. (μM)"; xopts...)
plot!(ca, extract(sim, sys.Ca2CaM_C), lab="Ca2CaM_C")
plot!(ca, extract(sim, sys.Ca2CaM_N), lab="Ca2CaM_N")
plot!(ca, extract(sim, sys.Ca4CaM), lab="Ca4CaM")
plot!(ca, extract(sim, sys.CaMK), lab="CaMK")
plot!(ca, extract(sim, sys.CaM0_CaMK), lab="CaM0_CaMK")
plot!(ca, extract(sim, sys.Ca2CaM_C_CaMK), lab="Ca2CaM_C_CaMK")
plot!(ca, extract(sim, sys.Ca2CaM_N_CaMK), lab="Ca2CaM_N_CaMK")
plot!(ca, extract(sim, sys.Ca4CaM_CaMK), lab="Ca4CaM_CaMK", legend=:topleft)
end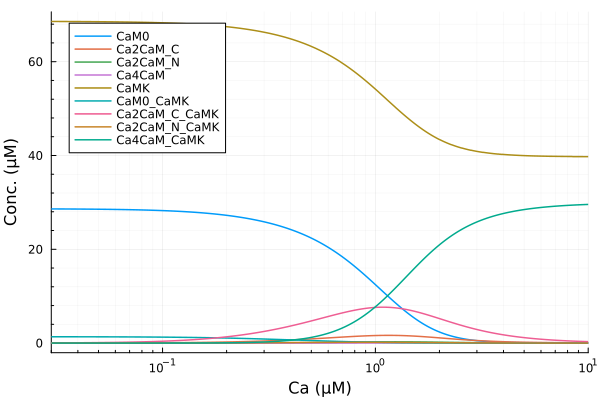
savefig("camkii_cam_binding.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/camkii_cam_binding.pdf"Active CaMKII is defined as CaMKII bound to CaMCax
CaMKAct = 1 - (sys.CaMK) / sys.CAMKII_T
println("Basal activity with 30nM Ca is ", sol0[CaMKAct][end])
xdata = ca
ydata = extract(sim, CaMKAct)
plot(xdata, ydata, label=false, title="Active CaMKII", ylims=(0, 0.5); xopts...)Basal activity with 30nM Ca is 0.019910346305831106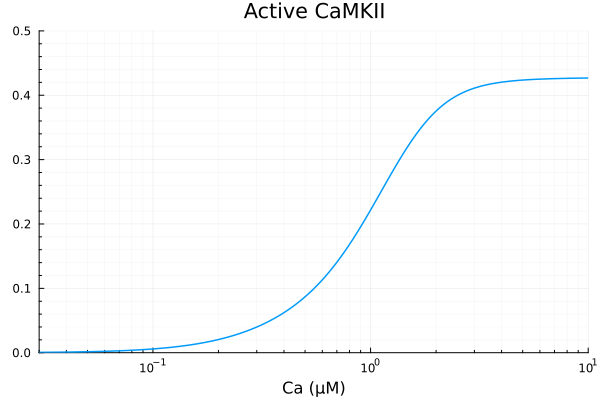
Least-square fitting
Least-square fitting of steady state CaMKII activities against calcium concentrations.
Old model
Using a single Hill function to fit steady state CaMKII activities.
\[ \text{CaMKII}_{act} = p_1 \frac{c^n}{c^n + p_2^n}+ p_3 \]
model_camk_single_hill(p, x) = @. p[1] * hil(x, p[2], p[4]) + p[3]
p0 = [0.4, 1μM, 0.0, 2.0]
prob = NonlinearCurveFitProblem(model_camk_single_hill, p0, xdata, ydata)
@time fit = solve(prob)
println("Basal activity: ", fit.u[3])
println("Maximal activated activity: ", fit.u[1])
println("Half-saturation Ca concentration: ", fit.u[2], " μM")
println("Hill coefficient: ", fit.u[4])
println("RMSE: ", mse(fit) |> sqrt) 4.655733 seconds (13.06 M allocations: 655.264 MiB, 1.87% gc time, 97.28% compilation time)
Basal activity: 0.024243888623769954
Maximal activated activity: 0.415136252066246
Half-saturation Ca concentration: 0.9933661013816575 μM
Hill coefficient: 2.373996903436689
RMSE: 0.004184835313473484Fit result and the original
plot(xdata, [ydata predict(fit)], lab=["Full model" "Fitted"], line=[:dash :dot], title="Single Hill function fit", legend=:topleft, ylabel="Bound CaMKII"; xopts...)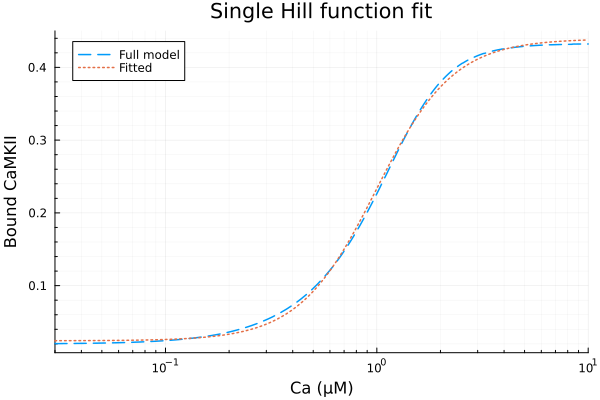
New model
Using two Hill functions to fit steady state CaMKII activities.
\[ \text{CaMKII}_{act} = p_1 \frac{c^2}{c^2 + p_2^2} + p_3 \frac{c^4}{c^4 + p_4^4} + p_5 \]
model_camk(p, x) = @. p[1] * hil(x, p[2], 2) + p[3] * hil(x, p[4], 4) + p[5]
p0 = [0.4, 1μM, 0.2, 1μM, 0.0]
prob = NonlinearCurveFitProblem(model_camk, p0, xdata, ydata)
@time fit = solve(prob)
println("Basal activity: ", fit.u[5])
println("Maximal activity by 2 Ca binding): ", fit.u[1])
println("Half saturation concentration for 2 Ca binding: ", fit.u[2], " μM")
println("Maximal activity by 4 Ca binding): ", fit.u[3])
println("Half saturation concentration for 4 Ca binding: ", fit.u[4], " μM")
println("RMSE: ", mse(fit) |> sqrt) 2.971608 seconds (8.56 M allocations: 429.234 MiB, 1.51% gc time, 99.66% compilation time)
Basal activity: 0.020233348338853496
Maximal activity by 2 Ca binding): 0.2554938435641706
Half saturation concentration for 2 Ca binding: 0.7889283569738373 μM
Maximal activity by 4 Ca binding): 0.15981014947977254
Half saturation concentration for 4 Ca binding: 1.2433691417644253 μM
RMSE: 0.0008772212630840381plot(xdata, [ydata predict(fit)], lab=["Full model" "Fitted"], line=[:dash :dot], title="Dual Hill function fit", legend=:topleft, ylabel="Bound CaMKII"; xopts...)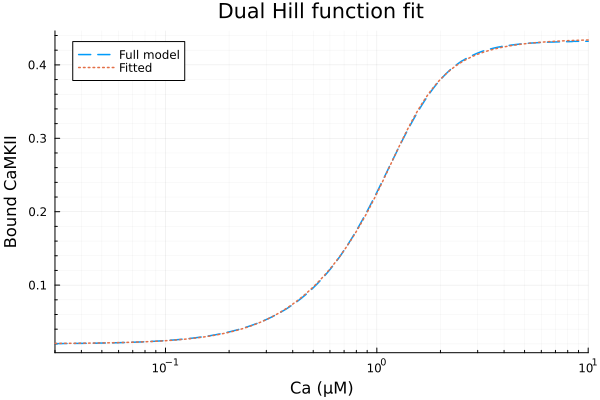
savefig("camkii_act_fit.pdf")"/home/github/actions-runner-1/_work/camkii-cardiomyocyte-model/camkii-cardiomyocyte-model/docs/camkii_act_fit.pdf"Polynomial fitting
prob = CurveFitProblem(xdata, ydata)
alg = RationalPolynomialFitAlgorithm(num_degree=2, den_degree=2)
@time sol = solve(prob, alg)
println("Numerator coefficients: ", sol.u[1:3])
println("Denominator coefficients: ", vcat(1.0, sol.u[4:5]))
println("RMSE: ", mse(sol) |> sqrt) 3.715898 seconds (11.50 M allocations: 574.455 MiB, 1.19% gc time, 99.75% compilation time)
Numerator coefficients: [0.019698109457797642, 0.01894054685488822, 0.2710015785533003]
Denominator coefficients: [1.0, -0.3058785858244601, 0.6599504905412737]
RMSE: 0.0017531040640622272plot(xdata, [ydata sol.(xdata)], lab=["Full model" "Fitted"], line=[:dash :dot], title="Rational polynomial fit", legend=:topleft, ylabel="Bound CaMKII"; xopts...)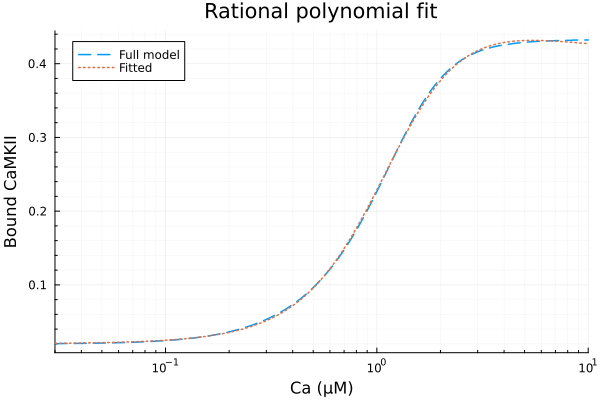
This notebook was generated using Literate.jl.