Calcium overload

Calcium overload#

Steady-state solutions across a range of glucose levels.

using OrdinaryDiffEq
using SteadyStateDiffEq
using ModelingToolkit
using MitochondrialDynamics
using MitochondrialDynamics: μM
import PythonPlot as plt
plt.matplotlib.rcParams["font.size"] = 14

Default model

@named sys = make_model()
prob = SteadyStateProblem(sys, [])
alg = DynamicSS(Rodas5())
sol = solve(prob, alg)

retcode: Success
u: 9-element Vector{Float64}:
05007786837364594
0008000956847624287
00019466055321005286
08901096138926226
0024720687731564486
00679879039097767
536585932057042
24242296954929593
05710335793593592

High calcium model

@unpack RestingCa, ActivatedCa = sys
prob_ca5 = SteadyStateProblem(sys, [], [RestingCa=>0.45μM, ActivatedCa=>1.25μM])
prob_ca10 = SteadyStateProblem(sys, [], [RestingCa=>0.9μM, ActivatedCa=>2.5μM])

SteadyStateProblem with uType Vector{Float64}. In-place: true
u0: 9-element Vector{Float64}:
057
001
0002
092
0029
0087
9
24
06

Simulating on a range of glucose

@unpack Glc = sys

\[\begin{split} \begin{align} \frac{\mathrm{d} \mathtt{NADH\_m}\left( t \right)}{\mathrm{d}t} &= \frac{\mathtt{J\_DH}\left( t \right) + \mathtt{J\_NADHT}\left( t \right) - \mathtt{J\_O2}\left( t \right)}{\mathtt{V\_MTX}} - \mathtt{kNADHm} \mathtt{NADH\_m}\left( t \right) \\ \frac{\mathrm{d} \mathtt{NADH\_c}\left( t \right)}{\mathrm{d}t} &= \frac{ - \mathtt{J\_LDH}\left( t \right) - \mathtt{J\_NADHT}\left( t \right) + \mathtt{J\_GPD}\left( t \right)}{\mathtt{V\_I}} - \mathtt{kNADHc} \mathtt{NADH\_c}\left( t \right) \\ \frac{\mathrm{d} \mathtt{Ca\_m}\left( t \right)}{\mathrm{d}t} &= \frac{\mathtt{F\_M} \left( \mathtt{J\_MCU}\left( t \right) - \mathtt{J\_NCLX}\left( t \right) \right)}{\mathtt{V\_MTX}} \\ \frac{\mathrm{d} \mathtt{\Delta{\Psi}m}\left( t \right)}{\mathrm{d}t} &= \frac{ - 2 \mathtt{J\_MCU}\left( t \right) + \mathtt{J\_HR}\left( t \right) - \mathtt{J\_HL}\left( t \right) - \mathtt{J\_HF}\left( t \right) - \mathtt{J\_ANT}\left( t \right)}{\mathtt{C\_MIT}} \\ \frac{\mathrm{d} \mathtt{G3P}\left( t \right)}{\mathrm{d}t} &= \frac{ - \mathtt{J\_GPD}\left( t \right) + 2 \mathtt{J\_GK}\left( t \right)}{\mathtt{V\_I}} - \mathtt{kG3P} \mathtt{G3P}\left( t \right) \\ \frac{\mathrm{d} \mathtt{Pyr}\left( t \right)}{\mathrm{d}t} &= \frac{ - \mathtt{J\_LDH}\left( t \right) - \mathtt{J\_PDH}\left( t \right) + \mathtt{J\_GPD}\left( t \right)}{\mathtt{V\_I} + \mathtt{V\_MTX}} - \mathtt{kPyr} \mathtt{Pyr}\left( t \right) \\ \frac{\mathrm{d} \mathtt{AEC}\left( t \right)}{\mathrm{d}t} &= \frac{\mathtt{J\_ANT}\left( t \right) + 2 \mathtt{J\_GPD}\left( t \right) - \mathtt{ATPstiochGK} \mathtt{J\_GK}\left( t \right) + \left( - \mathtt{kATP} - \mathtt{kATPCa} \mathtt{Ca\_c}\left( t \right) \right) \mathtt{ATP\_c}\left( t \right)}{\mathtt{V\_I} \mathtt{{\Sigma}Ac}} \\ \frac{\mathrm{d} \mathtt{x2}\left( t \right)}{\mathrm{d}t} &= - \mathtt{tipside}\left( t \right) + \mathtt{tiptip}\left( t \right) \\ \frac{\mathrm{d} \mathtt{x3}\left( t \right)}{\mathrm{d}t} &= \mathtt{tipside}\left( t \right) \end{align} \end{split}\]

Test on a range of glucose

glc = 3.5:0.5:30.0
prob_func = (prob, i, repeat) -> begin
    remake(prob, p=[Glc => glc[i]])
end

trajectories=length(glc)

sim = solve(EnsembleProblem(prob; prob_func, safetycopy=false), alg; trajectories)
sim_ca5 = solve(EnsembleProblem(prob_ca5; prob_func, safetycopy=false), alg; trajectories)
sim_ca10 = solve(EnsembleProblem(prob_ca10; prob_func, safetycopy=false), alg; trajectories);

Steady states for a range of glucose#

function plot_steady_state(glc, sols, sys; figsize=(10, 10), title="")

    @unpack G3P, Pyr, Ca_c, Ca_m, NADH_c, NADH_m, NAD_c, NAD_m, ATP_c, ADP_c, AMP_c, ΔΨm, x1, x2, x3, degavg = sys

    glc5 = glc ./ 5
    g3p = extract(sols, G3P * 1000)
    pyr = extract(sols, Pyr * 1000)
    ca_c = extract(sols, Ca_c * 1000)
    ca_m = extract(sols, Ca_m * 1000)
    nad_ratio_c = extract(sols, NADH_c/NAD_c)
    nad_ratio_m = extract(sols, NADH_m/NAD_m)
    atp_c = extract(sols, ATP_c * 1000)
    adp_c = extract(sols, ADP_c * 1000)
    amp_c = extract(sols, AMP_c * 1000)
    td = extract(sols, ATP_c / ADP_c)
    dpsi = extract(sols, ΔΨm * 1000)
    x1 = extract(sols, x1)
    x2 = extract(sols, x2)
    x3 = extract(sols, x3)
    deg = extract(sols, degavg)

    numrows = 3
    numcols = 3

    fig, ax = plt.subplots(numrows, numcols; figsize)

    ax[0, 0].plot(glc5, g3p)
    ax[0, 0].set(ylabel="G3P (μM)")
    ax[0, 0].set_title("a", loc="left")
    ax[0, 1].plot(glc5, pyr)
    ax[0, 1].set(ylabel="Pyruvate (μM)")
    ax[0, 1].set_title("b", loc="left")
    ax[0, 2].plot(glc5, ca_c, label="cyto")
    ax[0, 2].plot(glc5, ca_m, label="mito")
    ax[0, 2].legend()
    ax[0, 2].set(ylabel="Calcium (μM)")
    ax[0, 2].set_title("c", loc="left")
    ax[1, 0].plot(glc5, nad_ratio_c, label="cyto")
    ax[1, 0].plot(glc5, nad_ratio_m, label="mito")
    ax[1, 0].legend()
    ax[1, 0].set(ylabel="NADH:NAD (ratio)")
    ax[1, 0].set_title("d", loc="left")
    ax[1, 1].plot(glc5, atp_c, label="ATP")
    ax[1, 1].plot(glc5, adp_c, label="ADP")
    ax[1, 1].plot(glc5, amp_c, label="AMP")
    ax[1, 1].legend()
    ax[1, 1].set(ylabel="Adenylates (μM)")
    ax[1, 1].set_title("e", loc="left")
    ax[1, 2].plot(glc5, td)
    ax[1, 2].set(ylabel="ATP:ADP (ratio)")
    ax[1, 2].set_title("f", loc="left")
    ax[2, 0].plot(glc5, dpsi, label="cyto")
    ax[2, 0].set(ylabel="ΔΨ (mV)", xlabel="Glucose (X)")
    ax[2, 0].set_title("g", loc="left")
    ax[2, 1].plot(glc5, x1, label="X1")
    ax[2, 1].plot(glc5, x2, label="X2")
    ax[2, 1].plot(glc5, x3, label="X3")
    ax[2, 1].set(ylabel="Mitochondrial nodes (a.u.)", xlabel="Glucose (X)")
    ax[2, 1].set_title("h", loc="left")
    ax[2, 2].plot(glc5, deg)
    ax[2, 2].set(ylabel="Avg. Node Degree (a.u.)", xlabel="Glucose (X)")
    ax[2, 2].set_title("i", loc="left")

    for i in 0:numrows-1, j in 0:numcols-1
        ax[i, j].set_xticks(1:6)
        ax[i, j].grid()
    end
    fig.suptitle(title)
    fig.tight_layout()
    return fig
end

plot_steady_state (generic function with 1 method)

Default model

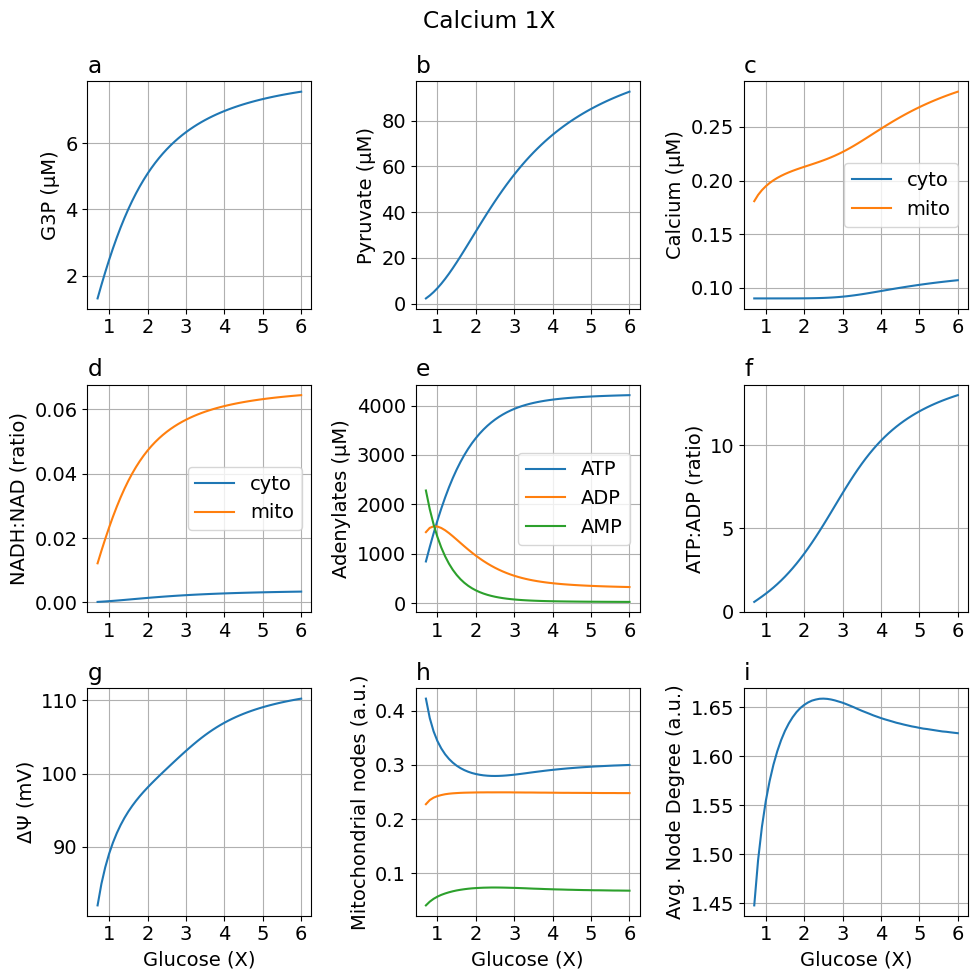
fig_glc_default = plot_steady_state(glc, sim, sys, title="Calcium 1X")

_images/b74ddae8f158bd4f4e331bc4e61f64b112a07eedfb4f8bdd61b2a2d3b807e15a.png

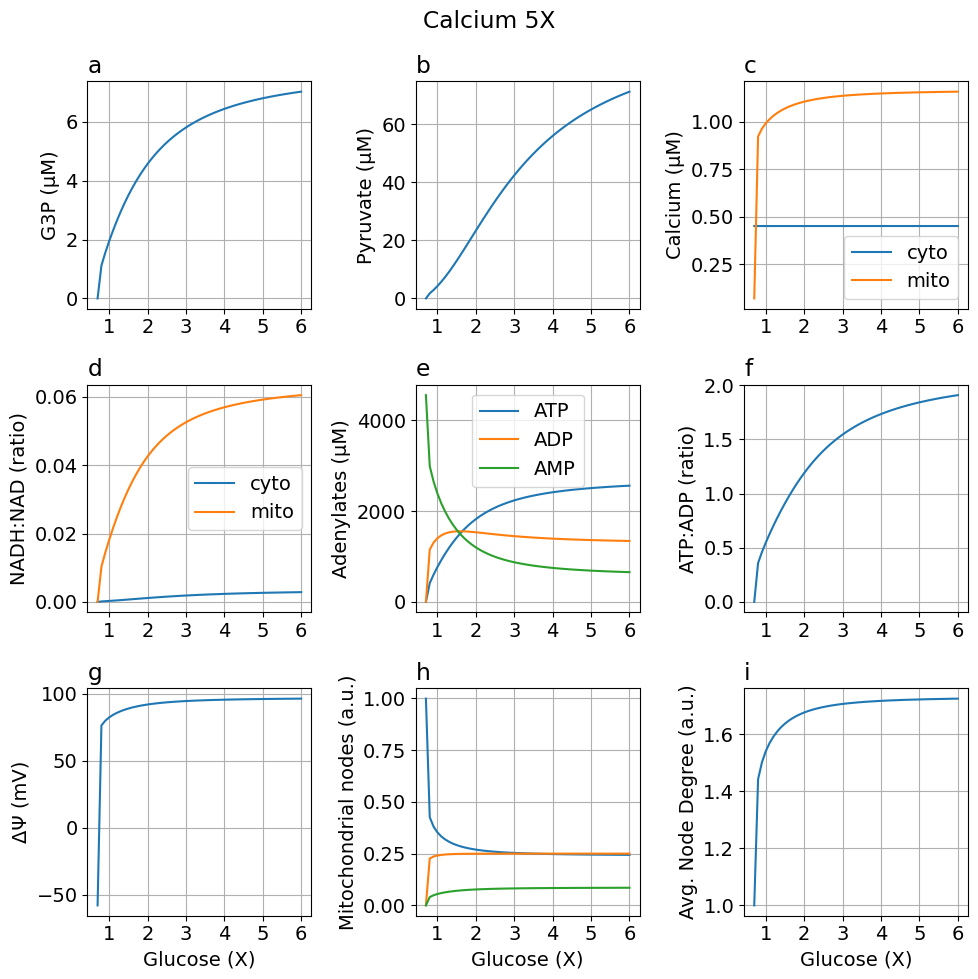
High calcium (5X)

fig_ca5 = plot_steady_state(glc, sim_ca5, sys, title="Calcium 5X")

_images/d5a7e430fb1b2e7c79dd6bf5f6b33bef79f2190cbf3febe9f6439a020f7e90c8.png

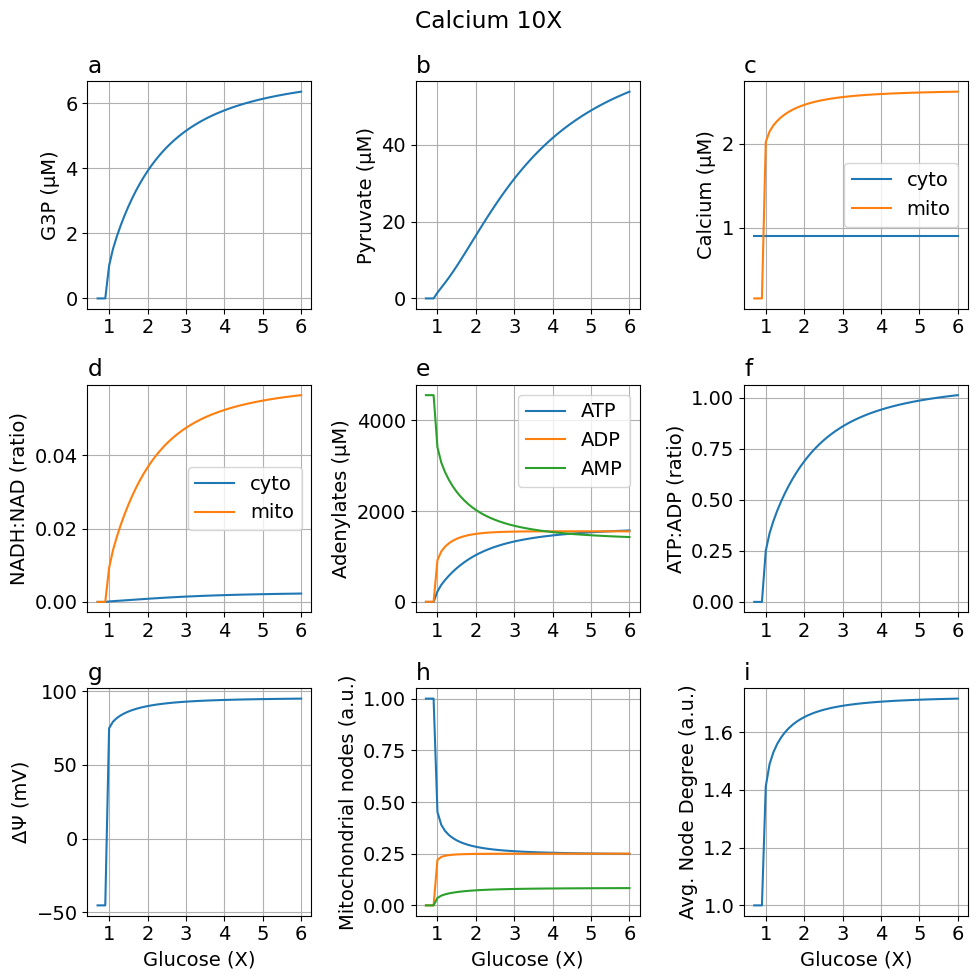
High calcium (10X)

fig_ca10 = plot_steady_state(glc, sim_ca10, sys, title="Calcium 10X")

_images/d507d55ba8b3935a69bef1be266e77c5b5ee238d164c675836ff78016deee7aa.png

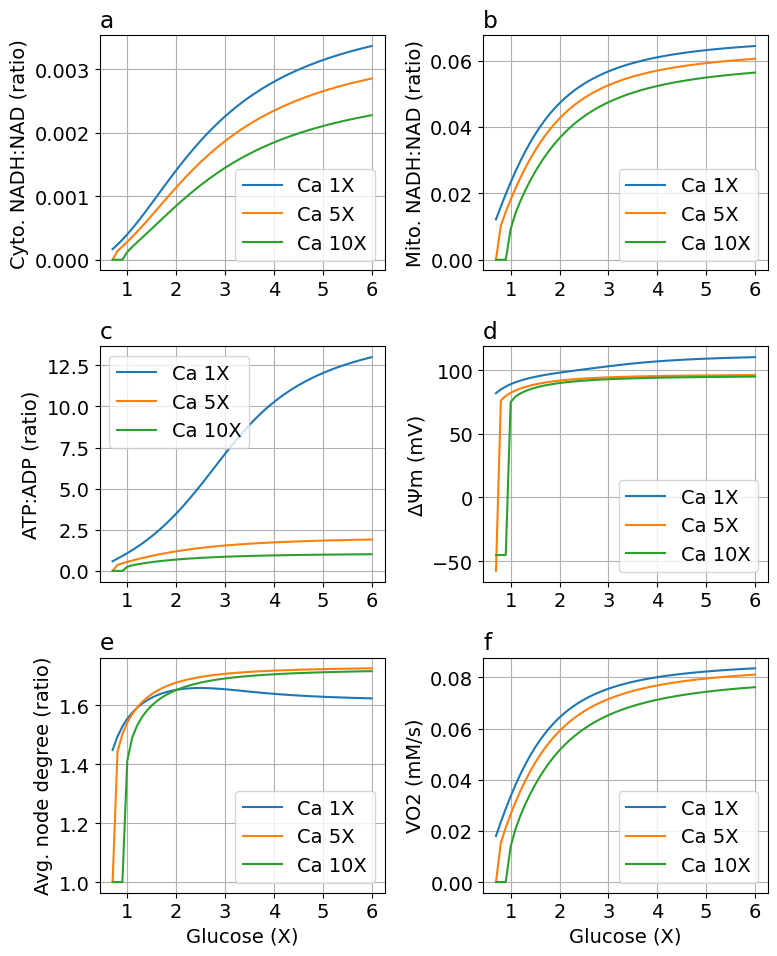
Comparing default and high calcium models#

function plot_comparision(glc, sim, sim_ca5, sim_ca10, sys;
    figsize=(8, 10), title="", labels=["Ca 1X", "Ca 5X", "Ca 10X"]
)
    @unpack G3P, Pyr, Ca_c, Ca_m, NADH_c, NADH_m, NAD_c, NAD_m, ATP_c, ADP_c, AMP_c, ΔΨm, degavg, J_O2 = sys

    glc5 = glc ./ 5

    numrows = 3
    numcols = 2
    fig, ax = plt.subplots(numrows, numcols; figsize)

    ax[0, 0].set_title("a", loc="left")
    ax[0, 0].set_ylabel("Cyto. NADH:NAD (ratio)")
    k = NADH_c/NAD_c
    yy = [extract(sim, k) extract(sim_ca5, k) extract(sim_ca10, k)]
    lines = ax[0, 0].plot(glc5, yy)
    ax[0, 0].legend(lines, labels)

    ax[0, 1].set_title("b", loc="left")
    ax[0, 1].set_ylabel("Mito. NADH:NAD (ratio)")
    k = NADH_m/NAD_m
    yy = [extract(sim, k) extract(sim_ca5, k) extract(sim_ca10, k)]
    lines = ax[0, 1].plot(glc5, yy)
    ax[0, 1].legend(lines, labels)

    ax[1, 0].set_title("c", loc="left")
    ax[1, 0].set_ylabel("ATP:ADP (ratio)")
    k = ATP_c/ADP_c
    yy = [extract(sim, k) extract(sim_ca5, k) extract(sim_ca10, k)]
    lines = ax[1, 0].plot(glc5, yy)
    ax[1, 0].legend(lines, labels)

    ax[1, 1].set_title("d", loc="left")
    ax[1, 1].set_ylabel("ΔΨm (mV)")
    k = ΔΨm * 1000
    yy = [extract(sim, k) extract(sim_ca5, k) extract(sim_ca10, k)]
    lines = ax[1, 1].plot(glc5, yy)
    ax[1, 1].legend(lines, labels)

    ax[2, 0].set_title("e", loc="left")
    ax[2, 0].set_ylabel("Avg. node degree (ratio)")
    k = degavg
    yy = [extract(sim, k) extract(sim_ca5, k) extract(sim_ca10, k)]
    lines = ax[2, 0].plot(glc5, yy)
    ax[2, 0].legend(lines, labels, loc="lower right")
    ax[2, 0].set(xlabel="Glucose (X)")

    ax[2, 1].set_title("f", loc="left")
    ax[2, 1].set_ylabel("VO2 (mM/s)")
    k = J_O2
    yy = [extract(sim, k) extract(sim_ca5, k) extract(sim_ca10, k)]
    lines = ax[2, 1].plot(glc5, yy)
    ax[2, 1].legend(lines, labels)
    ax[2, 1].set(xlabel="Glucose (X)")

    for i in 0:numrows-1, j in 0:numcols-1
        ax[i, j].set_xticks(1:6)
        ax[i, j].grid()
    end

    fig.suptitle(title)
    fig.tight_layout()
    return fig
end

figcomp = plot_comparision(glc, sim, sim_ca5, sim_ca10, sys)

_images/f2d59fa37bcedf0dc4d93073e3a4b5326184d89c17ae4c1c8a29400c715f5085.png

Export figure

exportTIF(figcomp, "S1_HighCa.tif")

Python: None

MMP vs #

function plot_dpsi_k(sim, sim_ca5, sim_ca10, sys; figsize=(6,6), title="", labels=["Ca 1X", "Ca 5X", "Ca 10X"])
    @unpack ΔΨm, degavg = sys

    fig, ax = plt.subplots(1, 1; figsize)

    ax.plot(extract(sim, ΔΨm * 1000), extract(sim, degavg), "v", label=labels[1])
    ax.plot(extract(sim_ca5, ΔΨm * 1000), extract(sim_ca5, degavg), "o", label=labels[2])
    ax.plot(extract(sim_ca10, ΔΨm * 1000), extract(sim_ca10, degavg), "x", label=labels[3])
    ax.set(xlabel="ΔΨm (mV)", ylabel="Average node degree", title=title)
    ax.legend()
    ax.grid()

    return fig
end

fig = plot_dpsi_k(sim, sim_ca5, sim_ca10, sys)

_images/c03fb1314479890a38ef4cf66847c8b4068c2daed38890ddffddcc342465594a.png

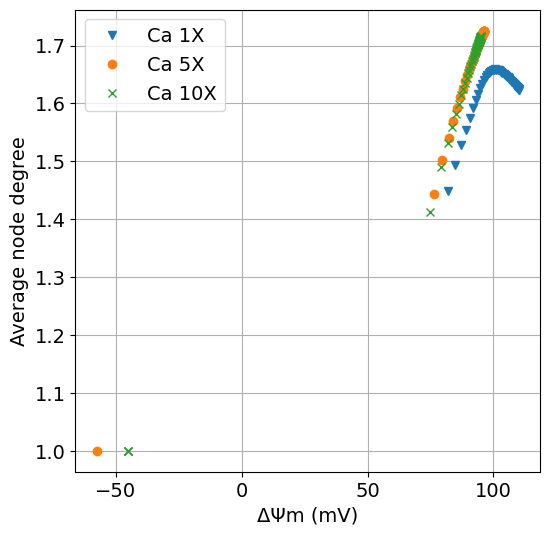
# exportTIF(fig, "S1_HighCa_dpsi_k.tif")

x-axis as Ca2+ and y-axis as average node degree#

function plot_ca_k(sim, sim_ca5, sim_ca10, sys; figsize=(6,6), title="", labels=["Ca 1X", "Ca 5X", "Ca 10X"])
    @unpack Ca_m, degavg = sys

    fig, ax = plt.subplots(1, 1; figsize)

    ax.plot(extract(sim, Ca_m * 1000), extract(sim, degavg), "v", label=labels[1])
    ax.plot(extract(sim_ca5, Ca_m * 1000), extract(sim_ca5, degavg), "o", label=labels[2])
    ax.plot(extract(sim_ca10, Ca_m * 1000), extract(sim_ca10, degavg), "x", label=labels[3])
    ax.set(xlabel="Mitochondrial Ca (mM)", ylabel="Average node degree", title=title)
    ax.legend()
    ax.grid()
    return fig
end

fig = plot_ca_k(sim, sim_ca5, sim_ca10, sys)

_images/321952cca012c16353696416986fad4b42b25002ecb9bef53d34c8e58d93c443.png

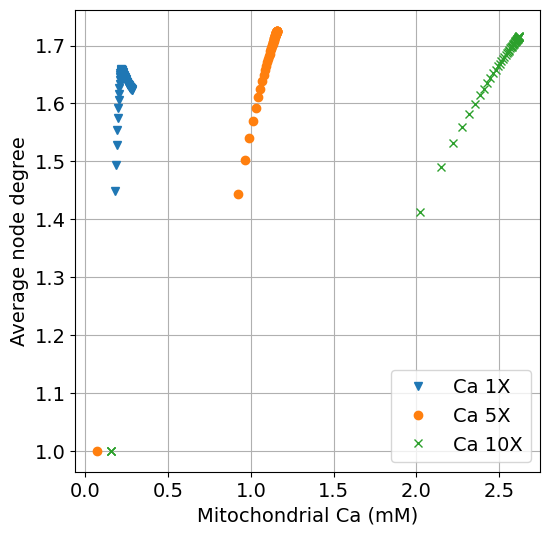
exportTIF(fig, "S1_HighCa_ca_k.tif")

Python: None

x-axis as ATP and y-axis as average node degree#

function plot_atp_k(sim, sim_ca5, sim_ca10, sys; figsize=(6,6), title="", labels=["Ca 1X", "Ca 5X", "Ca 10X"])
    @unpack ATP_c, ADP_c, degavg = sys

    k = ATP_c / ADP_c

    fig, ax = plt.subplots(1, 1; figsize)

    ax.plot(extract(sim, k), extract(sim, degavg), "v", label=labels[1])
    ax.plot(extract(sim_ca5, k), extract(sim_ca5, degavg), "o", label=labels[2])
    ax.plot(extract(sim_ca10, k), extract(sim_ca10, degavg), "x", label=labels[3])
    ax.set(xlabel="ATP:ADP ratio", ylabel="Average node degree", title=title)
    ax.legend()
    ax.grid()

    return fig
end

fig = plot_atp_k(sim, sim_ca5, sim_ca10, sys)

_images/a5465b9f90adbe4d3e560af3ee179a46ff07b9db56a663cff6a10b1943b32bda.png

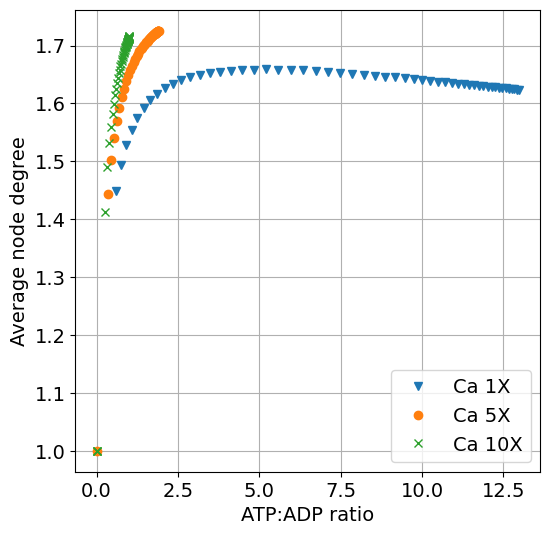
exportTIF(fig, "S1_HighCa_atp_k.tif")

Python: None

This notebook was generated using Literate.jl.