using ModelingToolkit
using NonlinearSolve
using OrdinaryDiffEq
using SteadyStateDiffEq
using Plots
using NaNMath
using ECMEDox: iVT, mV, μM, mM, Molar, HzComplex I model
Comparing Gauthier, Markevich, and simplified complex I models.
Candidates
Gauthier 2012
Gauthier 2012 7-state QSSA model
function c1_gauthier(; name=:c1gauthier,
Q_n=1800μM, QH2_n=200μM, nad=500μM, nadh=500μM,
dpsi=150mV, O2=6μM, sox_m=0.01μM,
h_i=exp10(-7) * Molar, h_m=exp10(-7.6) * Molar,
C1_INHIB=1)
@independent_variables t
D = Differential(t)
@parameters begin
ET_C1 = 8.85mM ## Activity of complex I
dpsi_B_C1 = 50mV ## Phase boundary potential
# Transition rates
K12_C1 = 6.3396E11Hz / mM^2
K21_C1 = 5Hz
K56_C1 = 100Hz
K65_C1 = 2.5119E13Hz / mM^2
K61_C1 = 1e7Hz
K16_C1 = 130Hz
K23_C1 = 3886.7Hz / sqrt(mM)
K32_C1 = 9.1295e6Hz
K34_C1 = 639.1364Hz
K43_C1 = 3.2882Hz / sqrt(mM)
K47_C1 = 1.5962E7Hz / mM
K74_C1 = 65.2227Hz
K75_C1 = 24615Hz
K57_C1 = 1166.7Hz / sqrt(mM)
K42_C1 = 6.0318Hz / mM
Em_O2_SOX = -160mV ## O2/Superoxide redox potential
Em_FMNH2_FMNH = -375mV ## FMNH/FMNH2 redox potential
rKEQ_ROS_C1 = exp(iVT * (Em_FMNH2_FMNH - Em_O2_SOX))
end
@variables begin
C1_1(t)
C1_2(t)
C1_3(t)
C1_4(t)
C1_5(t)
C1_6(t)
C1_7(t)
wC1_1(t)
wC1_2(t)
wC1_3(t)
wC1_4(t)
wC1_5(t)
wC1_6(t)
wC1_7(t)
vQC1(t)
vNADHC1(t)
vROSC1(t)
vHresC1(t)
TNC1(t) ## Turnover number
end
fv = exp(iVT * (dpsi - dpsi_B_C1))
# State transition rates
a12 = K12_C1 * h_m^2
a21 = K21_C1
a65 = K65_C1 * h_i^2
a56 = K56_C1
a61 = K61_C1 / fv
a16 = K16_C1 * fv
a23 = K23_C1 * NaNMath.sqrt(nadh)
a32 = K32_C1
a34 = K34_C1
a43 = K43_C1 * NaNMath.sqrt(nad)
a47 = C1_INHIB * K47_C1 * NaNMath.sqrt(Q_n * h_m)
a74 = K74_C1
a57 = C1_INHIB * K57_C1 * NaNMath.sqrt(QH2_n)
a75 = K75_C1
a42 = K42_C1 * O2
a24 = K42_C1 * rKEQ_ROS_C1 * sox_m
# KA pattern
w1 = a21 * a32 * a42 * a56 * a61 * a74 + a21 * a32 * a42 * a56 * a61 * a75 + a21 * a32 * a42 * a57 * a61 * a74 + a21 * a32 * a42 * a57 * a65 * a74 + a21 * a32 * a43 * a56 * a61 * a74 + a21 * a32 * a43 * a56 * a61 * a75 + a21 * a32 * a43 * a57 * a61 * a74 + a21 * a32 * a43 * a57 * a65 * a74 + a21 * a32 * a47 * a56 * a61 * a75 + a21 * a34 * a42 * a56 * a61 * a74 + a21 * a34 * a42 * a56 * a61 * a75 + a21 * a34 * a42 * a57 * a61 * a74 + a21 * a34 * a42 * a57 * a65 * a74 + a21 * a34 * a47 * a56 * a61 * a75 + a23 * a34 * a47 * a56 * a61 * a75 + a24 * a32 * a47 * a56 * a61 * a75 + a24 * a34 * a47 * a56 * a61 * a75
w2 = a12 * a32 * a42 * a56 * a61 * a74 + a12 * a32 * a42 * a56 * a61 * a75 + a12 * a32 * a42 * a57 * a61 * a74 + a12 * a32 * a42 * a57 * a65 * a74 + a12 * a32 * a43 * a56 * a61 * a74 + a12 * a32 * a43 * a56 * a61 * a75 + a12 * a32 * a43 * a57 * a61 * a74 + a12 * a32 * a43 * a57 * a65 * a74 + a12 * a32 * a47 * a56 * a61 * a75 + a12 * a34 * a42 * a56 * a61 * a74 + a12 * a34 * a42 * a56 * a61 * a75 + a12 * a34 * a42 * a57 * a61 * a74 + a12 * a34 * a42 * a57 * a65 * a74 + a12 * a34 * a47 * a56 * a61 * a75 + a16 * a32 * a42 * a57 * a65 * a74 + a16 * a32 * a43 * a57 * a65 * a74 + a16 * a34 * a42 * a57 * a65 * a74
w3 = a12 * a23 * a42 * a56 * a61 * a74 + a12 * a23 * a42 * a56 * a61 * a75 + a12 * a23 * a42 * a57 * a61 * a74 + a12 * a23 * a42 * a57 * a65 * a74 + a12 * a23 * a43 * a56 * a61 * a74 + a12 * a23 * a43 * a56 * a61 * a75 + a12 * a23 * a43 * a57 * a61 * a74 + a12 * a23 * a43 * a57 * a65 * a74 + a12 * a23 * a47 * a56 * a61 * a75 + a12 * a24 * a43 * a56 * a61 * a74 + a12 * a24 * a43 * a56 * a61 * a75 + a12 * a24 * a43 * a57 * a61 * a74 + a12 * a24 * a43 * a57 * a65 * a74 + a16 * a21 * a43 * a57 * a65 * a74 + a16 * a23 * a42 * a57 * a65 * a74 + a16 * a23 * a43 * a57 * a65 * a74 + a16 * a24 * a43 * a57 * a65 * a74
w4 = a12 * a23 * a34 * a56 * a61 * a74 + a12 * a23 * a34 * a56 * a61 * a75 + a12 * a23 * a34 * a57 * a61 * a74 + a12 * a23 * a34 * a57 * a65 * a74 + a12 * a24 * a32 * a56 * a61 * a74 + a12 * a24 * a32 * a56 * a61 * a75 + a12 * a24 * a32 * a57 * a61 * a74 + a12 * a24 * a32 * a57 * a65 * a74 + a12 * a24 * a34 * a56 * a61 * a74 + a12 * a24 * a34 * a56 * a61 * a75 + a12 * a24 * a34 * a57 * a61 * a74 + a12 * a24 * a34 * a57 * a65 * a74 + a16 * a21 * a32 * a57 * a65 * a74 + a16 * a21 * a34 * a57 * a65 * a74 + a16 * a23 * a34 * a57 * a65 * a74 + a16 * a24 * a32 * a57 * a65 * a74 + a16 * a24 * a34 * a57 * a65 * a74
w5 = a12 * a23 * a34 * a47 * a61 * a75 + a12 * a23 * a34 * a47 * a65 * a75 + a12 * a24 * a32 * a47 * a61 * a75 + a12 * a24 * a32 * a47 * a65 * a75 + a12 * a24 * a34 * a47 * a61 * a75 + a12 * a24 * a34 * a47 * a65 * a75 + a16 * a21 * a32 * a42 * a65 * a74 + a16 * a21 * a32 * a42 * a65 * a75 + a16 * a21 * a32 * a43 * a65 * a74 + a16 * a21 * a32 * a43 * a65 * a75 + a16 * a21 * a32 * a47 * a65 * a75 + a16 * a21 * a34 * a42 * a65 * a74 + a16 * a21 * a34 * a42 * a65 * a75 + a16 * a21 * a34 * a47 * a65 * a75 + a16 * a23 * a34 * a47 * a65 * a75 + a16 * a24 * a32 * a47 * a65 * a75 + a16 * a24 * a34 * a47 * a65 * a75
w6 = a12 * a23 * a34 * a47 * a56 * a75 + a12 * a24 * a32 * a47 * a56 * a75 + a12 * a24 * a34 * a47 * a56 * a75 + a16 * a21 * a32 * a42 * a56 * a74 + a16 * a21 * a32 * a42 * a56 * a75 + a16 * a21 * a32 * a42 * a57 * a74 + a16 * a21 * a32 * a43 * a56 * a74 + a16 * a21 * a32 * a43 * a56 * a75 + a16 * a21 * a32 * a43 * a57 * a74 + a16 * a21 * a32 * a47 * a56 * a75 + a16 * a21 * a34 * a42 * a56 * a74 + a16 * a21 * a34 * a42 * a56 * a75 + a16 * a21 * a34 * a42 * a57 * a74 + a16 * a21 * a34 * a47 * a56 * a75 + a16 * a23 * a34 * a47 * a56 * a75 + a16 * a24 * a32 * a47 * a56 * a75 + a16 * a24 * a34 * a47 * a56 * a75
w7 = a12 * a23 * a34 * a47 * a56 * a61 + a12 * a23 * a34 * a47 * a57 * a61 + a12 * a23 * a34 * a47 * a57 * a65 + a12 * a24 * a32 * a47 * a56 * a61 + a12 * a24 * a32 * a47 * a57 * a61 + a12 * a24 * a32 * a47 * a57 * a65 + a12 * a24 * a34 * a47 * a56 * a61 + a12 * a24 * a34 * a47 * a57 * a61 + a12 * a24 * a34 * a47 * a57 * a65 + a16 * a21 * a32 * a42 * a57 * a65 + a16 * a21 * a32 * a43 * a57 * a65 + a16 * a21 * a32 * a47 * a57 * a65 + a16 * a21 * a34 * a42 * a57 * a65 + a16 * a21 * a34 * a47 * a57 * a65 + a16 * a23 * a34 * a47 * a57 * a65 + a16 * a24 * a32 * a47 * a57 * a65 + a16 * a24 * a34 * a47 * a57 * a65
den = wC1_1 + wC1_2 + wC1_3 + wC1_4 + wC1_5 + wC1_6 + wC1_7
v47 = a47 * C1_4 - a74 * C1_7
v42 = a42 * C1_4 - a24 * C1_2
v23 = a23 * C1_2 - a32 * C1_3
v61 = a61 * C1_1 - a16 * C1_6
eqs = [
wC1_1 ~ w1,
wC1_2 ~ w2,
wC1_3 ~ w3,
wC1_4 ~ w4,
wC1_5 ~ w5,
wC1_6 ~ w6,
wC1_7 ~ w7,
C1_1 ~ wC1_1 / den * ET_C1,
C1_2 ~ wC1_2 / den * ET_C1,
C1_3 ~ wC1_3 / den * ET_C1,
C1_4 ~ wC1_4 / den * ET_C1,
C1_7 ~ wC1_5 / den * ET_C1,
C1_5 ~ wC1_6 / den * ET_C1,
C1_6 ~ wC1_7 / den * ET_C1,
vQC1 ~ -0.5 * v47,
vROSC1 ~ v42,
vNADHC1 ~ -0.5 * v23,
vHresC1 ~ 2 * v61,
TNC1 ~ -vNADHC1 / ET_C1,
]
return System(eqs, t; name)
endc1_gauthier (generic function with 1 method)Markevich 2015
Markevich 2015 mass action law model.
https://pmc.ncbi.nlm.nih.gov/articles/PMC4426091/
The redox potential of N2 is adjusted to -150mV in B. taurus mitochondria instead of -80mV in E. coli(?).
function c1_markevich_full(; name=:c1markevich_full,
Q_n=1.8mM, QH2_n=0.2mM,
nad=500μM, nadh=500μM,
dpsi=150mV, O2=6μM, sox_m=0.01μM,
h_i=exp10(-7) * Molar, h_m=exp10(-7.6) * Molar,
DOX=0μM, ROTENONE_BLOCK=0)
@independent_variables t
D = Differential(t)
@parameters begin
Em_O2_SOX = -160mV ## O2/Superoxide redox potential
Em_FMN_FMNsq = -387mV ## FMN/FMNH- avg redox potential
Em_FMNsq_FMNH = -293mV ## FMN semiquinone/FMNH- redox potential
Em_FMN_FMNH = -340mV ## FMN/FMNH- avg redox potential
Em_NAD = -320mV ## NAD/NADH avg redox potential
Em_N3 = -250mV
Em_N2 = -150mV
Em_N1a = -370mV
Em_Q_SQ_C1 = -300mV ## -213mV in Markevich, 2015
Em_SQ_QH2_C1 = +500mV ## ~800mV (?) in Markevich, 2015
ET_C1 = 17μM ## Activity of complex I
# DOX IC50 on complex I
KI_DOX_C1 = 400μM
kf1_C1 = 83Hz / μM
KEQ1_C1 = 0.01 / μM
kr1_C1 = kf1_C1 / KEQ1_C1
kf3_C1 = 1e6Hz
KEQ3_C1 = 25μM
kr3_C1 = kf3_C1 / KEQ3_C1
kf2_C1 = 1.44e12Hz
KEQ2_C1 = exp(2iVT * (Em_FMN_FMNH - Em_NAD)) / KEQ1_C1 / KEQ3_C1
kr2_C1 = kf2_C1 / KEQ2_C1
kf4_C1 = 1Hz / μM
KEQ4_C1 = 0.001 / μM
kr4_C1 = kf4_C1 / KEQ4_C1
kf5_C1 = 2Hz / μM
KEQ5_C1 = 0.02 / μM
kr5_C1 = kf5_C1 / KEQ5_C1
kf6_C1 = 5e8Hz / μM
KEQ6_C1 = exp(iVT * (Em_N3 - Em_FMNsq_FMNH))
kr6_C1 = kf6_C1 / KEQ6_C1
kf7_C1 = 10000Hz / μM
KEQ7_C1 = exp(iVT * (Em_N2 - Em_N3))
kr7_C1 = kf7_C1 / KEQ7_C1
kf8_C1 = 10Hz / μM
KEQ8_C1 = 0.1 / μM ## Association constant for Q
kr8_C1 = kf8_C1 / KEQ8_C1
kf9_C1 = 4e5Hz / μM
KEQ9_C1 = exp(iVT * (Em_Q_SQ_C1 - Em_N2))
kr9_C1 = kf9_C1 / KEQ9_C1
kf10_C1 = 2e6Hz / μM
KEQ10_C1 = exp(iVT * (Em_N1a - Em_FMN_FMNsq))
KEQ10B_C1 = exp(iVT * (Em_FMNsq_FMNH - Em_N1a))
kr10_C1 = kf10_C1 / KEQ10_C1
kr10b_C1 = kf10_C1 / KEQ10B_C1
kf11_C1 = 1e9Hz / μM
KEQ11_C1 = exp(iVT * (Em_N3 - Em_FMN_FMNsq))
kr11_C1 = kf11_C1 / KEQ11_C1
kf13_C1 = 2.7e6Hz / μM
kf14_C1 = 1000Hz
KEQ14_C1 = 20μM ## Dissociation constant for QH2
kr14_C1 = kf14_C1 / KEQ14_C1
kf16_C1 = 2Hz / μM ## SOX production rate from If site
KEQ16_C1 = exp(iVT * (Em_O2_SOX - Em_FMNsq_FMNH))
kr16_C1 = kf16_C1 / KEQ16_C1
kf17_C1 = 0.04Hz / μM ## SOX production rate from Iq site
KEQ17_C1 = exp(iVT * (Em_O2_SOX - Em_Q_SQ_C1))
kr17_C1 = kf17_C1 / KEQ17_C1
end
@variables begin
Iq_C1(t) ## Conserved
Q_C1(t) = 0
SQ_C1(t) = 0
QH2_C1(t) = 0
FMN(t) ## Conserved
FMN_NADH(t) = 0
FMNH_NAD(t) = 0
FMN_NAD(t) = 0
FMNH_NADH(t) = 0
FMNH(t) = 0
FMNsq(t) = 0
N2_C1(t)
N2r_C1(t) = 0
N3_C1(t)
N3r_C1(t) = 0
N1a_C1(t)
N1ar_C1(t) = 0
KEQ13_C1(t)
vQC1(t)
vQH2C1(t)
vNADHC1(t)
vNADC1(t)
vROSIf(t)
vROSIq(t)
vROSC1(t)
TNC1(t) ## NADH turnover number
vHresC1(t)
end
fhm = h_m / 1E-7Molar
C1_INHIB = (1 - ROTENONE_BLOCK)
# NADH + FMN = FMN.NADH
v1 = kf1_C1 * nadh * FMN - kr1_C1 * FMN_NADH
# FMN.NADH = FMNH−.NAD+
v2 = kf2_C1 * FMN_NADH - kr2_C1 * FMNH_NAD
# FMNH−.NAD+ = FMNH− + NAD+
v3 = kf3_C1 * FMNH_NAD - kr3_C1 * FMNH * nad
# FMN + NAD+ = FMN.NAD+
v4 = kf4_C1 * nad * FMN - kr4_C1 * FMN_NAD
# FMNH− + NADH = FMNH−.NADH
v5 = kf5_C1 * FMNH * nadh - kr5_C1 * FMNH_NADH
# FMNH− + N3 = FMNHsq + N3−
v6 = kf6_C1 * FMNH * N3_C1 - kr6_C1 * FMNsq * N3r_C1
# N3− + N2 = N3 + N2−
v7 = kf7_C1 * N3r_C1 * N2_C1 - kr7_C1 * N3_C1 * N2r_C1
# Q association
q = Q_n * C1_INHIB
v8 = kf8_C1 * Iq_C1 * q - kr8_C1 * Q_C1
# CI.Q + N2− = CIQsq + N2
v9 = kf9_C1 * Q_C1 * N2r_C1 - kr9_C1 * SQ_C1 * N2_C1
# FMNHsq + N1a = FMN + N1a− + Hi+
v10 = kf10_C1 * FMNsq * N1a_C1 - kr10_C1 * FMN * N1ar_C1 * fhm
# FMNsq + N1a− = FMNH- + N1a
v10b = kf10_C1 * FMNsq * N1ar_C1 - kr10b_C1 * FMNH * N1a_C1
# FMNHsq + N3 = FMN + N3− + Hi+
v11 = kf11_C1 * FMNsq * N3_C1 - kr11_C1 * FMN * N3r_C1 * fhm
# N2 + N3− = N2− + N3
v12 = v7
# Second electron transfer
v13 = kf13_C1 * (SQ_C1 * N2r_C1 * fhm^2 - QH2_C1 * N2_C1 / KEQ13_C1)
# QH2 dissociation
qh2 = QH2_n * C1_INHIB
v14 = kf14_C1 * QH2_C1 - kr14_C1 * Iq_C1 * qh2
# Flavin site ROS generation
v16 = kf16_C1 * FMNH * O2 - kr16_C1 * FMNsq * sox_m
# Quinone site ROS generation
v17 = kf17_C1 * SQ_C1 * O2 - kr17_C1 * Q_C1 * sox_m
eqs = [
ET_C1 ~ N2r_C1 + N2_C1,
ET_C1 ~ N3r_C1 + N3_C1,
ET_C1 ~ N1ar_C1 + N1a_C1,
ET_C1 ~ Iq_C1 + Q_C1 + SQ_C1 + QH2_C1,
ET_C1 ~ FMN + FMN_NADH + FMNH_NAD + FMN_NAD + FMNH_NADH + FMNH + FMNsq,
KEQ13_C1 ~ exp(iVT * (Em_SQ_QH2_C1 - Em_N2 - 4dpsi)) * (h_m / h_i)^4,
D(FMN_NADH) ~ v1 - v2,
D(FMNH_NAD) ~ v2 - v3,
D(FMN_NAD) ~ v4,
D(FMNH_NADH) ~ v5,
D(FMNH) ~ v3 - v5 - v16 - v6 + v10b,
D(FMNsq) ~ v6 + v16 - v10 - v11 - v10b,
D(N1ar_C1) ~ v10 - v10b,
D(N3r_C1) ~ v6 + v11 - v7 - v12,
D(N2r_C1) ~ v7 + v12 - v9 - v13,
D(Q_C1) ~ v8 - v9 + v17,
D(SQ_C1) ~ v9 - v17 - v13,
D(QH2_C1) ~ v13 - v14,
# Positive: production; negative: consumption
vNADHC1 ~ -(v1 + v5),
vNADC1 ~ v3 - v4,
vQC1 ~ -v8,
vQH2C1 ~ v14,
vROSIf ~ v16,
vROSIq ~ v17,
vHresC1 ~ 4 * v13,
vROSC1 ~ vROSIf + vROSIq,
TNC1 ~ -vNADHC1 / ET_C1,
]
return System(eqs, t; name)
endc1_markevich_full (generic function with 1 method)Simplified Markevich
Simplified Markevich complex I model - Rapid equilibrium at the flavin site - QSSA for the catalytic cycle at the quinone site
function c1_markevich_s(; name=:c1s,
Q_n=1800μM, QH2_n=200μM,
nad=2500μM, nadh=500μM,
dpsi=150mV, O2=6μM, sox_m=0.01μM,
h_i=exp10(-7) * Molar, h_m=exp10(-7.6) * Molar,
DOX=0μM, ROTENONE_BLOCK=0, MT_PROT=1)
@independent_variables t
D = Differential(t)
@parameters begin
ET_C1 = 17μM ## Activity of complex I
KI_DOX_C1 = 400μM ## DOX IC50 on complex I
Em_O2_SOX = -160mV ## O2/Superoxide redox potential
Em_FMN_FMNsq = -387mV ## FMN/FMNH- avg redox potential
Em_FMNsq_FMNH = -293mV ## FMN semiquinone/FMNH- redox potential
Em_FMN_FMNH = -340mV ## FMN/FMNH- avg redox potential
Em_NAD = -320mV ## NAD/NADH avg redox potential
Em_N3 = -250mV
Em_N2 = -150mV
Em_Q_SQ_C1 = -300mV ## -213mV in Markevich, 2015
Em_SQ_QH2_C1 = +500mV ## ~800mV (?) in Markevich, 2015
KI_NADH_C1 = 50μM
KD_NADH_C1 = 100μM
KI_NAD_C1 = 1000μM
KD_NAD_C1 = 25μM
# NADH + FMN = NAD+ + FMNH-
KEQ_NADH_FMN = exp(2iVT * (Em_FMN_FMNH - Em_NAD))
# 2FMNsq = (N1a) = FMN + FMNH- + H+
rKEQ_FMNsq_Dis = exp(-iVT * (Em_FMNsq_FMNH - Em_FMN_FMNsq))
# FMNH- + N3 = FMNsq + N3-
KEQ_FMNH_N3 = exp(iVT * (Em_N3 - Em_FMNsq_FMNH))
# N3- + N2 = N3 + N2-
kf7_C1 = 10000Hz / μM
rKEQ7_C1 = exp(-iVT * (Em_N2 - Em_N3))
kb7_C1 = kf7_C1 * rKEQ7_C1
kf8_C1 = 10Hz / μM
rKEQ8_C1 = 10μM
kb8_C1 = kf8_C1 * rKEQ8_C1
kf9_C1 = 4E5Hz / μM
rKEQ9_C1 = exp(-iVT * (Em_Q_SQ_C1 - Em_N2))
kb9_C1 = kf9_C1 * rKEQ9_C1
kf13_C1 = 2.7e6Hz / μM
kf14_C1 = 1000Hz
rKEQ14_C1 = inv(20μM)
kb14_C1 = kf14_C1 * rKEQ14_C1
kf16_C1 = 2Hz / μM ## SOX production rate from If site
rKEQ16_C1 = exp(-iVT * (Em_O2_SOX - Em_FMNsq_FMNH))
kb16_C1 = kf16_C1 * rKEQ16_C1
kf17_C1 = 0.04Hz / μM ## SOX production rate from Iq site
rKEQ17_C1 = exp(-iVT * (Em_O2_SOX - Em_Q_SQ_C1))
kb17_C1 = kf17_C1 * rKEQ17_C1
end
@variables begin
# Flavin site
FMN(t)
FMN_NAD(t)
FMNsq(t)
FMNH(t)
FMNH_NADH(t)
FMN_NADH(t)
FMNH_NAD(t)
# FeS cluster
N3_C1(t)
N3r_C1(t)
N2_C1(t)
N2r_C1(t) = 0
# Quinone site
C1(t)
Q_C1(t)
SQ_C1(t)
QH2_C1(t)
rKEQ_N2r_SQ(t)
# Reaction rates
vQC1(t)
vQH2C1(t)
vROSC1(t)
vROSIf(t)
vROSIq(t)
vNADHC1(t)
vNADC1(t)
TNC1(t)
vHresC1(t)
end
C1_CONC = ET_C1 * MT_PROT
C1_INHIB = (1 - ROTENONE_BLOCK) / (1 + (DOX / KI_DOX_C1)^3)
# Mitochondrial pH factor
fhm = h_m * inv(1E-7Molar)
# Flavin site in rapid equilibrium
# Weights in the flavin site
wFMN = 1
wFMN_NAD = wFMN * nad / KI_NAD_C1
wFMN_NADH = wFMN * nadh / KD_NADH_C1
wFMNH = wFMN * (nadh / nad) * KEQ_NADH_FMN
wFMNH_NAD = wFMNH * nad / KD_NAD_C1
wFMNH_NADH = wFMNH * nadh / KI_NADH_C1
wFMNsq = NaNMath.sqrt(wFMN * wFMNH * rKEQ_FMNsq_Dis * fhm)
fDen = wFMN + wFMN_NAD + wFMNH + wFMNH_NADH + wFMNsq + wFMN_NADH + wFMNH_NAD
fC1 = C1_CONC / fDen
# Flavin site ROS generation
v16 = kf16_C1 * FMNH * O2 - kb16_C1 * FMNsq * sox_m
# N3− + N2 = N3 + N2−
v7 = kf7_C1 * N3r_C1 * N2_C1 - kb7_C1 * N3_C1 * N2r_C1
v12 = v7
# Quinone site state transition rates
# C1 + Q = Q_C1
b12 = kf8_C1 * Q_n * C1_INHIB
b21 = kb8_C1
v8 = b12 * C1 - b21 * Q_C1
# Q_C1 + N2r = SQ_C1 + N2
b23a = kf9_C1 * N2r_C1
b32a = kb9_C1 * N2_C1
v9 = b23a * Q_C1 - b32a * SQ_C1
# C1_SQ + N2r + 6Hm = C1_QH2 + N2 + 4Hi
b34 = kf13_C1 * N2r_C1 * fhm^2
b43 = kf13_C1 * rKEQ_N2r_SQ * N2_C1
v13 = b34 * SQ_C1 - b43 * QH2_C1
# C1_QH2 = C1 + QH2
b41 = kf14_C1
b14 = kb14_C1 * QH2_n * C1_INHIB
v14 = b41 * QH2_C1 - b14 * C1
# C1_SQ + O2 = C1_Q + sox
b32b = kf17_C1 * O2
b23b = kb17_C1 * sox_m
v17 = b32b * SQ_C1 - b23b * Q_C1
b23 = b23a + b23b
b32 = b32a + b32b
# KA pattern
wC1 = b21 * b32 * b41 + b21 * b32 * b43 + b21 * b34 * b41 + b23 * b34 * b41
wC1_Q = b12 * b32 * b41 + b12 * b32 * b43 + b12 * b34 * b41 + b14 * b32 * b43
wC1_SQ = b12 * b23 * b41 + b12 * b23 * b43 + b14 * b21 * b43 + b14 * b23 * b43
wC1_QH2 = b12 * b23 * b34 + b14 * b21 * b32 + b14 * b21 * b34 + b14 * b23 * b34
qDen = wC1 + wC1_Q + wC1_SQ + wC1_QH2
qC1 = C1_CONC / qDen
eqs = [
rKEQ_N2r_SQ ~ exp(-iVT * (Em_SQ_QH2_C1 - Em_N2 - 4dpsi)) * (h_i / h_m)^4,
FMN ~ wFMN * fC1,
FMN_NAD ~ wFMN_NAD * fC1,
FMNH ~ wFMNH * fC1,
FMNsq ~ wFMNsq * fC1,
FMNH_NADH ~ wFMNH_NADH * fC1,
FMN_NADH ~ wFMN_NADH * fC1,
FMNH_NAD ~ wFMNH_NAD * fC1,
N3_C1 ~ C1_CONC * FMNsq / (FMNsq + FMNH * KEQ_FMNH_N3),
C1_CONC ~ N3_C1 + N3r_C1,
C1_CONC ~ N2_C1 + N2r_C1,
D(N2r_C1) ~ v7 + v12 - v9 - v13,
C1 ~ wC1 * qC1,
Q_C1 ~ wC1_Q * qC1,
SQ_C1 ~ wC1_SQ * qC1,
QH2_C1 ~ wC1_QH2 * qC1,
vQC1 ~ -v8,
vNADHC1 ~ -0.5 * (v7 + v12 + v16),
vROSIf ~ v16,
vROSIq ~ v17,
vROSC1 ~ vROSIf + vROSIq,
vQH2C1 ~ v14,
vHresC1 ~ 4 * v13,
vNADC1 ~ -vNADHC1,
TNC1 ~ vNADC1 / C1_CONC,
]
return System(eqs, t; name)
endc1_markevich_s (generic function with 1 method)Quinone site
Quinone site complex I model, assuming N2 at equilibrium with the flavin site. Adapted from the simplified Markevich complex I model.
function c1_q(; name=:c1q,
Q_n=1800μM, QH2_n=200μM,
nad=2500μM, nadh=500μM,
dpsi=150mV, O2=6μM, sox_m=0.01μM,
h_i=exp10(-7) * Molar, h_m=exp10(-7.6) * Molar,
DOX=0μM, ROTENONE_BLOCK=0, MT_PROT=1)
@independent_variables t
D = Differential(t)
@parameters begin
ET_C1 = 17μM ## Activity of complex I
KI_DOX_C1 = 400μM ## DOX IC50 on complex I
Em_O2_SOX = -160mV ## O2/Superoxide redox potential
Em_FMN_FMNsq = -387mV ## FMN/FMNH- avg redox potential
Em_FMNsq_FMNH = -293mV ## FMN semiquinone/FMNH- redox potential
Em_FMN_FMNH = -340mV ## FMN/FMNH- avg redox potential
Em_NAD = -320mV ## NAD/NADH avg redox potential
Em_N3 = -250mV
Em_N2 = -150mV
Em_Q_SQ_C1 = -300mV ## -213mV in Markevich's model
Em_SQ_QH2_C1 = +500mV
KI_NADH_C1 = 50μM
KD_NADH_C1 = 100μM
KI_NAD_C1 = 1000μM
KD_NAD_C1 = 25μM
# NADH + FMN = NAD+ + FMNH-
KEQ_NADH_FMN = exp(2iVT * (Em_FMN_FMNH - Em_NAD))
# 2FMNsq = (ISC) = FMN + FMNH- + H+
rKEQ_FMNsq_Dis = exp(-iVT * (Em_FMNsq_FMNH - Em_FMN_FMNsq))
# FMNH- + N2 = FMNsq + N2-
KEQ_FMNH_N2 = exp(iVT * (Em_N2 - Em_FMNsq_FMNH))
# I + Q = IQ
kf8_C1 = 10Hz / μM
KEQ8_C1 = 0.1 / μM
kr8_C1 = kf8_C1 / KEQ8_C1
# Q + e- = Q-
kf9_C1 = 1e4Hz / μM ## 4e5Hz / μM
KEQ9_C1 = exp(iVT * (Em_Q_SQ_C1 - Em_N2))
kr9_C1 = kf9_C1 / KEQ9_C1
# Q- + e- + 6Hm = QH2 + 4Hi
kf13_C1 = 6e4Hz / μM ## 2.7e6Hz / μM
# C1_QH2 = C1 + QH2
kf14_C1 = 1000Hz
KEQ14_C1 = 20μM
kr14_C1 = kf14_C1 / KEQ14_C1 ## 50Hz / μM
kf16_C1 = 2Hz / μM ## SOX production rate from If site
KEQ16_C1 = exp(iVT * (Em_O2_SOX - Em_FMNsq_FMNH))
kr16_C1 = kf16_C1 / KEQ16_C1
kf17_C1 = 0.04Hz / μM ## SOX production rate from Iq site
KEQ17_C1 = exp(iVT * (Em_O2_SOX - Em_Q_SQ_C1))
kr17_C1 = kf17_C1 / KEQ17_C1
end
@variables begin
# Flavin site
FMN(t)
FMN_NAD(t)
FMNsq(t)
FMNH(t)
FMNH_NADH(t)
FMN_NADH(t)
FMNH_NAD(t)
N2_C1(t)
N2r_C1(t)
# Quinone site
I_C1(t) ## Conserved
Q_C1(t) = 0
SQ_C1(t) = 0
QH2_C1(t) = 0
rKEQ_N2r_SQ(t)
# Reaction rates
vQC1(t)
vQH2C1(t)
vROSC1(t)
vROSIf(t)
vROSIq(t)
vNADHC1(t)
vNADC1(t)
TNC1(t)
vHresC1(t)
end
C1_CONC = ET_C1 * MT_PROT
C1_INHIB = (1 - ROTENONE_BLOCK) / (1 + (DOX / KI_DOX_C1)^3)
fhm = h_m * inv(1E-7Molar) ## Mitochondrial pH factor
# Flavin site in rapid equilibrium
# Weights in the flavin site
wFMN = 1
wFMN_NAD = wFMN * nad / KI_NAD_C1
wFMN_NADH = wFMN * nadh / KD_NADH_C1
wFMNH = wFMN * (nadh / nad) * KEQ_NADH_FMN
wFMNH_NAD = wFMNH * nad / KD_NAD_C1
wFMNH_NADH = wFMNH * nadh / KI_NADH_C1
wFMNsq = NaNMath.sqrt(wFMN * wFMNH * rKEQ_FMNsq_Dis * fhm)
fDen = wFMN + wFMN_NAD + wFMNH + wFMNH_NADH + wFMNsq + wFMN_NADH + wFMNH_NAD
fC1 = C1_CONC / fDen
# Quinone site state transitions
# Q + C1 = Q_C1
q = Q_n * C1_INHIB
v8 = kf8_C1 * I_C1 * q - kr8_C1 * Q_C1
# Q_C1 + N2r = SQ_C1 + N2
v9 = kf9_C1 * Q_C1 * N2r_C1 - kr9_C1 * SQ_C1 * N2_C1
# SQ_C1 + N2r + 6Hm = QH2_C1 + N2 + 4Hi
v13 = kf13_C1 * (fhm^2 * N2r_C1 * SQ_C1 - rKEQ_N2r_SQ * N2_C1 * QH2_C1)
# QH2_C1 = QH2 + C1
qh2 = QH2_n * C1_INHIB
v14 = kf14_C1 * QH2_C1 - kr14_C1 * I_C1 * qh2
# Flavin site ROS production
v16 = kf16_C1 * FMNH * O2 - kr16_C1 * FMNsq * sox_m
# Quinone site ROS production
v17 = kf17_C1 * SQ_C1 * O2 - kr17_C1 * Q_C1 * sox_m
eqs = [
rKEQ_N2r_SQ ~ exp(-iVT * (Em_SQ_QH2_C1 - Em_N2 - 4dpsi)) * (h_i / h_m)^4,
FMN ~ wFMN * fC1,
FMN_NAD ~ wFMN_NAD * fC1,
FMNH ~ wFMNH * fC1,
FMNsq ~ wFMNsq * fC1,
FMNH_NADH ~ wFMNH_NADH * fC1,
FMN_NADH ~ wFMN_NADH * fC1,
FMNH_NAD ~ wFMNH_NAD * fC1,
N2_C1 ~ C1_CONC * FMNsq / (FMNsq + FMNH * KEQ_FMNH_N2),
C1_CONC ~ N2r_C1 + N2_C1,
C1_CONC ~ I_C1 + Q_C1 + SQ_C1 + QH2_C1,
D(Q_C1) ~ v8 - v9 + v17,
D(SQ_C1) ~ v9 - v13 - v17,
D(QH2_C1) ~ v13 - v14,
vNADHC1 ~ -0.5 * (v9 + v13 + v16),
vROSIf ~ v16,
vROSIq ~ v17,
vROSC1 ~ vROSIf + vROSIq,
vQH2C1 ~ v14,
vQC1 ~ -v8,
vHresC1 ~ 4 * v13,
vNADC1 ~ -vNADHC1,
TNC1 ~ vNADC1 / C1_CONC,
]
return System(eqs, t; name)
endc1_q (generic function with 1 method)Prepare problem
alg = DynamicSS(TRBDF2())
ealg = EnsembleThreads()SciMLBase.EnsembleThreads()@parameters begin
Q_n = 1.8mM
QH2_n = 0.2mM
nad = 2500μM
nadh = 500μM
dpsi = 150mV
sox_m = 0.01μM
end\[ \begin{equation} \left[ \begin{array}{c} \mathtt{Q\_n} \\ \mathtt{QH2\_n} \\ \mathtt{nad} \\ \mathtt{nadh} \\ \mathtt{dpsi} \\ \mathtt{sox\_m} \\ \end{array} \right] \end{equation} \]
# Helper function
extract(sim, k) = map(s -> s[k], sim)extract (generic function with 1 method)@time sys_q = c1_q(; Q_n, QH2_n, nad, nadh, dpsi, sox_m) |> mtkcompile 25.313789 seconds (45.71 M allocations: 2.224 GiB, 1.82% gc time, 99.73% compilation time: 61% of which was recompilation)\[ \begin{align} \frac{\mathrm{d} \mathtt{QH2\_C1}\left( t \right)}{\mathrm{d}t} &= - \mathtt{kf14\_C1} \mathtt{QH2\_C1}\left( t \right) + \mathtt{QH2\_n} \mathtt{kr14\_C1} \mathtt{I\_C1}\left( t \right) + \mathtt{kf13\_C1} \left( 0.063096 \mathtt{SQ\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) - \mathtt{QH2\_C1}\left( t \right) \mathtt{rKEQ\_N2r\_SQ}\left( t \right) \mathtt{N2\_C1}\left( t \right) \right) \\ \frac{\mathrm{d} \mathtt{SQ\_C1}\left( t \right)}{\mathrm{d}t} &= - 6 \mathtt{kf17\_C1} \mathtt{SQ\_C1}\left( t \right) + \mathtt{kf9\_C1} \mathtt{Q\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) + \mathtt{kr17\_C1} \mathtt{sox\_m} \mathtt{Q\_C1}\left( t \right) - \mathtt{kr9\_C1} \mathtt{SQ\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) - \mathtt{kf13\_C1} \left( 0.063096 \mathtt{SQ\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) - \mathtt{QH2\_C1}\left( t \right) \mathtt{rKEQ\_N2r\_SQ}\left( t \right) \mathtt{N2\_C1}\left( t \right) \right) \\ \frac{\mathrm{d} \mathtt{Q\_C1}\left( t \right)}{\mathrm{d}t} &= 6 \mathtt{kf17\_C1} \mathtt{SQ\_C1}\left( t \right) - \mathtt{kr8\_C1} \mathtt{Q\_C1}\left( t \right) + \mathtt{Q\_n} \mathtt{kf8\_C1} \mathtt{I\_C1}\left( t \right) - \mathtt{kf9\_C1} \mathtt{Q\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) - \mathtt{kr17\_C1} \mathtt{sox\_m} \mathtt{Q\_C1}\left( t \right) + \mathtt{kr9\_C1} \mathtt{SQ\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) \end{align} \]
@time prob_q = SteadyStateProblem(sys_q, [
sys_q.ET_C1 => 17μM,
sys_q.kf8_C1 => 5Hz / μM,
sys_q.kf9_C1 => 1000Hz / μM,
sys_q.kf13_C1 => 10000Hz / μM,
sys_q.kf16_C1 => 20Hz / μM,
sys_q.kf17_C1 => 0.4Hz / μM,
]) 15.168064 seconds (37.85 M allocations: 1.876 GiB, 1.34% gc time, 99.59% compilation time: 57% of which was recompilation)SteadyStateProblem with uType Vector{Float64}. In-place: true u0: 3-element Vector{Float64}: 0.0 0.0 0.0
@time sys_m = c1_markevich_full(; Q_n, QH2_n, nad, nadh, dpsi, sox_m) |> mtkcompile 1.563071 seconds (1.60 M allocations: 73.486 MiB, 1.14% gc time, 96.01% compilation time)\[ \begin{align} \frac{\mathrm{d} \mathtt{QH2\_C1}\left( t \right)}{\mathrm{d}t} &= - \mathtt{kf14\_C1} \mathtt{QH2\_C1}\left( t \right) + \mathtt{QH2\_n} \mathtt{kr14\_C1} \mathtt{Iq\_C1}\left( t \right) + \mathtt{kf13\_C1} \left( \frac{ - \mathtt{QH2\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right)}{\mathtt{KEQ13\_C1}\left( t \right)} + 0.063096 \mathtt{SQ\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) \right) \\ \frac{\mathrm{d} \mathtt{SQ\_C1}\left( t \right)}{\mathrm{d}t} &= - 6 \mathtt{kf17\_C1} \mathtt{SQ\_C1}\left( t \right) + \mathtt{kf13\_C1} \left( \frac{\mathtt{QH2\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right)}{\mathtt{KEQ13\_C1}\left( t \right)} - 0.063096 \mathtt{SQ\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) \right) + \mathtt{kf9\_C1} \mathtt{Q\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) + \mathtt{kr17\_C1} \mathtt{sox\_m} \mathtt{Q\_C1}\left( t \right) - \mathtt{kr9\_C1} \mathtt{SQ\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) \\ \frac{\mathrm{d} \mathtt{Q\_C1}\left( t \right)}{\mathrm{d}t} &= 6 \mathtt{kf17\_C1} \mathtt{SQ\_C1}\left( t \right) - \mathtt{kr8\_C1} \mathtt{Q\_C1}\left( t \right) + \mathtt{Q\_n} \mathtt{kf8\_C1} \mathtt{Iq\_C1}\left( t \right) - \mathtt{kf9\_C1} \mathtt{Q\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) - \mathtt{kr17\_C1} \mathtt{sox\_m} \mathtt{Q\_C1}\left( t \right) + \mathtt{kr9\_C1} \mathtt{SQ\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) \\ \frac{\mathrm{d} \mathtt{N2r\_C1}\left( t \right)}{\mathrm{d}t} &= \mathtt{kf13\_C1} \left( \frac{\mathtt{QH2\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right)}{\mathtt{KEQ13\_C1}\left( t \right)} - 0.063096 \mathtt{SQ\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) \right) + 2 \mathtt{kf7\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) - \mathtt{kf9\_C1} \mathtt{Q\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) - 2 \mathtt{kr7\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) + \mathtt{kr9\_C1} \mathtt{SQ\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) \\ \frac{\mathrm{d} \mathtt{N3r\_C1}\left( t \right)}{\mathrm{d}t} &= \mathtt{kf11\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) + \mathtt{kf6\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{FMNH}\left( t \right) - 2 \mathtt{kf7\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{N2\_C1}\left( t \right) - 0.25119 \mathtt{kr11\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{FMN}\left( t \right) - \mathtt{kr6\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) + 2 \mathtt{kr7\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{N2r\_C1}\left( t \right) \\ \frac{\mathrm{d} \mathtt{N1ar\_C1}\left( t \right)}{\mathrm{d}t} &= \mathtt{kf10\_C1} \mathtt{N1a\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) - \mathtt{kf10\_C1} \mathtt{N1ar\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) - 0.25119 \mathtt{kr10\_C1} \mathtt{N1ar\_C1}\left( t \right) \mathtt{FMN}\left( t \right) + \mathtt{kr10b\_C1} \mathtt{N1a\_C1}\left( t \right) \mathtt{FMNH}\left( t \right) \\ \frac{\mathrm{d} \mathtt{FMNsq}\left( t \right)}{\mathrm{d}t} &= 6 \mathtt{kf16\_C1} \mathtt{FMNH}\left( t \right) - \mathtt{kf10\_C1} \mathtt{N1a\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) - \mathtt{kf10\_C1} \mathtt{N1ar\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) - \mathtt{kf11\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) + \mathtt{kf6\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{FMNH}\left( t \right) + 0.25119 \mathtt{kr10\_C1} \mathtt{N1ar\_C1}\left( t \right) \mathtt{FMN}\left( t \right) + \mathtt{kr10b\_C1} \mathtt{N1a\_C1}\left( t \right) \mathtt{FMNH}\left( t \right) + 0.25119 \mathtt{kr11\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{FMN}\left( t \right) - \mathtt{kr16\_C1} \mathtt{sox\_m} \mathtt{FMNsq}\left( t \right) - \mathtt{kr6\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) \\ \frac{\mathrm{d} \mathtt{FMNH}\left( t \right)}{\mathrm{d}t} &= - 6 \mathtt{kf16\_C1} \mathtt{FMNH}\left( t \right) + \mathtt{kf3\_C1} \mathtt{FMNH\_NAD}\left( t \right) + \mathtt{kr5\_C1} \mathtt{FMNH\_NADH}\left( t \right) + \mathtt{kf10\_C1} \mathtt{N1ar\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) - \mathtt{kf5\_C1} \mathtt{nadh} \mathtt{FMNH}\left( t \right) - \mathtt{kf6\_C1} \mathtt{N3\_C1}\left( t \right) \mathtt{FMNH}\left( t \right) - \mathtt{kr10b\_C1} \mathtt{N1a\_C1}\left( t \right) \mathtt{FMNH}\left( t \right) + \mathtt{kr16\_C1} \mathtt{sox\_m} \mathtt{FMNsq}\left( t \right) - \mathtt{kr3\_C1} \mathtt{nad} \mathtt{FMNH}\left( t \right) + \mathtt{kr6\_C1} \mathtt{N3r\_C1}\left( t \right) \mathtt{FMNsq}\left( t \right) \\ \frac{\mathrm{d} \mathtt{FMNH\_NADH}\left( t \right)}{\mathrm{d}t} &= - \mathtt{kr5\_C1} \mathtt{FMNH\_NADH}\left( t \right) + \mathtt{kf5\_C1} \mathtt{nadh} \mathtt{FMNH}\left( t \right) \\ \frac{\mathrm{d} \mathtt{FMN\_NAD}\left( t \right)}{\mathrm{d}t} &= - \mathtt{kr4\_C1} \mathtt{FMN\_NAD}\left( t \right) + \mathtt{kf4\_C1} \mathtt{nad} \mathtt{FMN}\left( t \right) \\ \frac{\mathrm{d} \mathtt{FMNH\_NAD}\left( t \right)}{\mathrm{d}t} &= \mathtt{kf2\_C1} \mathtt{FMN\_NADH}\left( t \right) - \mathtt{kf3\_C1} \mathtt{FMNH\_NAD}\left( t \right) - \mathtt{kr2\_C1} \mathtt{FMNH\_NAD}\left( t \right) + \mathtt{kr3\_C1} \mathtt{nad} \mathtt{FMNH}\left( t \right) \\ \frac{\mathrm{d} \mathtt{FMN\_NADH}\left( t \right)}{\mathrm{d}t} &= - \mathtt{kf2\_C1} \mathtt{FMN\_NADH}\left( t \right) - \mathtt{kr1\_C1} \mathtt{FMN\_NADH}\left( t \right) + \mathtt{kr2\_C1} \mathtt{FMNH\_NAD}\left( t \right) + \mathtt{kf1\_C1} \mathtt{nadh} \mathtt{FMN}\left( t \right) \end{align} \]
prob_m = SteadyStateProblem(sys_m, [
sys_m.ET_C1 => 17μM,
sys_m.kf16_C1 => 20Hz / μM,
sys_m.kf17_C1 => 0.4Hz / μM,
])SteadyStateProblem with uType Vector{Float64}. In-place: true u0: 12-element Vector{Float64}: 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
@time sys_g = c1_gauthier(; Q_n, QH2_n, nad, nadh, dpsi, sox_m) |> mtkcompile 1.917932 seconds (3.10 M allocations: 144.503 MiB, 0.99% gc time, 97.03% compilation time)\[ \begin{align} \end{align} \]
# The parameter for ROS generation rate is adjusted (x10000) to be comparable to ROS generation from complex III
@time prob_g = SteadyStateProblem(sys_g, [
sys_g.K42_C1 => 6.0318Hz / mM * 10000
]) 1.921992 seconds (3.50 M allocations: 171.521 MiB, 0.97% gc time, 96.12% compilation time: 28% of which was recompilation)SteadyStateProblem with uType Nothing. In-place: true u0: nothing
Varying MMP
Simulations
dpsirange = 100mV:1mV:200mV
alter_dpsi = (prob, i, repeat) -> begin
prob.ps[dpsi] = dpsirange[i]
prob
end#7 (generic function with 1 method)@time mmp_q = solve(EnsembleProblem(prob_q; prob_func=alter_dpsi), alg, ealg; trajectories=length(dpsirange))
@time mmp_m = solve(EnsembleProblem(prob_m; prob_func=alter_dpsi), alg, ealg; trajectories=length(dpsirange))
@time mmp_g = solve(EnsembleProblem(prob_g; prob_func=alter_dpsi), alg, ealg; trajectories=length(dpsirange)) 6.483118 seconds (22.36 M allocations: 1.102 GiB, 6.24% gc time, 224.49% compilation time)
5.094021 seconds (18.10 M allocations: 966.798 MiB, 8.42% gc time, 219.13% compilation time)
0.954411 seconds (4.98 M allocations: 316.310 MiB, 10.50% gc time, 70.58% compilation time)EnsembleSolution Solution of length 101 with uType:
SciMLBase.NonlinearSolution{Float64, 1, Vector{Float64}, Nothing, SciMLBase.SteadyStateProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x318b15b0, 0x9acb9000, 0x7724fb87, 0x14b40c52, 0xd979d6f9), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x4edd3580, 0xd30cfe6a, 0x193db2ec, 0x2e4e47eb, 0x4cb7b38d), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x1a820b15, 0xad9a3ffc, 0x42485321, 0x863bd641, 0x12dfcee7), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{Any}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}}, Nothing, Nothing, Nothing, Nothing, Nothing}MMP vs NADH turnover
xs = dpsirange
ys = hcat(extract(mmp_g, sys_g.vNADHC1), extract(mmp_m, sys_m.vNADHC1), extract(mmp_q, sys_q.vNADHC1))
plot(xs, ys, xlabel="MMP (mV)", ylabel="NADH rate (mM/s)", label=["Gauthier" "Markevich" "Q site"])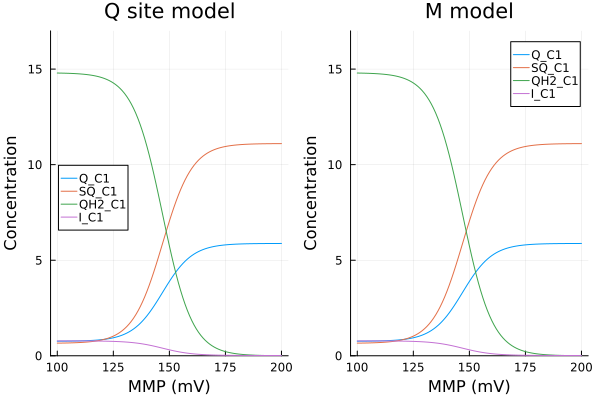
MMP vs Q site status
xs = dpsirange
ys = stack(extract.(Ref(mmp_q), [sys_q.Q_C1, sys_q.SQ_C1, sys_q.QH2_C1, sys_q.I_C1]), dims=2)
pl1 = plot(xs, ys, xlabel="MMP (mV)", ylabel="Concentration", label=["Q_C1" "SQ_C1" "QH2_C1" "I_C1"], title="Q site model", legend=:left, ylims=(0, 17μM))
ys2 = stack(extract.(Ref(mmp_m), [sys_m.Q_C1, sys_m.SQ_C1, sys_m.QH2_C1, sys_m.Iq_C1]), dims=2)
pl2 = plot(xs, ys, xlabel="MMP (mV)", ylabel="Concentration", label=["Q_C1" "SQ_C1" "QH2_C1" "I_C1"], title="M model", ylims=(0, 17μM))
plot(pl1, pl2)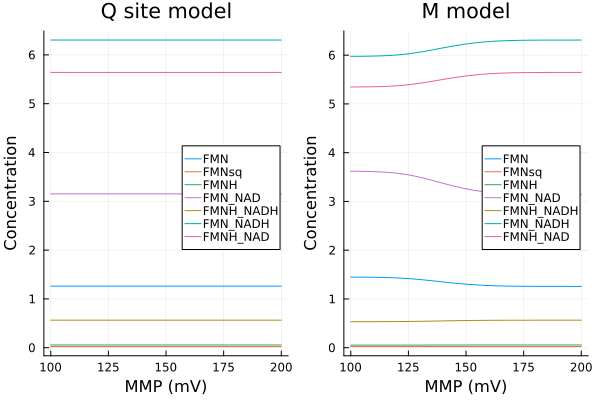
MMP vs Flavin site status
xs = dpsirange
ys = stack(extract.(Ref(mmp_q), [sys_q.FMN, sys_q.FMNsq, sys_q.FMNH, sys_q.FMN_NAD, sys_q.FMNH_NADH, sys_q.FMN_NADH, sys_q.FMNH_NAD]), dims=2)
pl1 = plot(xs, ys, xlabel="MMP (mV)", ylabel="Concentration", label=["FMN" "FMNsq" "FMNH" "FMN_NAD" "FMNH_NADH" "FMN_NADH" "FMNH_NAD"], title="Q site model", legend=:right)
ys = stack(extract.(Ref(mmp_m), [sys_m.FMN, sys_m.FMNsq, sys_m.FMNH, sys_m.FMN_NAD, sys_m.FMNH_NADH, sys_m.FMN_NADH, sys_m.FMNH_NAD]), dims=2)
pl2 = plot(xs, ys, xlabel="MMP (mV)", ylabel="Concentration", label=["FMN" "FMNsq" "FMNH" "FMN_NAD" "FMNH_NADH" "FMN_NADH" "FMNH_NAD"], title="M model", legend=:right)
plot(pl1, pl2)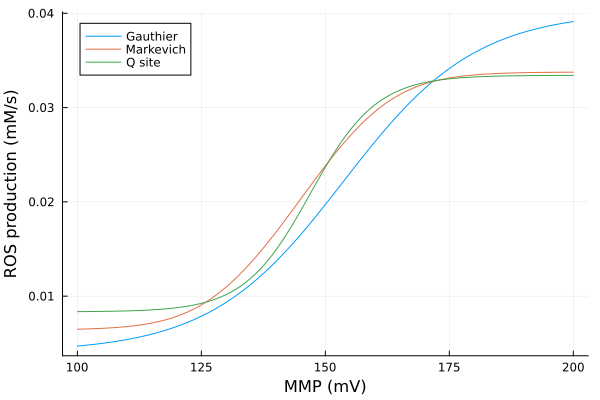
MMP vs ROS production
xs = dpsirange
ys_g = extract(mmp_g, sys_g.vROSC1)
ys_m = extract(mmp_m, sys_m.vROSC1)
ys_q = extract(mmp_q, sys_q.vROSC1)
plot(xs, [ys_g ys_m ys_q], xlabel="MMP (mV)", ylabel="ROS production (mM/s)", label=["Gauthier" "Markevich" "Q site"])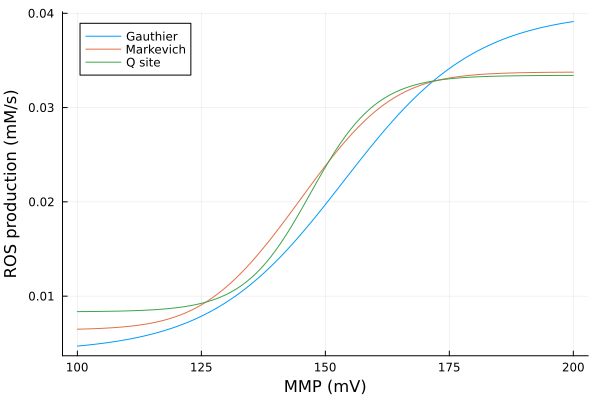
Varying NADH
Simulations
nadhrange = 10μM:10μM:2990μM
alter_nadh = (prob, i, repeat) -> begin
prob.ps[nadh] = nadhrange[i]
prob.ps[nad] = 3000μM - prob.ps[nadh]
prob
end#10 (generic function with 1 method)@time nad_q = solve(EnsembleProblem(prob_q; prob_func=alter_nadh), alg, ealg; trajectories=length(nadhrange))
@time nad_g = solve(EnsembleProblem(prob_g; prob_func=alter_nadh), alg, ealg; trajectories=length(nadhrange))
@time nad_m = solve(EnsembleProblem(prob_m; prob_func=alter_nadh), alg, ealg; trajectories=length(nadhrange)) 1.390332 seconds (6.83 M allocations: 359.466 MiB, 8.25% gc time, 79.59% compilation time)
2.132951 seconds (12.03 M allocations: 794.746 MiB, 27.95% gc time, 30.20% compilation time)
1.871119 seconds (10.15 M allocations: 687.206 MiB, 14.14% gc time, 31.82% compilation time)EnsembleSolution Solution of length 299 with uType:
Union{SciMLBase.NonlinearSolution{Float64, 1, Vector{Float64}, Vector{Float64}, SciMLBase.SteadyStateProblem{Vector{Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}}, SteadyStateDiffEq.DynamicSS{OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, Float64}, SciMLBase.ODESolution{Float64, 2, Vector{Vector{Float64}}, Nothing, Nothing, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, SciMLBase.ODEProblem{Vector{Float64}, Tuple{Float64, Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, true, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardODEProblem}, OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, OrdinaryDiffEqCore.InterpolationData{SciMLBase.ODEFunction{true, true, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Vector{Vector{Float64}}, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, cacheType, Nothing}, SciMLBase.DEStats, Nothing, Nothing, Nothing, Nothing}, Nothing, Nothing, Nothing} where cacheType<:(OrdinaryDiffEqSDIRK.TRBDF2Cache{Vector{Float64}, Vector{Float64}, Vector{Float64}, OrdinaryDiffEqSDIRK.TRBDF2Tableau{Float64, Float64}, N, typeof(OrdinaryDiffEqCore.trivial_limiter!)} where N<:(OrdinaryDiffEqNonlinearSolve.NLSolver{OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, true, Vector{Float64}, Float64, Nothing, Float64, OrdinaryDiffEqNonlinearSolve.NLNewtonCache{Vector{Float64}, Float64, Float64, Vector{Float64}, Matrix{Float64}, Matrix{Float64}, SciMLBase.UJacobianWrapper{true, SciMLBase.ODEFunction{true, true, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Float64, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}}, jcType, LinearSolve.LinearCache{Matrix{Float64}, Vector{Float64}, Vector{Float64}, SciMLBase.NullParameters, LinearSolve.DefaultLinearSolver, LinearSolve.DefaultLinearSolverInit{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Nothing, Nothing, Nothing, LinearAlgebra.SVD{Float64, Float64, Matrix{Float64}, Vector{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int32}}, Base.RefValue{Int32}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Base.RefValue{Int64}}, LinearAlgebra.QRPivoted{Float64, Matrix{Float64}, Vector{Float64}, Vector{Int64}}, Nothing, Nothing, Nothing, Nothing, Nothing}, LinearSolve.InvPreconditioner{LinearAlgebra.Diagonal{Float64, Vector{Float64}}}, LinearAlgebra.Diagonal{Float64, Vector{Float64}}, Float64, LinearSolve.LinearVerbosity{SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.CustomLevel, SciMLLogging.Silent, SciMLLogging.InfoLevel, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel}, Bool, LinearSolve.LinearSolveAdjoint{Missing}}}, Float64} where jcType<:Tuple{DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A), DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A)})), SciMLBase.NonlinearSolution{Float64, 1, Vector{Float64}, Vector{Float64}, SciMLBase.SteadyStateProblem{Vector{Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}}, SteadyStateDiffEq.DynamicSS{OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, Float64}, SciMLBase.ODESolution{Float64, 2, Vector{Vector{Float64}}, Nothing, Nothing, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, SciMLBase.ODEProblem{Vector{Float64}, Tuple{Float64, Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardODEProblem}, OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, OrdinaryDiffEqCore.InterpolationData{SciMLBase.ODEFunction{true, true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Vector{Vector{Float64}}, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, cacheType, Nothing}, SciMLBase.DEStats, Nothing, Nothing, Nothing, Nothing}, Nothing, Nothing, Nothing} where cacheType<:(OrdinaryDiffEqSDIRK.TRBDF2Cache{Vector{Float64}, Vector{Float64}, Vector{Float64}, OrdinaryDiffEqSDIRK.TRBDF2Tableau{Float64, Float64}, N, typeof(OrdinaryDiffEqCore.trivial_limiter!)} where N<:(OrdinaryDiffEqNonlinearSolve.NLSolver{OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, true, Vector{Float64}, Float64, Nothing, Float64, OrdinaryDiffEqNonlinearSolve.NLNewtonCache{Vector{Float64}, Float64, Float64, Vector{Float64}, Matrix{Float64}, Matrix{Float64}, SciMLBase.UJacobianWrapper{true, SciMLBase.ODEFunction{true, true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Float64, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}}, jcType, LinearSolve.LinearCache{Matrix{Float64}, Vector{Float64}, Vector{Float64}, SciMLBase.NullParameters, LinearSolve.DefaultLinearSolver, LinearSolve.DefaultLinearSolverInit{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Nothing, Nothing, Nothing, LinearAlgebra.SVD{Float64, Float64, Matrix{Float64}, Vector{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int32}}, Base.RefValue{Int32}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Base.RefValue{Int64}}, LinearAlgebra.QRPivoted{Float64, Matrix{Float64}, Vector{Float64}, Vector{Int64}}, Nothing, Nothing, Nothing, Nothing, Nothing}, LinearSolve.InvPreconditioner{LinearAlgebra.Diagonal{Float64, Vector{Float64}}}, LinearAlgebra.Diagonal{Float64, Vector{Float64}}, Float64, LinearSolve.LinearVerbosity{SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.CustomLevel, SciMLLogging.Silent, SciMLLogging.InfoLevel, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel}, Bool, LinearSolve.LinearSolveAdjoint{Missing}}}, Float64} where jcType<:Tuple{DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A), DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A)}))}NADH vs turnover
xs = nadhrange
ys_g = extract(nad_g, sys_g.vNADHC1)
ys_m = extract(nad_m, sys_m.vNADHC1)
ys_q = extract(nad_q, sys_q.vNADHC1)
plot(xs, [ys_g ys_m ys_q], xlabel="NADH (μM)", ylabel="NADH rate (mM/s)", label=["Gauthier" "Markevich" "Q site"])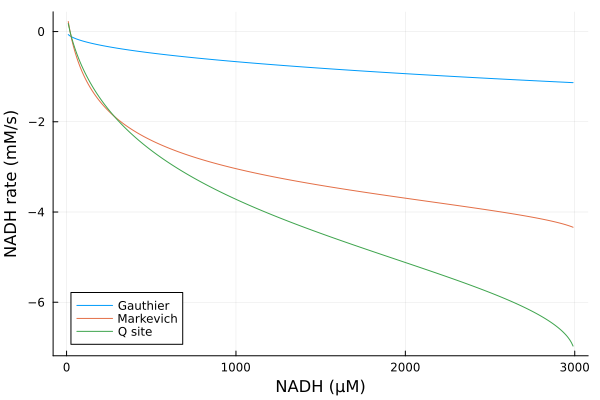
xs = nadhrange
ys = [extract(nad_m, sys_m.N2r_C1) extract(nad_q, sys_q.N2r_C1)] ./ μM
plot(xs, ys, xlabel="NADH (μM)", ylabel="Reduced N2 (μM)", label=["Markevich" "Q site"])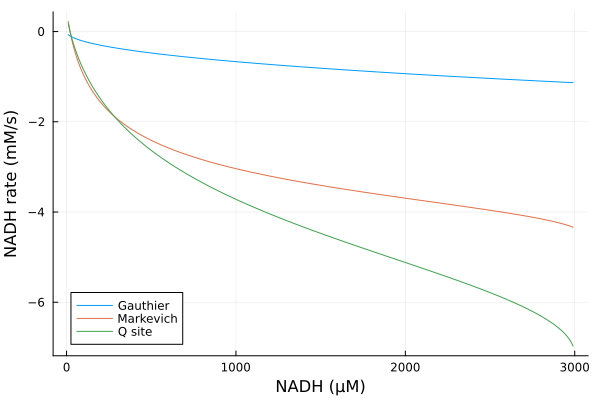
NADH vs ROS production
xs = nadhrange
ys = [extract(nad_g, sys_g.vROSC1) extract(nad_m, sys_m.vROSC1) extract(nad_q, sys_q.vROSC1)]
plot(xs, ys, xlabel="NADH (μM)", ylabel="ROS production (mM/s)", label=["Gauthier" "Markevich" "Q site"])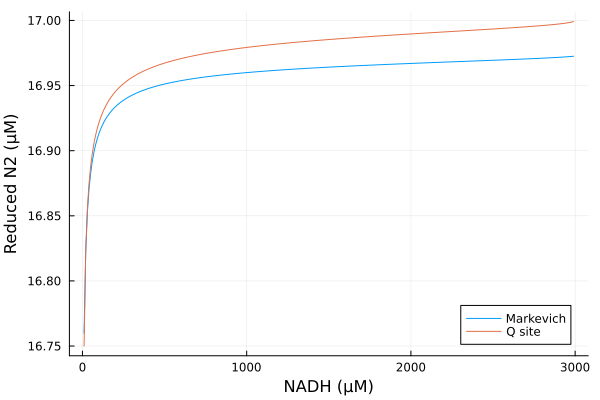
xs = nadhrange
ys = stack(extract.(Ref(nad_q), [sys_q.Q_C1, sys_q.SQ_C1, sys_q.QH2_C1, sys_q.I_C1]), dims=2)
pl1 = plot(xs, ys, xlabel="NADH (μM)", ylabel="Concentration (μM)", label=["Q_C1" "SQ_C1" "QH2_C1" "I_C1"], title="Q site", legend=:top, ylims=(0, 17))
ys = stack(extract.(Ref(nad_m), [sys_m.Q_C1, sys_m.SQ_C1, sys_m.QH2_C1, sys_m.Iq_C1]), dims=2)
pl2 = plot(xs, ys, xlabel="NADH (μM)", ylabel="Concentration", label=["Q_C1" "SQ_C1" "QH2_C1" "I_C1"], title="M model", ylims=(0, 17))
plot(pl1, pl2)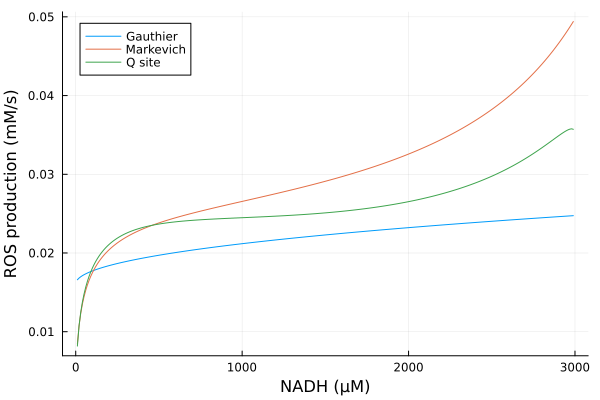
Varying Q/QH2
Simulations
qh2range = 10μM:10μM:1990μM
alter_qh2 = (prob, i, repeat) -> begin
prob.ps[QH2_n] = qh2range[i]
prob.ps[Q_n] = 2000μM - prob.ps[QH2_n]
prob
end#13 (generic function with 1 method)@time qh2_q = solve(EnsembleProblem(prob_q; prob_func=alter_qh2), alg, ealg; trajectories=length(qh2range))
@time qh2_g = solve(EnsembleProblem(prob_g; prob_func=alter_qh2), alg, ealg; trajectories=length(qh2range))
@time qh2_m = solve(EnsembleProblem(prob_m; prob_func=alter_qh2), alg, ealg; trajectories=length(qh2range)) 0.871144 seconds (4.48 M allocations: 236.159 MiB, 5.39% gc time, 42.89% compilation time)
1.237890 seconds (8.08 M allocations: 532.236 MiB, 11.84% gc time, 32.80% compilation time)
1.304382 seconds (6.85 M allocations: 471.530 MiB, 12.99% gc time, 29.12% compilation time)EnsembleSolution Solution of length 199 with uType:
Union{SciMLBase.NonlinearSolution{Float64, 1, Vector{Float64}, Vector{Float64}, SciMLBase.SteadyStateProblem{Vector{Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}}, SteadyStateDiffEq.DynamicSS{OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, Float64}, SciMLBase.ODESolution{Float64, 2, Vector{Vector{Float64}}, Nothing, Nothing, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, SciMLBase.ODEProblem{Vector{Float64}, Tuple{Float64, Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, true, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardODEProblem}, OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, OrdinaryDiffEqCore.InterpolationData{SciMLBase.ODEFunction{true, true, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Vector{Vector{Float64}}, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, cacheType, Nothing}, SciMLBase.DEStats, Nothing, Nothing, Nothing, Nothing}, Nothing, Nothing, Nothing} where cacheType<:(OrdinaryDiffEqSDIRK.TRBDF2Cache{Vector{Float64}, Vector{Float64}, Vector{Float64}, OrdinaryDiffEqSDIRK.TRBDF2Tableau{Float64, Float64}, N, typeof(OrdinaryDiffEqCore.trivial_limiter!)} where N<:(OrdinaryDiffEqNonlinearSolve.NLSolver{OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, true, Vector{Float64}, Float64, Nothing, Float64, OrdinaryDiffEqNonlinearSolve.NLNewtonCache{Vector{Float64}, Float64, Float64, Vector{Float64}, Matrix{Float64}, Matrix{Float64}, SciMLBase.UJacobianWrapper{true, SciMLBase.ODEFunction{true, true, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Float64, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}}, jcType, LinearSolve.LinearCache{Matrix{Float64}, Vector{Float64}, Vector{Float64}, SciMLBase.NullParameters, LinearSolve.DefaultLinearSolver, LinearSolve.DefaultLinearSolverInit{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Nothing, Nothing, Nothing, LinearAlgebra.SVD{Float64, Float64, Matrix{Float64}, Vector{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int32}}, Base.RefValue{Int32}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Base.RefValue{Int64}}, LinearAlgebra.QRPivoted{Float64, Matrix{Float64}, Vector{Float64}, Vector{Int64}}, Nothing, Nothing, Nothing, Nothing, Nothing}, LinearSolve.InvPreconditioner{LinearAlgebra.Diagonal{Float64, Vector{Float64}}}, LinearAlgebra.Diagonal{Float64, Vector{Float64}}, Float64, LinearSolve.LinearVerbosity{SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.CustomLevel, SciMLLogging.Silent, SciMLLogging.InfoLevel, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel}, Bool, LinearSolve.LinearSolveAdjoint{Missing}}}, Float64} where jcType<:Tuple{DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A), DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A)})), SciMLBase.NonlinearSolution{Float64, 1, Vector{Float64}, Vector{Float64}, SciMLBase.SteadyStateProblem{Vector{Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}}, SteadyStateDiffEq.DynamicSS{OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, Float64}, SciMLBase.ODESolution{Float64, 2, Vector{Vector{Float64}}, Nothing, Nothing, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, SciMLBase.ODEProblem{Vector{Float64}, Tuple{Float64, Float64}, true, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.ODEFunction{true, true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardODEProblem}, OrdinaryDiffEqSDIRK.TRBDF2{0, ADTypes.AutoForwardDiff{nothing, ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}}, Nothing, OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, typeof(OrdinaryDiffEqCore.DEFAULT_PRECS), Val{:forward}(), true, nothing, typeof(OrdinaryDiffEqCore.trivial_limiter!)}, OrdinaryDiffEqCore.InterpolationData{SciMLBase.ODEFunction{true, true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Vector{Vector{Float64}}, Vector{Float64}, Vector{Vector{Vector{Float64}}}, Nothing, cacheType, Nothing}, SciMLBase.DEStats, Nothing, Nothing, Nothing, Nothing}, Nothing, Nothing, Nothing} where cacheType<:(OrdinaryDiffEqSDIRK.TRBDF2Cache{Vector{Float64}, Vector{Float64}, Vector{Float64}, OrdinaryDiffEqSDIRK.TRBDF2Tableau{Float64, Float64}, N, typeof(OrdinaryDiffEqCore.trivial_limiter!)} where N<:(OrdinaryDiffEqNonlinearSolve.NLSolver{OrdinaryDiffEqNonlinearSolve.NLNewton{Rational{Int64}, Rational{Int64}, Rational{Int64}, Nothing}, true, Vector{Float64}, Float64, Nothing, Float64, OrdinaryDiffEqNonlinearSolve.NLNewtonCache{Vector{Float64}, Float64, Float64, Vector{Float64}, Matrix{Float64}, Matrix{Float64}, SciMLBase.UJacobianWrapper{true, SciMLBase.ODEFunction{true, true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xfb0c7da8, 0x031aa58b, 0xb72182c7, 0x57a3cbba, 0x480185b4), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0xedda6ce5, 0xc64fd0f8, 0x04789f25, 0x25fdc2d1, 0xf176123f), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, SciMLBase.OverrideInitData{SciMLBase.NonlinearProblem{Nothing, true, ModelingToolkit.MTKParameters{Vector{Float64}, StaticArraysCore.SVector{0, Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}, SciMLBase.NonlinearFunction{true, SciMLBase.FullSpecialize, ModelingToolkit.GeneratedFunctionWrapper{(2, 2, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9e75ff5c, 0x569e6946, 0xdf99c4d0, 0x991dfbdf, 0xc9726560), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2d711344, 0x7a9ccb96, 0xfcb0d583, 0x804a5d5b, 0x2c777abf), Nothing}}, LinearAlgebra.UniformScaling{Bool}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, ModelingToolkit.ObservedFunctionCache{ModelingToolkit.System}, Nothing, ModelingToolkit.System, Nothing, Nothing}, Base.Pairs{Symbol, Union{}, Nothing, @NamedTuple{}}, SciMLBase.StandardNonlinearProblem, Nothing, Nothing}, Nothing, Nothing, Nothing, ModelingToolkit.InitializationMetadata{ModelingToolkit.ReconstructInitializeprob{ModelingToolkit.var"#_getter#973"{Tuple{ComposedFunction{ModelingToolkit.PConstructorApplicator{typeof(identity)}, ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x96515b92, 0x3b729c5c, 0xb12c5daa, 0xf7ecaf16, 0xd816b330), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x2b42e12c, 0x6d835ddc, 0xc87748f5, 0x95b8db00, 0x7b2cf946), Nothing}}}}, Returns{StaticArraysCore.SVector{0, Float64}}, Returns{Tuple{}}, Returns{Tuple{}}, Returns{Tuple{}}}}, ComposedFunction{typeof(identity), ModelingToolkit.ObservedWrapper{true, ModelingToolkit.GeneratedFunctionWrapper{(2, 3, true), RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x9da934f5, 0xde419185, 0x1c689c96, 0xdb85219a, 0xd2ebbc7c), Nothing}, RuntimeGeneratedFunctions.RuntimeGeneratedFunction{(:ˍ₋out, :__mtk_arg_1, :___mtkparameters___, :t), ModelingToolkit.var"#_RGF_ModTag", ModelingToolkit.var"#_RGF_ModTag", (0x0466ff4b, 0x18eddd04, 0x44549885, 0xd768fa8d, 0x13589431), Nothing}}}}}, Nothing, ModelingToolkit.SetInitialUnknowns{SymbolicIndexingInterface.MultipleSetters{Vector{SymbolicIndexingInterface.ParameterHookWrapper{SymbolicIndexingInterface.SetParameterIndex{ModelingToolkit.ParameterIndex{SciMLStructures.Initials, Int64}}, SymbolicUtils.BasicSymbolic{Real}}}}}}, Val{true}}, Nothing}, Float64, ModelingToolkit.MTKParameters{Vector{Float64}, Vector{Float64}, Tuple{}, Tuple{}, Tuple{}, Tuple{}}}, jcType, LinearSolve.LinearCache{Matrix{Float64}, Vector{Float64}, Vector{Float64}, SciMLBase.NullParameters, LinearSolve.DefaultLinearSolver, LinearSolve.DefaultLinearSolverInit{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, LinearAlgebra.QRCompactWY{Float64, Matrix{Float64}, Matrix{Float64}}, Nothing, Nothing, Nothing, Nothing, Nothing, Nothing, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Vector{Int64}}, Nothing, Nothing, Nothing, LinearAlgebra.SVD{Float64, Float64, Matrix{Float64}, Vector{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int32}}, Base.RefValue{Int32}}, Tuple{LinearAlgebra.LU{Float64, Matrix{Float64}, Vector{Int64}}, Base.RefValue{Int64}}, LinearAlgebra.QRPivoted{Float64, Matrix{Float64}, Vector{Float64}, Vector{Int64}}, Nothing, Nothing, Nothing, Nothing, Nothing}, LinearSolve.InvPreconditioner{LinearAlgebra.Diagonal{Float64, Vector{Float64}}}, LinearAlgebra.Diagonal{Float64, Vector{Float64}}, Float64, LinearSolve.LinearVerbosity{SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.CustomLevel, SciMLLogging.Silent, SciMLLogging.InfoLevel, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.Silent, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel, SciMLLogging.WarnLevel}, Bool, LinearSolve.LinearSolveAdjoint{Missing}}}, Float64} where jcType<:Tuple{DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A), DifferentiationInterfaceForwardDiffExt.ForwardDiffTwoArgJacobianPrep{Nothing, C, Tuple{}} where C<:(ForwardDiff.JacobianConfig{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A, <:Tuple{Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A, Array{ForwardDiff.Dual{ForwardDiff.Tag{DiffEqBase.OrdinaryDiffEqTag, Float64}, Float64, _A}, 1} where _A}} where _A)}))}QH2 vs turnover
xs = qh2range
ys = [extract(qh2_g, sys_g.vNADHC1) extract(qh2_m, sys_m.vNADHC1) extract(qh2_q, sys_q.vNADHC1)]
plot(xs, ys, xlabel="QH2 (μM)", ylabel="NADH rate (mM/s)", label=["Gauthier" "Markevich" "Q site"])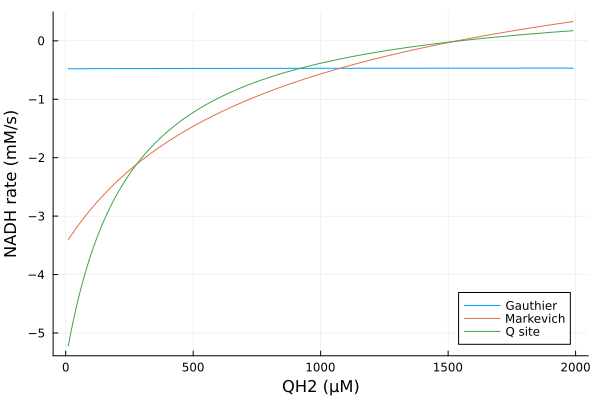
QH2 vs ROS production
xs = qh2range
ys = [extract(qh2_g, sys_g.vROSC1) extract(qh2_m, sys_m.vROSC1) extract(qh2_q, sys_q.vROSC1)]
plot(xs, ys, xlabel="QH2 (μM)", ylabel="ROS production", label=["Gauthier" "Markevich" "Q site"])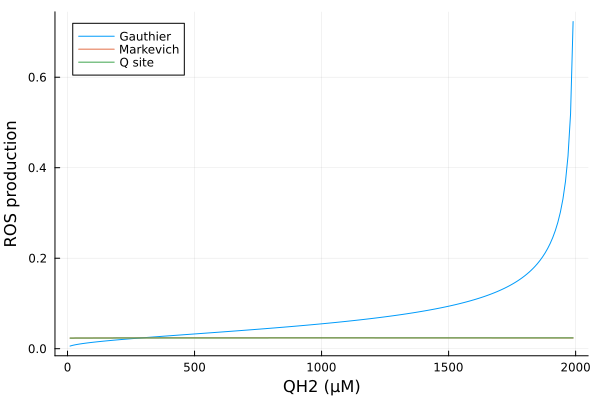
xs = qh2range
ys = stack(extract.(Ref(qh2_q), [sys_q.Q_C1, sys_q.SQ_C1, sys_q.QH2_C1, sys_q.I_C1]), dims=2)
pl1 = plot(xs, ys, xlabel="QH2 (μM)", ylabel="Concentration", label=["Q_C1" "SQ_C1" "QH2_C1" "I_C1"], title="Q site", legend=:top, ylims=(0, 17))
ys = stack(extract.(Ref(qh2_m), [sys_m.Q_C1, sys_m.SQ_C1, sys_m.QH2_C1, sys_m.Iq_C1]), dims=2)
pl2 = plot(xs, ys, xlabel="QH2 (μM)", ylabel="Concentration", label=["Q_C1" "SQ_C1" "QH2_C1" "I_C1"], title="Markevich", legend=:top, ylims=(0, 17))
plot(pl1, pl2)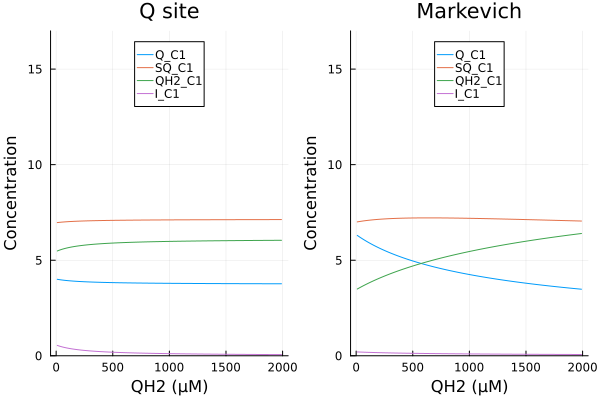
Gauthier model is sensitive to high QH2 because of slow NAD binding (k43).
@unpack C1_1, C1_3, C1_4, C1_5, C1_6, C1_7 = sys_g
xs = qh2range
ys = stack(extract.(Ref(qh2_g), [C1_3, C1_4]), dims=2) .* 1000
plot(xs, ys, xlabel="QH2 (μM)", ylabel="Conc (μM)", label=["C1_3" "C1_4"], lw=1.5)
This notebook was generated using Literate.jl.