using OrdinaryDiffEq
using ModelingToolkit
using ECMEDox
using ECMEDox: second, mM, Hz, μM, mV
using PlotsInitial conditions
1Hz pacing for 1000 seconds.
tend = 1000.0second
bcl = 1.0second
@named sys = build_model()
u0 = build_u0(sys)
sts = unknowns(sys)
alg = KenCarp47()
@unpack iStim = sys
callback = build_stim_callbacks(iStim, tend; period=bcl)
prob = ODEProblem(sys, u0, tend)ODEProblem with uType Vector{Float64} and tType Float64. In-place: true Initialization status: FULLY_DETERMINED Non-trivial mass matrix: false timespan: (0.0, 1.0e6) u0: 64-element Vector{Float64}: 2.196435053752864 0.0007273589705197244 0.000981691808598968 245.22202099807583 281.0719264404058 197.06621753790645 34.41477140951692 60.37913837798986 229.2919970960533 22.321405235243013 ⋮ 23.148552252520883 0.6928662120941113 0.20648605639609985 1295.5364065086924 1299.7940884726063 0.20381438659933854 145551.11317854663 10276.480036234318 -85.29107641956527
@time sol = solve(prob, alg; callback = callback, saveat=0.01second); 22.914749 seconds (21.44 M allocations: 4.336 GiB, 2.94% gc time, 35.25% compilation time)for i in sts
istr = replace(string(i), "(t)" => "")
println("sys.", istr, " => ", sol[i][end], ",")
endsys.gssg_i => 0.6265895252222011,
sys.h2o2_i => 0.00021599097781071342,
sys.sox_i => 0.00028190801934549915,
sys.cytc_ox => 190.9942064652317,
sys.cytc1_ox => 243.39572775573265,
sys.fes_ox => 138.12470541092236,
sys.blo_bhr => 25.6934437385322,
sys.blr_bho => 67.38162764988788,
sys.blo_bho => 231.22754320807363,
sys.QH2_p => 0.5303653651607938,
sys.QH2_n => 0.5680839234747104,
sys.Q_n => 1972.1657215559524,
sys.SQn => 54.11043560928229,
sys.SQp => 0.42196349549109147,
sys.N2r_C1 => 16.962747649718416,
sys.oaa => 0.003456587010348656,
sys.mal => 17.45908681538521,
sys.fum => 30.281799654800974,
sys.suc => 0.7824407723686897,
sys.scoa => 70.2733684372583,
sys.akg => 0.48375017081361893,
sys.isoc => 808.1399060776027,
sys.j_na => 0.9785809587362959,
sys.h_na => 0.9700517570637683,
sys.m_na => 0.0014537117796985393,
sys.x_k => 0.002826199931503989,
sys.htr_ca => 137.6817945837704,
sys.ltr_ca => 23.56607075064662,
sys.x_n1 => 0.0205160292613334,
sys.x_p3 => 0.010595307782848938,
sys.x_p2 => 0.012142111983837824,
sys.x_p1 => 0.0064703028622723315,
sys.x_p0 => 0.007276352366645881,
sys.crp_ic => 16676.918901741898,
sys.crp_i => 16746.777783498474,
sys.adp_ic => 37.750977045233356,
sys.x_yca => 0.7245465013652761,
sys.cca4_lcc => 9.809958117691816e-23,
sys.cca3_lcc => 3.1200393814447665e-17,
sys.cca2_lcc => 3.721593607559369e-12,
sys.cca1_lcc => 1.9730128695027383e-7,
sys.cca0_lcc => 0.0039225604278334564,
sys.o_lcc => 1.861547200225307e-23,
sys.c4_lcc => 9.736211892019993e-23,
sys.c3_lcc => 1.2377646320667778e-16,
sys.c2_lcc => 5.906074175051876e-11,
sys.c1_lcc => 1.2524994845846755e-5,
sys.pc2_ryr => 0.1268315869673352,
sys.po2_ryr => 2.8085358346271207e-9,
sys.po1_ryr => 0.00017254605527284203,
sys.O2 => 5.92015151055995,
sys.sox_m => 0.11424499555119991,
sys.dpsi => 171.47400536774467,
sys.nadh_m => 440.9173150522303,
sys.adp_m => 6.225787882099771,
sys.adp_i => 37.12263459703367,
sys.ca_m => 0.8518010873563447,
sys.ca_ss => 0.19792262061125476,
sys.ca_jsr => 1238.3749208775625,
sys.ca_nsr => 1242.3665362884317,
sys.ca_i => 0.19518567290704092,
sys.k_i => 144972.0873551958,
sys.na_i => 10213.43781732787,
sys.vm => -85.36718765864255,Action potential
plot(sol, idxs=sys.vm, legend=:right, tspan=(900second, 901second))
Citric acid cycle metabolites
Citrate and isocitrate have the highest concentrations.
@unpack cit, isoc, oaa, akg, scoa, suc, fum, mal = sys
plot(sol, idxs=[cit, isoc, oaa, akg, scoa, suc, fum, mal], legend=:right, title="CAC metabolites")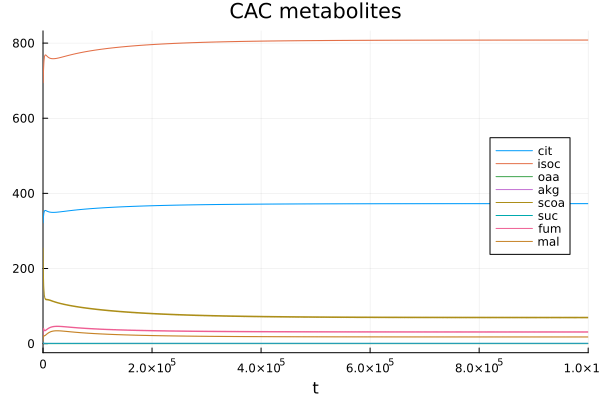
CAC flux
@unpack vMDH, vAAT, vIDH = sys
plot(sol, idxs=[vMDH, vAAT, vIDH], legend=:right, title="CAC flux")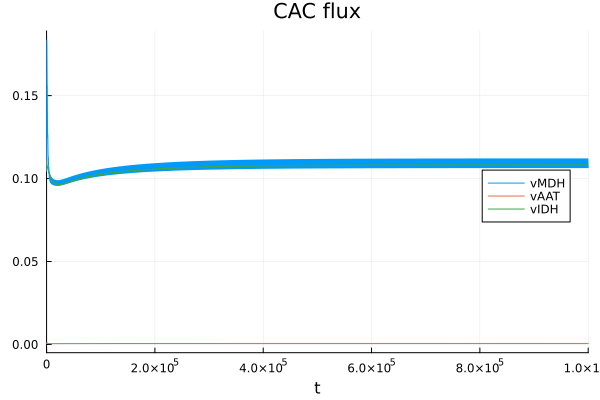
Q cycle
@unpack Q_n, SQn, QH2_n, QH2_p, Q_p, SQp, fes_ox, fes_rd, cytc_ox, cytc_rd = sys
plot(sol, idxs=[Q_n + Q_p, SQn, QH2_n + QH2_p, SQp], title="Q cycle", legend=:left, xlabel="Time (ms)", ylabel="Conc. (μM)")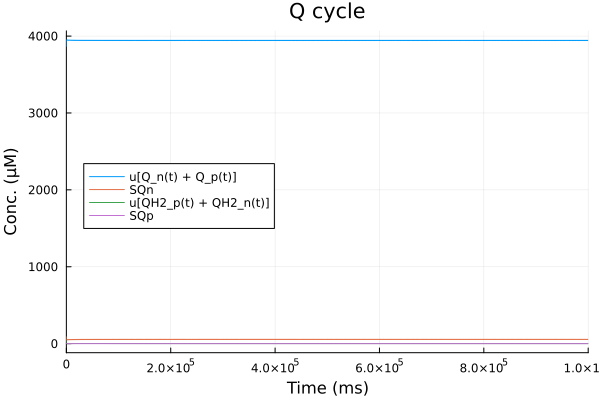
plot(sol, idxs=[fes_ox, fes_rd, cytc_ox, cytc_rd], title="Q cycle (downstream)", legend=:left, xlabel="Time (ms)", ylabel="Conc. (μM)")
Proton pumping
plot(sol, idxs = [sys.vHresC1, sys.vHresC3, sys.vHresC4], ylims=(0, 3))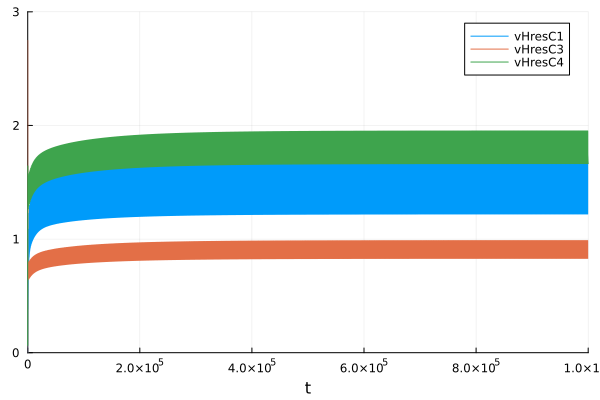
ROS
plot(sol, idxs = [sys.sox_i, sys.sox_m], tspan=(900e3, 910e3))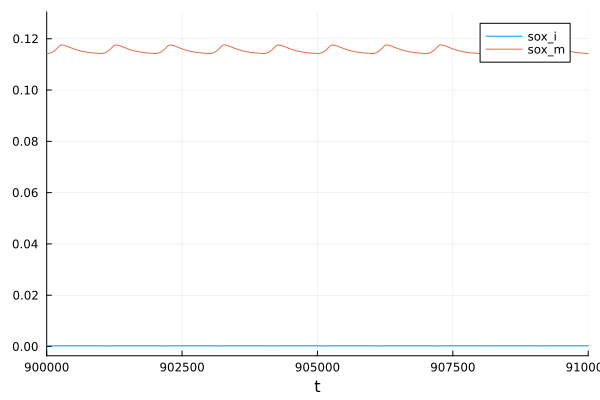
plot(sol, idxs = [sys.vROSIf, sys.vROSIq, sys.vROSC1, sys.vROSC3], tspan=(900e3, 910e3))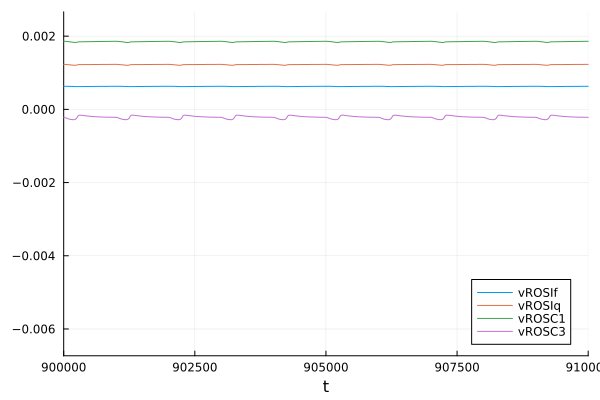
plot(sol, idxs=100 * sys.vROS / (sys.vO2 + sys.vROS), title="O2 Shunt", tspan=(900e3, 910e3), ylims=(0, 5))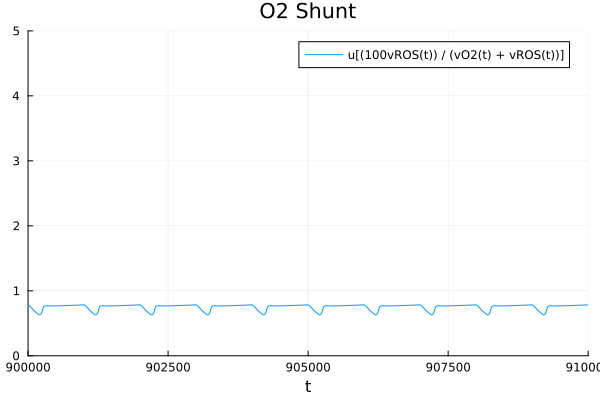
MMP
plot(sol, idxs = [sys.dpsi], tspan=(900e3, 910e3))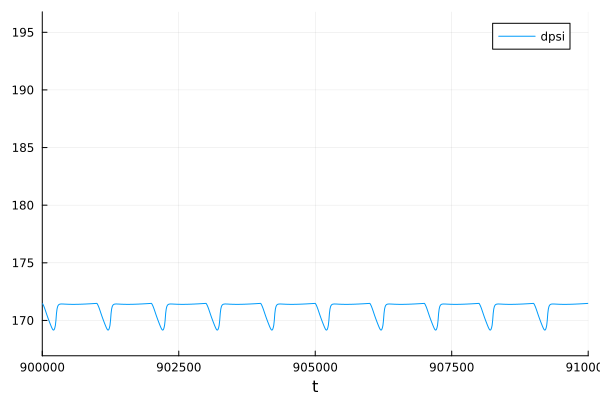
plot(sol, idxs = [sys.vC5], tspan=(900e3, 910e3))
Runtime information
using InteractiveUtils
InteractiveUtils.versioninfo()Julia Version 1.12.4
Commit 01a2eadb047 (2026-01-06 16:56 UTC)
Build Info:
Official https://julialang.org release
Platform Info:
OS: Linux (x86_64-linux-gnu)
CPU: 4 × AMD EPYC 7763 64-Core Processor
WORD_SIZE: 64
LLVM: libLLVM-18.1.7 (ORCJIT, znver3)
GC: Built with stock GC
Threads: 4 default, 1 interactive, 4 GC (on 4 virtual cores)
Environment:
JULIA_CPU_TARGET = generic;icelake-server,clone_all;znver3,clone_all
JULIA_CONDAPKG_OFFLINE = true
JULIA_CONDAPKG_BACKEND = Null
JULIA_CI = true
LD_LIBRARY_PATH = /opt/hostedtoolcache/Python/3.14.2/x64/lib
JULIA_NUM_THREADS = autousing Pkg
Pkg.status()Project ECMEDox v0.4.0
Status `~/work/ecme-rirr-dox/ecme-rirr-dox/Project.toml`
[459566f4] DiffEqCallbacks v4.11.0
[0b91fe84] DisplayAs v0.1.6
[f6369f11] ForwardDiff v1.3.1
[682c06a0] JSON v1.3.0
[23fbe1c1] Latexify v0.16.10
[98b081ad] Literate v2.21.0
⌅ [961ee093] ModelingToolkit v10.31.2
[77ba4419] NaNMath v1.1.3
[8913a72c] NonlinearSolve v4.13.0
[1dea7af3] OrdinaryDiffEq v6.105.0
[91a5bcdd] Plots v1.41.4
[33c8b6b6] ProgressLogging v0.1.6
[9672c7b4] SteadyStateDiffEq v2.9.0
⌅ [0c5d862f] Symbolics v6.58.0
[37e2e46d] LinearAlgebra v1.12.0
Info Packages marked with ⌅ have new versions available but compatibility constraints restrict them from upgrading. To see why use `status --outdated`This notebook was generated using Literate.jl.