using ProgressLogging
using OrdinaryDiffEq
using ModelingToolkit
using DiffEqCallbacks
using Plots
using ECMEDox
using ECMEDox: second, Hz, μM, nM, mV
Plots.default(lw=1.5)Hypoxia reperfusion simulation
tend = 100.0second
bcl = 1.0second
@named sys = build_model()
u0 = build_u0(sys)
sts = unknowns(sys)
alg = KenCarp47()
@unpack iStim = sys
stim! = build_stim_callbacks(iStim, tend; period=bcl)
prob = ODEProblem(sys, [u0; sys.O2_o => 6nM], tend)ODEProblem with uType Vector{Float64} and tType Float64. In-place: true Initialization status: FULLY_DETERMINED Non-trivial mass matrix: false timespan: (0.0, 100000.0) u0: 64-element Vector{Float64}: 2.196435053752864 0.0007273589705197244 0.000981691808598968 245.22202099807583 281.0719264404058 197.06621753790645 34.41477140951692 60.37913837798986 229.2919970960533 22.321405235243013 ⋮ 23.148552252520883 0.6928662120941113 0.20648605639609985 1295.5364065086924 1299.7940884726063 0.20381438659933854 145551.11317854663 10276.480036234318 -85.29107641956527
reoxygen! = (integrator) -> begin
integrator.ps[sys.O2_o] = 6μM
set_proposed_dt!(integrator, 1e-6)
end
cbs = CallbackSet(stim!, PresetTimeCallback(50.0second, reoxygen!))SciMLBase.CallbackSet{Tuple{}, Tuple{SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}}, ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}, DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}}, ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}, DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), Main.var"##277".var"#2#3"}, Main.var"##277".var"#2#3", DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), Main.var"##277".var"#2#3"}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}}}((), (SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}}, ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}, DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}}(0.0:1000.0:100000.0, true, SciMLBase.INITIALIZE_DEFAULT, ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}(-80.0, 0.5, iStim(t))), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}(-80.0, 0.5, iStim(t)), DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}}(0.0:1000.0:100000.0, true, SciMLBase.INITIALIZE_DEFAULT, ECMEDox.var"#4#5"{Float64, Float64, Symbolics.Num}(-80.0, 0.5, iStim(t))), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}}, ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}, DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}}(0.5:1000.0:100000.5, true, SciMLBase.INITIALIZE_DEFAULT, ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}(0.0, 0.5, iStim(t))), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}(0.0, 0.5, iStim(t)), DiffEqCallbacks.PresetTimeFunction{StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}, typeof(SciMLBase.INITIALIZE_DEFAULT), ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}}(0.5:1000.0:100000.5, true, SciMLBase.INITIALIZE_DEFAULT, ECMEDox.var"#6#7"{Float64, Float64, Symbolics.Num}(0.0, 0.5, iStim(t))), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), Main.var"##277".var"#2#3"}, Main.var"##277".var"#2#3", DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), Main.var"##277".var"#2#3"}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), Main.var"##277".var"#2#3"}([50000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##277".var"#2#3"()), Main.var"##277".var"#2#3"(), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), Main.var"##277".var"#2#3"}([50000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##277".var"#2#3"()), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ())))@time sol = solve(prob, alg; progress=true, callback=cbs, saveat=0.1second); 9.769951 seconds (21.75 M allocations: 1.277 GiB, 4.22% gc time, 82.22% compilation time)@unpack vm, dpsi, atp_i, adp_i = sys
pl_mmp = plot(sol, idxs=dpsi, lab=false, title="(A) Mito. memb. potential", xlabel="", ylabel="Voltage (mV)")
pl_mmp = vline!(pl_mmp, [50.0second], lines=(:dash, :black), lab=false)
pl_vm = plot(sol, idxs=vm, lab=false, title="(B) Action potential", xlabel="", ylabel="Voltage (mV)")
pl_vm = vline!(pl_vm, [50.0second], lines=(:dash, :black), lab=false)
pl_atp = plot(sol, idxs=atp_i/1000, lab=false, title="(C) ATP", xlabel="", ylabel="Conc. (mM)")
pl_atp = vline!(pl_atp, [50.0second], lines=(:dash, :black), lab=false)
@unpack cit, isoc, oaa, akg, scoa, suc, fum, mal = sys
pl_cac = plot(sol, idxs=[cit, isoc, oaa, akg, scoa, suc, fum, mal], legend=:right, title="(D) CAC intermediates", xlabel="Time (ms)", ylabel="Conc. (μM)")
pl_cac = vline!(pl_cac, [50.0second], lines=(:dash, :black), lab=false)
@unpack Q_n, SQn, QH2_n, QH2_p, Q_p, fes_ox, fes_rd, cytc_ox, cytc_rd = sys
pl_q = plot(sol, idxs=[Q_n, Q_p, SQn, QH2_n, QH2_p], title="(E) Q cycle", legend=:left, xlabel="Time (ms)", ylabel="Conc. (μM)")
pl_q = vline!(pl_q, [50.0second], lines=(:dash, :black), lab=false)
pl_ros = plot(sol, idxs=100 * sys.vROS / (sys.vO2 + sys.vROS), title="(F) ROS generation", lab=false, xlabel="Time (ms)", ylabel="Fraction of O2 consumption (%)", ylims=(0, 100))
pl_ros = vline!(pl_ros, [50.0second], lines=(:dash, :black), lab=false)
plot(pl_mmp, pl_vm, pl_atp, pl_cac, pl_q, pl_ros, size=(1200, 800))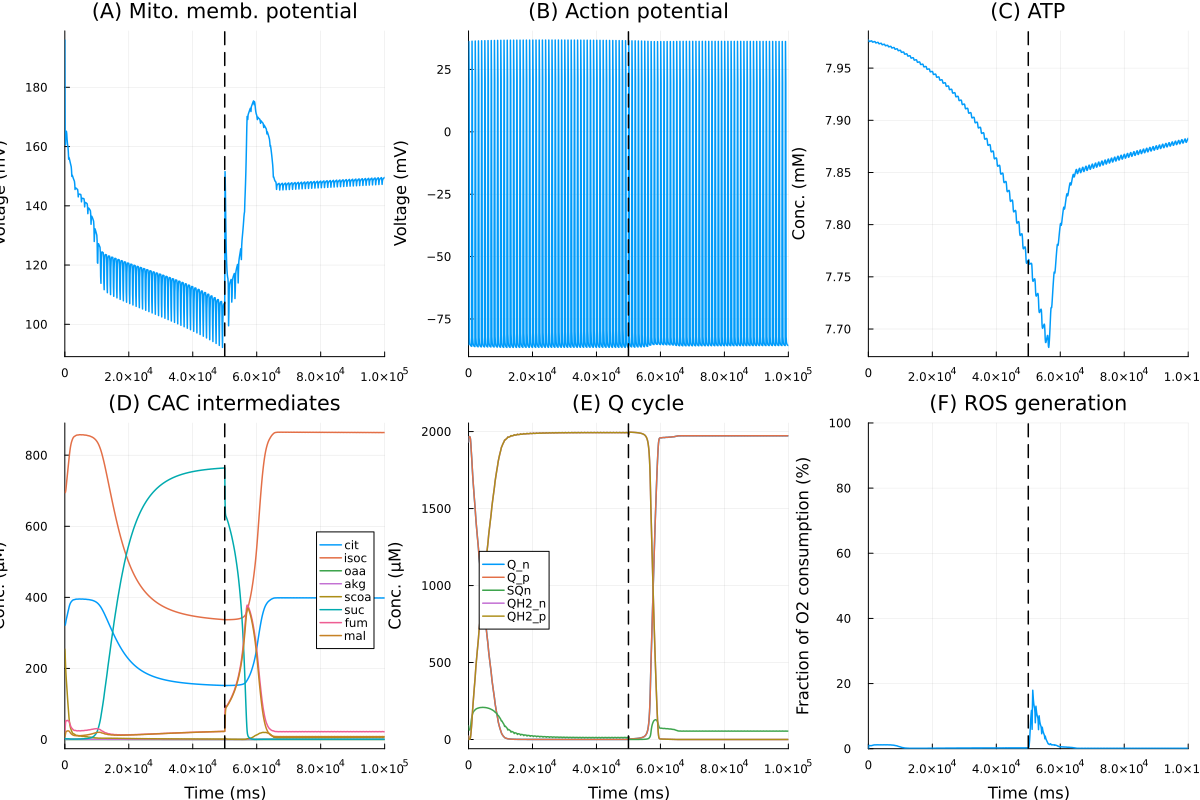
MMP
@unpack vm, dpsi, atp_i, adp_i = sys
pl_mmp = plot(sol, idxs=dpsi, lab=false, title="(A) Mito. memb. potential", xlabel="", ylabel="Voltage (mV)")
vline!(pl_mmp, [50.0second], lines=(:dash, :black), lab=false)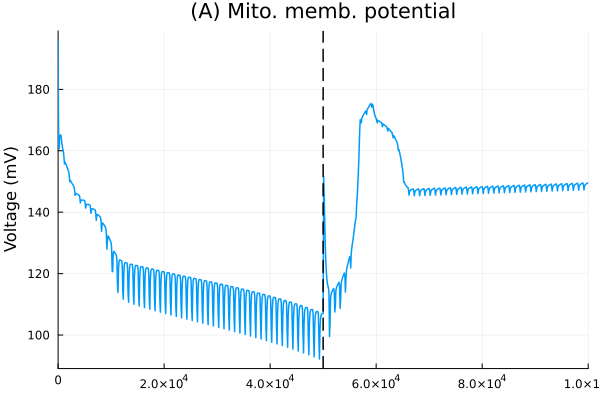
Action potential
pl_vm = plot(sol, idxs=vm, lab=false, title="(B) Action potential", xlabel="", ylabel="Voltage (mV)")
vline!(pl_vm, [50.0second], lines=(:dash, :black), lab=false)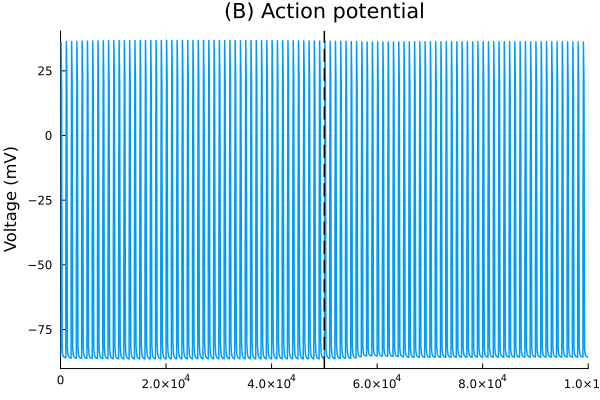
ATP
pl_atp = plot(sol, idxs=atp_i/1000, lab=false, title="(C) ATP", xlabel="", ylabel="Conc. (mM)")
vline!(pl_atp, [50.0second], lines=(:dash, :black), lab=false)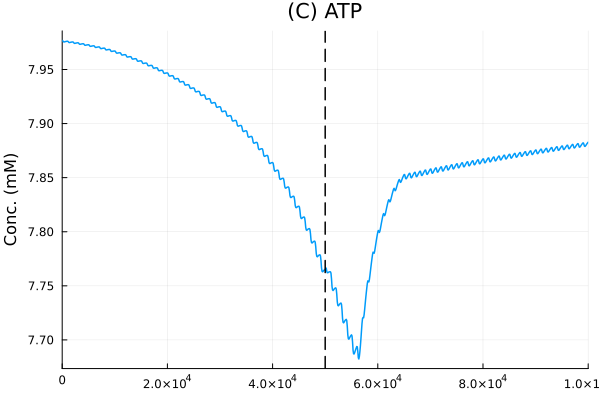
CAC
@unpack cit, isoc, oaa, akg, scoa, suc, fum, mal, nadh_m = sys
pl_cac = plot(sol, idxs=[cit, isoc, oaa, akg, scoa, suc, fum, mal, nadh_m], legend=:right, title="(D) CAC intermediates", xlabel="Time (ms)", ylabel="Conc. (μM)")
vline!(pl_cac, [50.0second], lines=(:dash, :black), lab=false)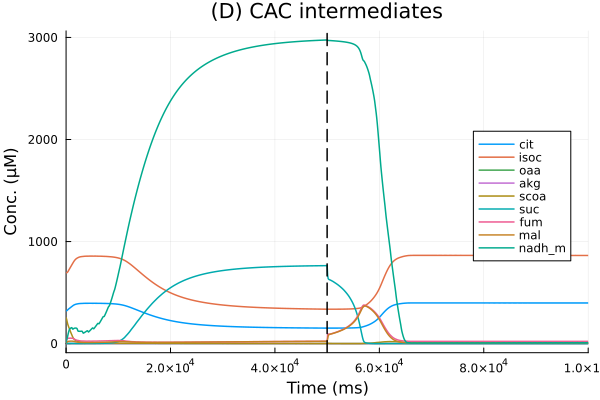
CAC flux
pl = plot(sol, idxs=[sys.vSDH, sys.vAAT, sys.vMDH, sys.vIDH])
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)
Q cycle
@unpack Q_n, SQn, QH2_n, QH2_p, Q_p, fes_ox, fes_rd, cytc_ox, cytc_rd = sys
pl_q = plot(sol, idxs=[Q_n, Q_p, SQn, QH2_n, QH2_p], title="(E) Q cycle", legend=:left, xlabel="Time (ms)", ylabel="Conc. (μM)")
vline!(pl_q, [50.0second], lines=(:dash, :black), lab=false)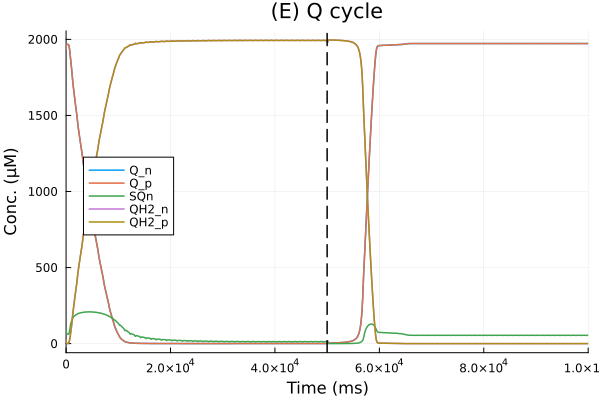
pl = plot(sol, idxs=[fes_ox, fes_rd, cytc_ox, cytc_rd], title="Q cycle downstream", legend=:left, xlabel="Time (ms)", ylabel="Conc. (μM)")
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)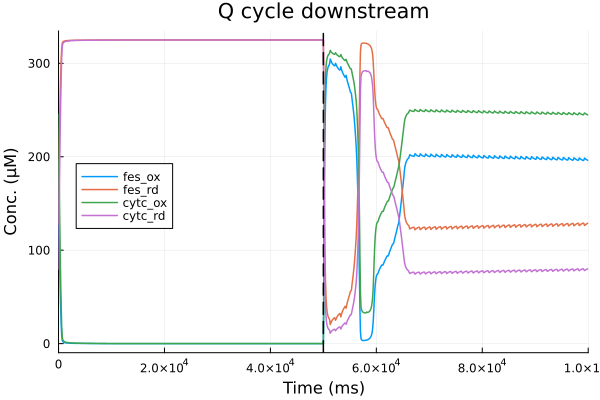
Proton pumping
pl = plot(sol, idxs=[sys.vHresC1, sys.vHresC3, sys.vHresC4], title="Proton pumping", legend=:left, xlabel="Time (ms)", ylabel="Rate (μM/ms)")
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)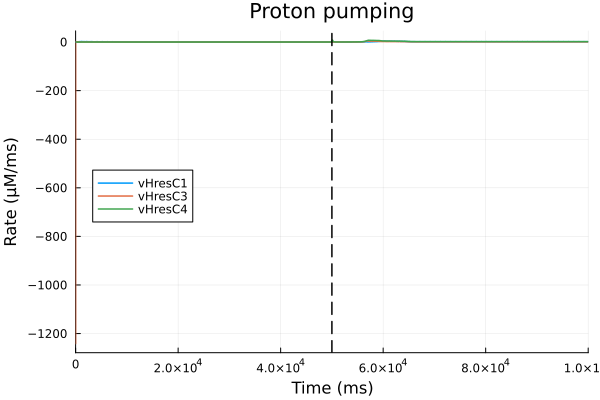
Mito oxygen concentration
pl = plot(sol, idxs=sys.O2)
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)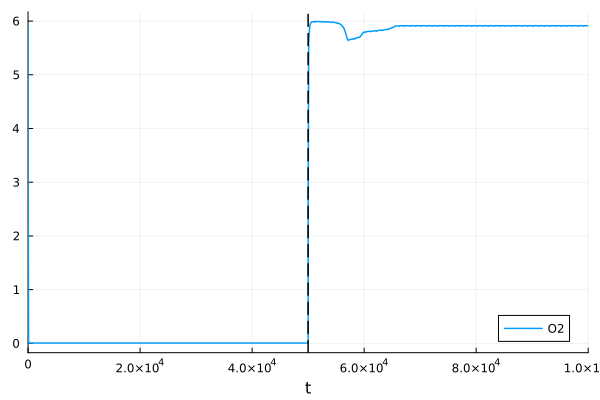
O2 shunt
pl_ros = plot(sol, idxs=100 * sys.vROS / (sys.vO2 + sys.vROS), title="(F) ROS generation", lab=false, xlabel="Time (ms)", ylabel="Fraction of O2 consumption (%)", ylims=(0, 100))
vline!(pl_ros, [50.0second], lines=(:dash, :black), lab=false)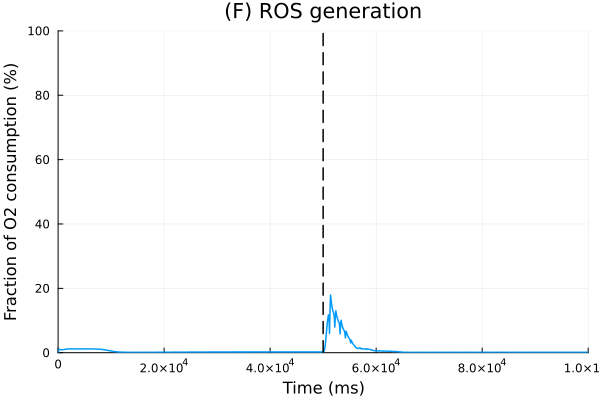
Superoxide production
pl = plot(sol, idxs=[sys.vROSC1, sys.vROSIf, sys.vROSIq, sys.vROSC3], ylims=(0.0, 0.05))
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)
Superoxide concentrations
pl = plot(sol, idxs=[sys.sox_m, sys.sox_i])
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)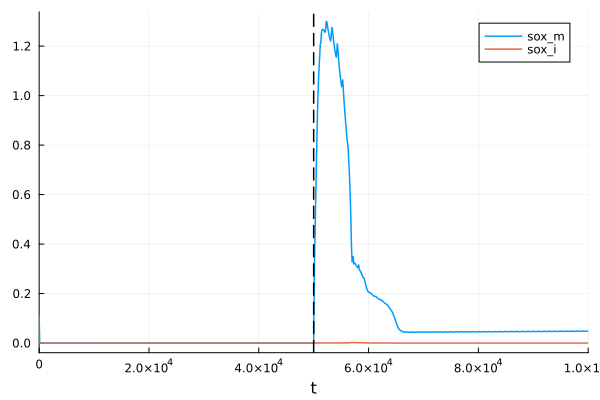
Semiquinone from Complex III Qo
pl = plot(sol, idxs=[sys.SQp])
vline!(pl, [50.0second], lines=(:dash, :black), lab=false)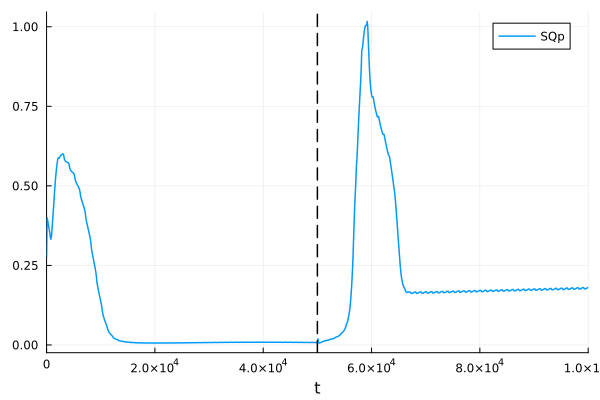
This notebook was generated using Literate.jl.