Solving Ordinary Differential Equations (ODEs) in Python

Source: Scipy’s documentation.

odeint(model,y0,t,args=(...))

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
%matplotlib inline

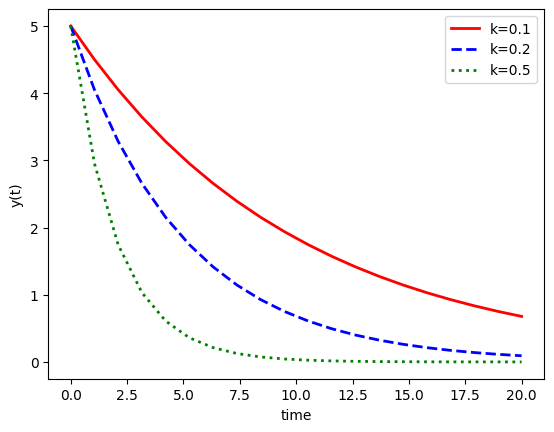
Exponential decays

# function that returns dy/dt
def model(t, y, k):
    dydt = -k * y[0]
    return [dydt]

# initial condition
y0 = [5]
tspan = (0., 20.)

# solve ODEs
y1 = solve_ivp(model, tspan, y0, args=(0.1,), dense_output=True)
y2 = solve_ivp(model, tspan, y0, args=(0.2,), dense_output=True)
y3 = solve_ivp(model, tspan, y0, args=(0.5,), dense_output=True)

ts = np.linspace(tspan[0], tspan[1], 20)
# plot results
plt.figure()
plt.plot(ts, y1.sol(ts).T, 'r-',linewidth=2,label='k=0.1')
plt.plot(ts, y2.sol(ts).T, 'b--',linewidth=2,label='k=0.2')
plt.plot(ts, y3.sol(ts).T, 'g:',linewidth=2,label='k=0.5')
plt.xlabel('time')
plt.ylabel('y(t)')
plt.legend()

<matplotlib.legend.Legend at 0x7f5aac1305d0>

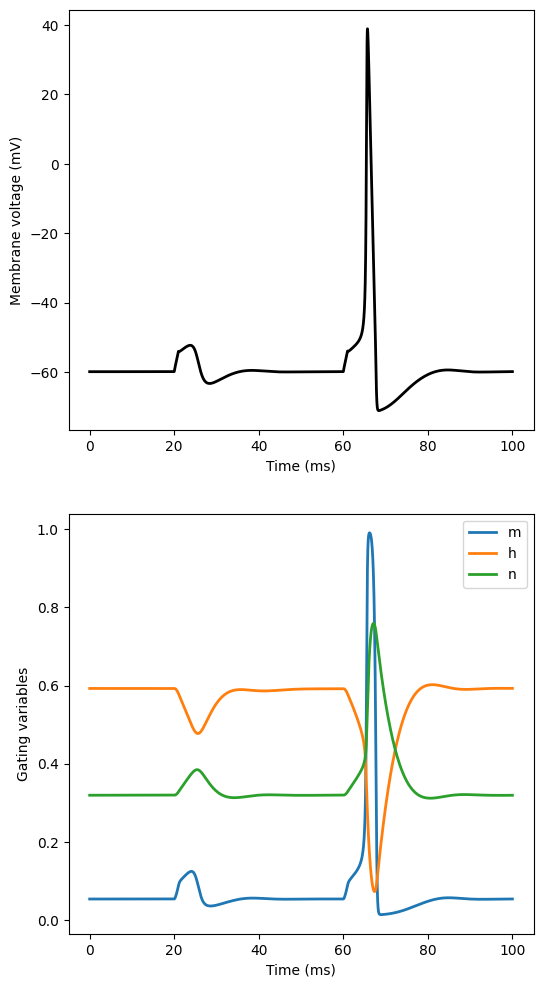
Hodgkin-Huxley electrophysiology model

"""
Hodgkin-Huxley model of excitable barnacle muscle fiber
reviewed in Rinzel (1990) Bulletin of Mathematical Biology 52 pp. 5-23.
"""
from math import exp, expm1

def get_iStim(t):
    return (20 < t <= 21) * -6.8 + (60 < t <= 61) * -6.9

# Model
def hh_rhs(t, y, p):
    # Constants
    E_N = p['E_N']  # Reversal potential of Na
    E_K = p['E_K']  # Reversal potential of K
    E_LEAK = p['E_LEAK']  # Reversal potential of leaky channels
    G_N_BAR = p['G_N_BAR']  # Max. Na channel conductance
    G_K_BAR = p['G_K_BAR'] # Max. K channel conductance
    G_LEAK = p['G_LEAK']  # Max. leak channel conductance
    C_M = p['C_M']  # membrane capacitance

    # Equations
    v, m, h, n = y

    mAlfaV = -0.10 * (v + 35)
    mAlfa = mAlfaV / expm1(mAlfaV)
    mBeta = 4.0 * exp(-(v + 60) / 18.0)
    dm = -(mAlfa + mBeta) * m + mAlfa
    
    hAlfa = 0.07 * exp(-(v+60)/20)
    hBeta = 1 / (exp(-(v+30)/10) + 1)
    dh  = -(hAlfa + hBeta) * h + hAlfa
    
    iNa = G_N_BAR * (v - E_N) * (m**3) * h

    nAlfaV = -0.1 * (v+50)
    nAlfa = 0.1 * nAlfaV / expm1(nAlfaV)
    nBeta = 0.125 * exp( -(v+60) / 80)
    dn  = -(nAlfa + nBeta) * n + nAlfa
    
    iK = G_K_BAR * (v - E_K) * (n**4)
    iLeak = G_LEAK * (v - E_LEAK)
    iSt = get_iStim(t)
    dv = -(iNa + iK + iLeak + iSt) / C_M

    return [dv, dm, dh, dn]

# Initial conditions
y0 = v, m, h, n = -59.8977, 0.0536, 0.5925, 0.3192

# Parameters
p = {'E_N': 55,     # Reversal potential of Na
     'E_K': -72,    # Reversal potential of K
     'E_LEAK': -49, # Reversal potential of leaky channels
     'G_N_BAR': 120,# Max. Na channel conductance
     'G_K_BAR': 36, # Max. K channel conductance
     'G_LEAK': 0.3, # Max. leak channel conductance
     'C_M': 1.0}    # membrane capacitance

# time span
tStart, tEnd = 0, 100

%%time
sol2 = solve_ivp(hh_rhs, (tStart, tEnd), y0, args=(p, ), method='LSODA', rtol=1e-7, atol=1e-7)

CPU times: user 31 ms, sys: 3.78 ms, total: 34.8 ms
Wall time: 30.3 ms

# Plotting
fig, axs = plt.subplots(nrows=2, figsize=(6, 12))
axs[0].plot(sol2.t, sol2.y[0, :].T, 'k-', linewidth=2)
axs[0].set_xlabel("Time (ms)")
axs[0].set_ylabel("Membrane voltage (mV)")
axs[1].plot(sol2.t, sol2.y[1:4, :].T, linewidth=2, label=["m", "h", "n"])
axs[1].set_xlabel("Time (ms)")
axs[1].set_ylabel("Gating variables")
axs[1].legend()

<matplotlib.legend.Legend at 0x7f5aac181990>