Schelling’s segregation model

Source: Agents.jl tutorial. Wikipedia

Agents : They belong to one of two groups (0 or 1).
Model : Each position of the grid can be occupied by at most one agent.
For each step
- If an agent has at least 3 neighbors belonging to the same group, then it is happy.
- If an agent is unhappy, it keeps moving to new locations until it is happy.

To define an agent type, we should make a mutable struct derived from AbstractAgent with 2 mandatory fields: - id::Int . The identifier number of the agent. - pos . For agents on a 2D grid, the position field should be a tuple of 2 integers.

On top of that, we could define other properties for the agents.

Setup

First, we create a 2D space with a Chebyshev metric. This leads to 8 neighboring positions per position (except at the edges of the grid).

using Agents
using Random
using CairoMakie
CairoMakie.activate!(px_per_unit = 1.0)


Update message: Agents v6

This is a new major version of Agents.jl with lots of cool stuff!
However, from this version onwards, we will stop posting update messages
to the REPL console!

If you want to be updated, follow this discourse post:

https://discourse.julialang.org/t/agents-jl-v6-releases-announcement-post/111678

(and see the CHANGELOG.md file online for a list of changes!)

The helper function below is adapted from Agents.abmvideo and correctly displays animations in Jupyter notebooks

function abmvio(model;
    dt = 1, framerate = 30, frames = 300, title = "", showstep = true,
    figure = (size = (600, 600),), axis = NamedTuple(),
    recordkwargs = (compression = 23, format ="mp4"), kwargs...
)
    # title and steps
    abmtime_obs = Observable(abmtime(model))
    if title ≠ "" && showstep
        t = lift(x -> title*", time = "*string(x), abmtime_obs)
    elseif showstep
        t = lift(x -> "time = "*string(x), abmtime_obs)
    else
        t = title
    end

    axis = (title = t, titlealign = :left, axis...)
    # First frame
    fig, ax, abmobs = abmplot(model; add_controls = false, warn_deprecation = false, figure, axis, kwargs...)
    resize_to_layout!(fig)
    # Animation
    Makie.Record(fig; framerate, recordkwargs...) do io
        for j in 1:frames-1
            recordframe!(io)
            Agents.step!(abmobs, dt)
            abmtime_obs[] = abmtime(model)
        end
        recordframe!(io)
    end
end

abmvio (generic function with 1 method)

Define the Agent type using the @agent macro. The agents inherit all properties of GridAgent{2} sicne they live on a 2D grid. They also have two properties: mood (happy or not) and group.

@agent struct SchellingAgent(GridAgent{2})
    mood::Bool = false ## true = happy
    group::Int ## the group does not have a default value!
end

Define the stepping function for the agent nearby_agents(agent, model) lists neighbors. If there are over 2 neighbors of the same group, make the agent happy. Else, the agent will move to a random empty position

function schelling_step!(agent::SchellingAgent, model)
    minhappy = model.min_to_be_happy
    count_neighbors_same_group = 0
    for neighbor in nearby_agents(agent, model)
        if agent.group == neighbor.group
            count_neighbors_same_group += 1
        end
    end
    if count_neighbors_same_group ≥ minhappy
        agent.mood = true ## The agent is happy
    else
        agent.mood = false
        move_agent_single!(agent, model) ## Move the agent to a random position
    end
    return nothing
end

schelling_step! (generic function with 1 method)

It is recommended to use a function to create the ABM for easily alter its parameters.

function init_schelling(; numagents = 300, griddims = (20, 20), min_to_be_happy = 3, seed = 2024)
    # Create a space for the agents to reside
    space = GridSpace(griddims)
    # Define parameters of the ABM
    properties = Dict(:min_to_be_happy => min_to_be_happy)
    rng = Random.Xoshiro(seed)
    # Create the model
    model = StandardABM(
        SchellingAgent, space;
        properties, rng,
        agent_step! = schelling_step!,
        container = Vector, ## agents are not removed, this is faster
        scheduler = Schedulers.Randomly()
    )

    # Populate the model with agents, adding equal amount of the two types of agents at random positions in the model.
    # We don't have to set the starting position. Agents.jl will choose a random position.
    for n in 1:numagents
        add_agent_single!(model; group = n < 300 / 2 ? 1 : 2)
    end
    return model
end

init_schelling (generic function with 1 method)

Running the model

model = init_schelling()

StandardABM with 300 agents of type SchellingAgent
 agents container: Vector
 space: GridSpace with size (20, 20), metric=chebyshev, periodic=true
 scheduler: Agents.Schedulers.Randomly
 properties: min_to_be_happy

The step!() function evolves the model forward. The run!() function is similar to step!() but also collects data along the simulation. Progress the model by one step.

step!(model)

StandardABM with 300 agents of type SchellingAgent
 agents container: Vector
 space: GridSpace with size (20, 20), metric=chebyshev, periodic=true
 scheduler: Agents.Schedulers.Randomly
 properties: min_to_be_happy

Progress the model by 3 steps

step!(model, 3)

StandardABM with 300 agents of type SchellingAgent
 agents container: Vector
 space: GridSpace with size (20, 20), metric=chebyshev, periodic=true
 scheduler: Agents.Schedulers.Randomly
 properties: min_to_be_happy

Progress the model until 90% of the agents are happy

happy90(model, time) = count(a -> a.mood == true, allagents(model))/nagents(model) ≥ 0.9
step!(model, happy90)

StandardABM with 300 agents of type SchellingAgent
 agents container: Vector
 space: GridSpace with size (20, 20), metric=chebyshev, periodic=true
 scheduler: Agents.Schedulers.Randomly
 properties: min_to_be_happy

How many steps are passed

abmtime(model)

Visualization

The abmplot() function visulizes the simulation result using Makie.jl. Some helper functions to identify agent groups.

groupcolor(a) = a.group == 1 ? :blue : :orange
groupmarker(a) = a.group == 1 ? :circle : :rect

groupmarker (generic function with 1 method)

Plot the initial conditions of the model

model = init_schelling()
figure, _ = abmplot(model; agent_color = groupcolor, agent_marker = groupmarker, agent_size = 15, axis=(;title = "Schelling's segregation model"))
figure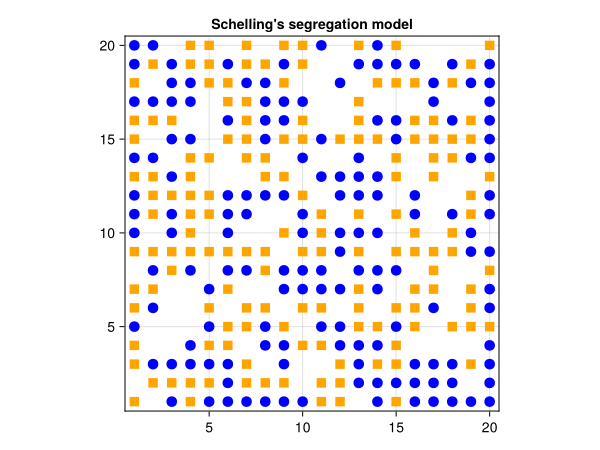

Let’s make an animation for the model evolution.

model = init_schelling()
vio = abmvio(model;
    agent_color = groupcolor,
    agent_marker = groupmarker,
    agent_size = 15,
    framerate = 4, frames = 20,
    title = "Schelling's segregation model"
)

vio |> display

Data analysis

The run!() function runs simulation and collects data in the DataFrame format. The adata (aggregated data) keyword selects fields we want to extract in the DataFrame.

x(agent) = agent.pos[1]
adata = [x, :mood, :group]
model = init_schelling()
adf, mdf = run!(model, 5; adata)
adf[end-10:end, :] ## display only the last few rows

11×5 DataFrame

Row	time	id	x	mood	group
	Int64	Int64	Int64	Bool	Int64
1	5	290	10	true	2
2	5	291	19	false	2
3	5	292	5	true	2
4	5	293	16	true	2
5	5	294	16	true	2
6	5	295	6	true	2
7	5	296	8	true	2
8	5	297	7	true	2
9	5	298	14	true	2
10	5	299	11	true	2
11	5	300	10	true	2

This notebook was generated using Literate.jl.