Fig 7.17 - MMSB

Goodwin oscillator model: Goodwin model (biology)

using ComponentArrays: ComponentArray
using SimpleUnPack
using OrdinaryDiffEq
using CairoMakie

function model717!(D, u, p, t)
    @unpack a, k, b, α, β, γ, δ, n = p
    @unpack X, Y, Z = u
    D.X = a / (k^n + Z^n) - b * X
    D.Y = α * X - β * Y
    D.Z = γ * Y - δ * Z
    nothing
end

model717! (generic function with 1 method)

ps717 = ComponentArray(
    a = 360.0,
    k = 1.368,
    b = 1.0,
    α = 1.0,
    β = 0.6,
    γ = 1.0,
    δ = 0.8,
    n = 12.0
)

u0 = ComponentArray(
    X = 0.0,
    Y = 0.0,
    Z = 0.0
)

tend = 35.0
prob717 = ODEProblem(model717!, u0, tend, ps717)
@time sol = solve(prob717, KenCarp47())

  2.379039 seconds (9.51 M allocations: 641.362 MiB, 6.60% gc time, 99.97% compilation time)

retcode: Success
Interpolation: 3rd order Hermite
t: 29-element Vector{Float64}:
  0.0
  9.999999999999999e-5
  0.0010999999999999998
  0.011099999999999997
  0.11109999999999996
  0.2607668329645834
  0.5215914083378239
  0.9265191831123549
  1.5792569045835068
  1.97361655727457
  ⋮
 20.67551016562918
 23.2308672254091
 25.024804375970536
 26.87259600744249
 28.834242807004994
 30.7958896065675
 33.098219255771276
 34.99807752330548
 35.0
u: 29-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(X = 1, Y = 2, Z = 3)}}}}:
 ComponentVector{Float64}(X = 0.0, Y = 0.0, Z = 0.0)
 ComponentVector{Float64}(X = 0.0008380069445124621, Y = 4.1900201048773956e-8, Z = 1.4477513491653054e-12)
 ComponentVector{Float64}(X = 0.00921346896413745, Y = 5.067222000164873e-6, Z = 1.8579076738792639e-9)
 ComponentVector{Float64}(X = 0.09250904681184341, Y = 0.0005132339782646043, Z = 1.8975588607166294e-6)
 ComponentVector{Float64}(X = 0.8812145539485637, Y = 0.04875819637395355, Z = 0.0017921487143668187)
 ComponentVector{Float64}(X = 1.923652662627426, Y = 0.24829621016031705, Z = 0.02119996856111633)
 ComponentVector{Float64}(X = 3.406037462238784, Y = 0.86815707181614, Z = 0.14550008091534836)
 ComponentVector{Float64}(X = 5.062348909590166, Y = 2.235103644299885, Z = 0.6450535786109586)
 ComponentVector{Float64}(X = 3.9398223047322123, Y = 4.3511465067681625, Z = 2.183260408411733)
 ComponentVector{Float64}(X = 2.6574445249438017, Y = 4.5693668388538695, Z = 3.118562939301336)
 ⋮
 ComponentVector{Float64}(X = 0.31807575198970656, Y = 1.4977167903212667, Z = 2.2136333878120027)
 ComponentVector{Float64}(X = 1.897880865830155, Y = 1.3412794438540068, Z = 1.4160479557500862)
 ComponentVector{Float64}(X = 0.64649416868638, Y = 1.836741425955782, Z = 2.16517331024345)
 ComponentVector{Float64}(X = 0.26552555648336185, Y = 0.9448691314463054, Z = 1.7062876427146694)
 ComponentVector{Float64}(X = 1.7827234915787002, Y = 1.968338699345517, Z = 1.732068347598522)
 ComponentVector{Float64}(X = 0.30915449418821705, Y = 1.4149798434917908, Z = 2.118883856386263)
 ComponentVector{Float64}(X = 1.769378286609491, Y = 1.2715573210786857, Z = 1.4152124834308464)
 ComponentVector{Float64}(X = 0.6021374857457749, Y = 1.772263796024488, Z = 2.1336449450999617)
 ComponentVector{Float64}(X = 0.6010582772331257, Y = 1.7713765836927573, Z = 2.1337696260238577)

fig = Figure()
ax = Axis(fig[1, 1],
    xlabel = "Time",
    ylabel = "Concentration",
    title = "Fig 7.17 (A)"
)

lines!(ax, 0..tend, t-> sol(t).X, label = "X")
lines!(ax, 0..tend, t-> sol(t).Y, label = "Y")
lines!(ax, 0..tend, t-> sol(t).Z, label = "Z")
axislegend(ax, position = :rt)
fig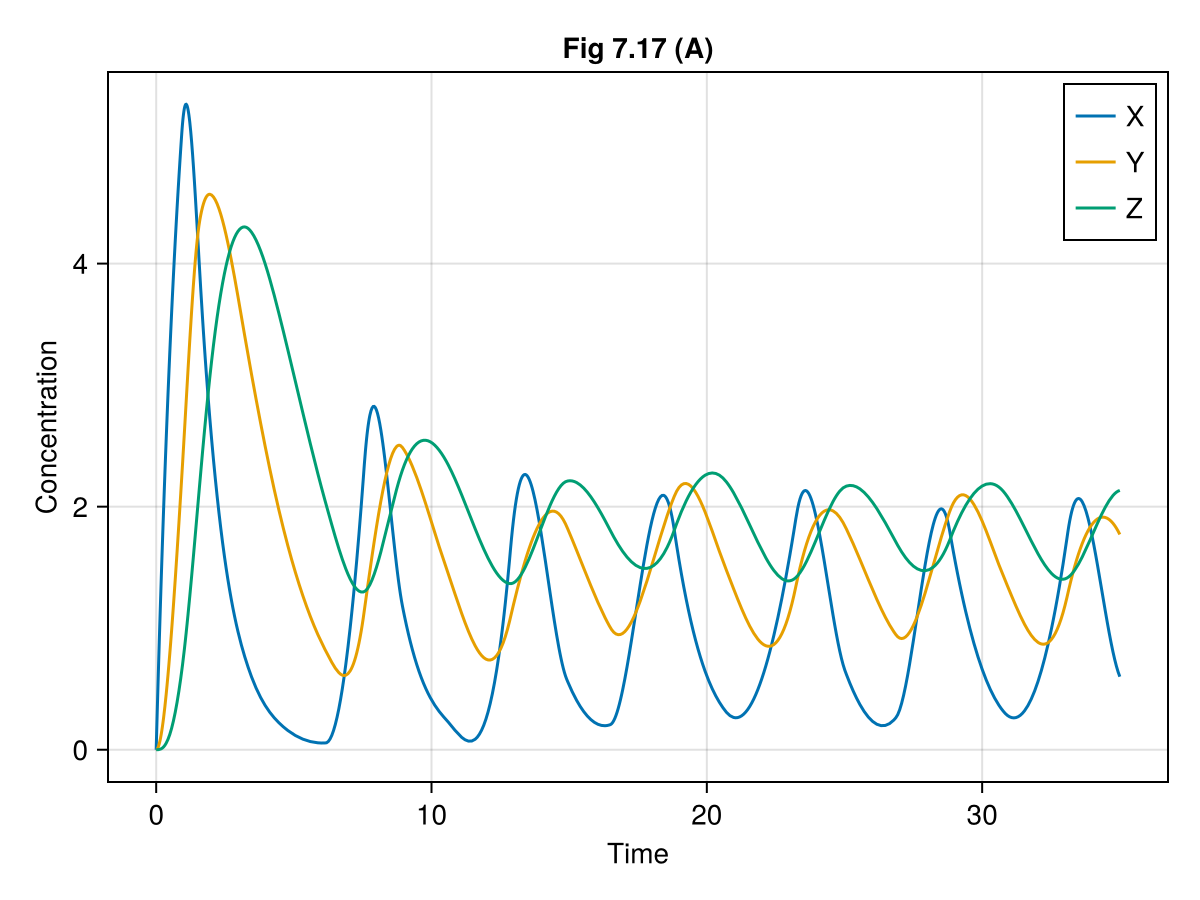

fig = Figure(size=(600, 600))
ax = Axis3(fig[1, 1],
    xlabel = "X",
    ylabel = "Y",
    zlabel = "Z",
    title = "Fig 7.17 (B)",
)
lines!(ax, sol, idxs=(1, 2, 3), color=:tomato)
fig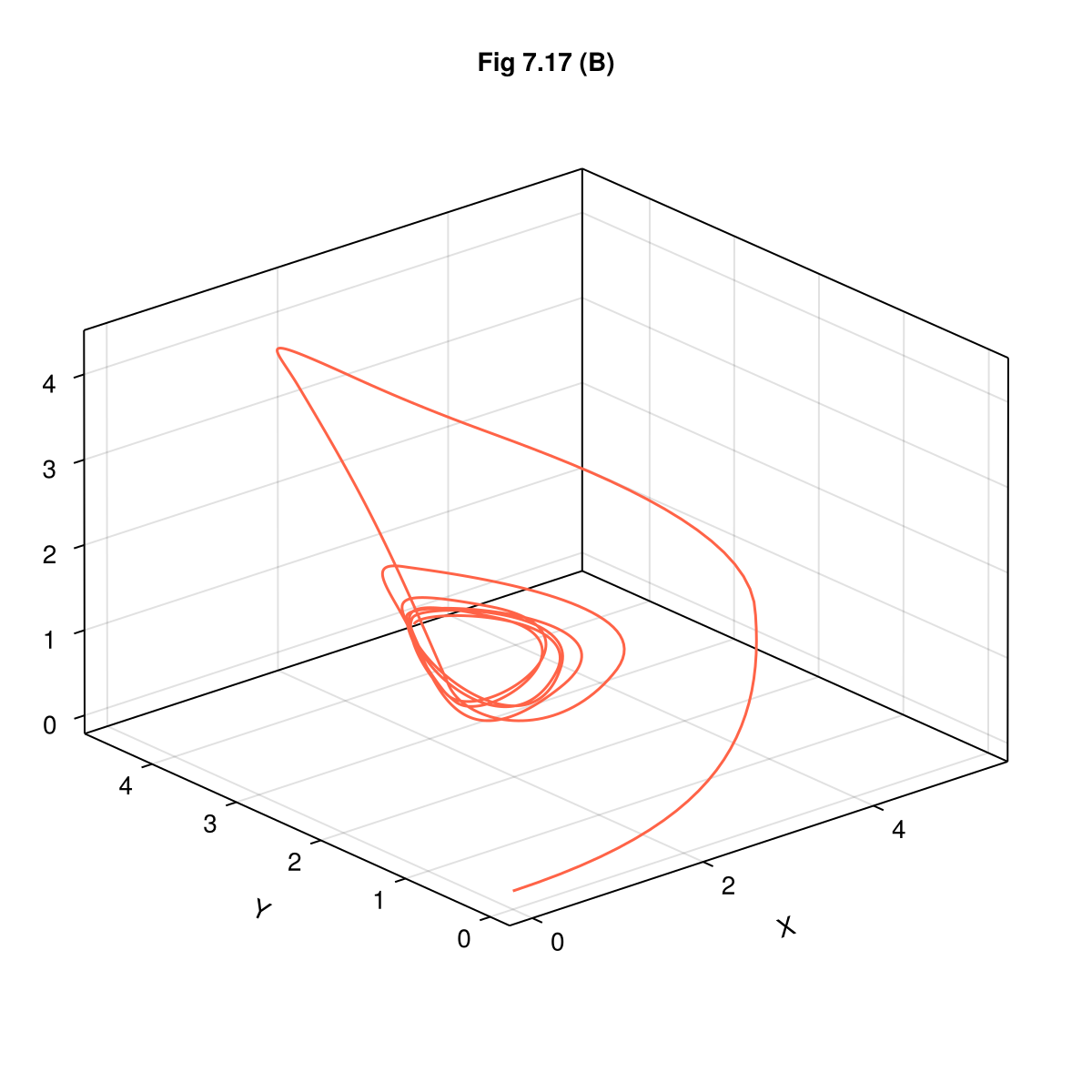

This notebook was generated using Literate.jl.