Fig 7.19 - MMSB

Circadian rhythm model

using OrdinaryDiffEq
using ComponentArrays: ComponentArray
using SimpleUnPack
using CairoMakie
using Peaks

function model719!(D, u, p, t)
    hil(x, k=one(x)) = x / (x + k)
    hil(x, k, n) = hil(x^n, k^n)
    @unpack vs, vm, vd, ks, kt1, kt2, v1, v2, v3, v4, k1, k2, k3, k4, ki, km1, kd, n = p
    @unpack M, P0, P1, P2, PN = u
    rM = vs * hil(ki, PN, n) - vm * hil(M, km1)
    rP01 = v1 * hil(P0, k1) - v2 * hil(P1, k2)
    rP12 = v3 * hil(P1, k3) - v4 * hil(P2, k4)
    rP2N = k1 * P2 - k2 * PN
    rP2 = vd * hil(P2, kd)
    D.M = rM
    D.P0 = ks * M - rP01
    D.P1 = rP01 - rP12
    D.P2 = rP12 - rP2N - rP2
    D.PN = rP2N
    nothing
end

model719! (generic function with 1 method)

ps719 = ComponentArray(
    vs = 0.76,
    vm = 0.65,
    vd = 0.95,
    ks = 0.38,
    kt1 = 1.9,
    kt2 = 1.3,
    v1 = 3.2,
    v2 = 1.58,
    v3 = 5.0,
    v4 = 2.5,
    k1 = 1.0,
    k2 = 1.0,
    k3 = 2.0,
    k4 = 2.0,
    ki = 1.0,
    km1 = 0.5,
    kd = 0.2,
    n = 4
)

ics719 = ComponentArray(
    M = 1.0,
    P0 = 1.0,
    P1 = 0.0,
    P2 = 0.0,
    PN = 0.0
)

tspan = (-50.0, 200.0)
prob719 = ODEProblem(model719!, ics719, tspan, ps719)

ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(M = 1, P0 = 2, P1 = 3, P2 = 4, PN = 5)}}} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (-50.0, 200.0)
u0: ComponentVector{Float64}(M = 1.0, P0 = 1.0, P1 = 0.0, P2 = 0.0, PN = 0.0)

@time sol719 = solve(prob719, KenCarp47())

  2.493530 seconds (9.84 M allocations: 657.300 MiB, 7.17% gc time, 99.87% compilation time)

retcode: Success
Interpolation: 3rd order Hermite
t: 64-element Vector{Float64}:
 -50.0
 -49.99911699979854
 -49.99028699778392
 -49.901986977637705
 -49.783244007548916
 -49.55889759975085
 -49.19009874666646
 -48.62549607810928
 -47.827649284265796
 -46.61550435301308
   ⋮
 170.21069615680824
 173.92652997282235
 176.8026888395213
 179.1722321513817
 182.3987254904936
 185.6252188296055
 189.40441066384113
 194.11914945761325
 200.0
u: 64-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(M = 1, P0 = 2, P1 = 3, P2 = 4, PN = 5)}}}}:
 ComponentVector{Float64}(M = 1.0, P0 = 1.0, P1 = 0.0, P2 = 0.0, PN = 0.0)
 ComponentVector{Float64}(M = 1.0002884283407238, P0 = 0.9989241516817039, P1 = 0.0014098808598433444, P2 = 1.5532943423400884e-6, PN = 4.575434694500928e-10)
 ComponentVector{Float64}(M = 1.0031706924451336, P0 = 0.9883180578456061, P1 = 0.015194548046177547, P2 = 0.00018078892912667567, PN = 5.901722146245127e-7)
 ComponentVector{Float64}(M = 1.0317951400715213, P0 = 0.8951637005366014, P1 = 0.12726661793736227, P2 = 0.012841007265373931, PN = 0.00045116871194621975)
 ComponentVector{Float64}(M = 1.0697426690179885, P0 = 0.7973604484844808, P1 = 0.22724681520993295, P2 = 0.04182817380039031, PN = 0.0034488973861230314)
 ComponentVector{Float64}(M = 1.1398573779321841, P0 = 0.6679159332171228, P1 = 0.32976147010852863, P2 = 0.09513345598615751, PN = 0.01690121607799914)
 ComponentVector{Float64}(M = 1.2511270712304134, P0 = 0.5487061844545659, P1 = 0.3869908363976394, P2 = 0.1541825576928421, PN = 0.0515875004080974)
 ComponentVector{Float64}(M = 1.4133839652504927, P0 = 0.4793930723137762, P1 = 0.3936092955845987, P2 = 0.19516082000863366, PN = 0.10695857635542344)
 ComponentVector{Float64}(M = 1.6292444812417795, P0 = 0.4765492842387035, P1 = 0.3926478123329067, P2 = 0.21817274958700394, PN = 0.16320318021476504)
 ComponentVector{Float64}(M = 1.9340660171123845, P0 = 0.5481512195277078, P1 = 0.4323973791328495, P2 = 0.25413847542814205, PN = 0.21596951787642718)
 ⋮
 ComponentVector{Float64}(M = 3.111403215563697, P0 = 1.6167556897272253, P1 = 1.206803065167913, P2 = 1.0360102048831914, PN = 0.9218105466379904)
 ComponentVector{Float64}(M = 2.1703556497513725, P0 = 1.4542363118742028, P1 = 1.370490264000554, P2 = 1.419540564368767, PN = 1.3287468804274165)
 ComponentVector{Float64}(M = 1.1707888582159087, P0 = 0.8817897439670889, P1 = 1.163393833799228, P2 = 1.4690984489755323, PN = 1.4731819697377455)
 ComponentVector{Float64}(M = 0.5732274596729989, P0 = 0.4834159505620909, P1 = 0.7998534409795105, P2 = 1.1843131836071763, PN = 1.315390471852149)
 ComponentVector{Float64}(M = 0.6778652370767524, P0 = 0.29081975679069366, P1 = 0.4114843959823488, P2 = 0.5308749359205049, PN = 0.7243430535680416)
 ComponentVector{Float64}(M = 1.5413095205083904, P0 = 0.41691737742621393, P1 = 0.3692228409677785, P2 = 0.26810115331338347, PN = 0.3177908049432321)
 ComponentVector{Float64}(M = 2.429972684058269, P0 = 0.770715566236851, P1 = 0.587455537598604, P2 = 0.38531423470161746, PN = 0.3399766703602397)
 ComponentVector{Float64}(M = 3.160917076269521, P0 = 1.396575364228953, P1 = 1.0152137606260336, P2 = 0.7971606171923917, PN = 0.6959703016019388)
 ComponentVector{Float64}(M = 2.1267961604567716, P0 = 1.4345697711884025, P1 = 1.3656848472883176, P2 = 1.4230393770351601, PN = 1.3349726774385093)

_total_P(sol) = sol.P0 .+ sol.P1 .+ sol.P2 .+ sol.PN
fig = Figure()
ax = Axis(fig[1, 1],
    xlabel = "Time",
    ylabel = "Concentration",
    title = "Fig 7.19 (A)"
)
lines!(ax, 0..tspan[2], t-> sol719(t).M, label = "M")
lines!(ax, 0..tspan[2], t-> sol719(t).PN, label = "Nuclear PER")
lines!(ax, 0..tspan[2], t->_total_P(sol719(t)), label = "Total PER")
axislegend(ax, position = :rt)
fig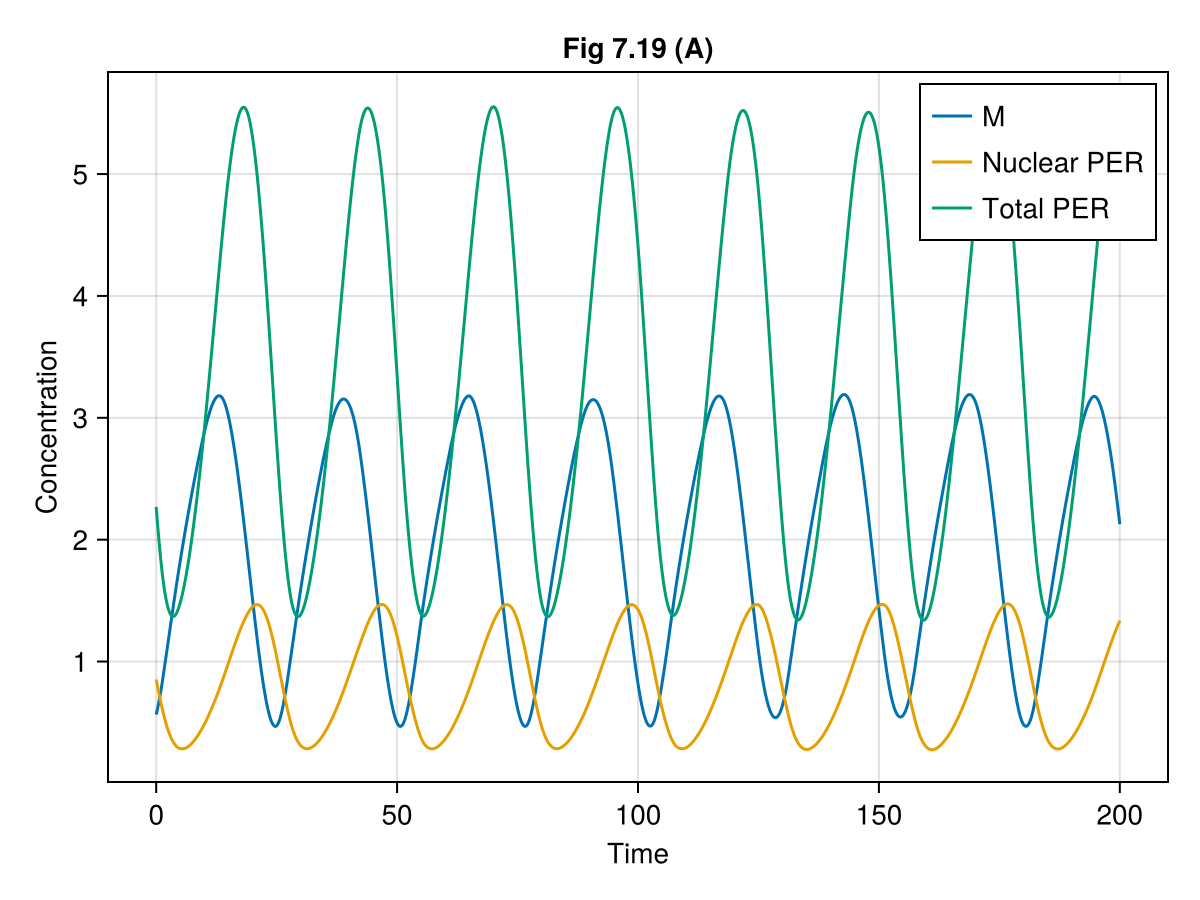

This notebook was generated using Literate.jl.