model of lac operon in E. coli
using ComponentArrays: ComponentArray
using SimpleUnPack
using DiffEqCallbacks
using OrdinaryDiffEq
using SteadyStateDiffEq
using CairoMakiefunction model707!(D, u, p, t)
hil(x, k) = x / (x + k)
hil(x, k, n) = hil(x^n, k^n)
@unpack Le, a1, RToverK1, K2, δM, δY, δL, c1, kL, KML, kg, KMg = p
@unpack M, Y, L = u
D.M = a1 / (1 + RToverK1 * (K2 / (K2 + L))^4) - δM * M
D.Y = c1 * M - δY * Y
D.L = kL * Y * hil(Le, KML) - 2kg * (Y/4) * hil(L, KMg) - δL * L
nothing
endmodel707! (generic function with 1 method)ps707 = ComponentArray(
δM = 0.48,
δY = 0.03,
δL = 0.02,
a1 = 0.29,
K2 = 2.92e6,
RToverK1 = 213.2,
c1 = 18.8,
kL = 6e4,
KML = 680.0,
kg = 3.6e3,
KMg = 7e5,
Le = 0.0,
)
ics707 = ComponentArray(
M = 0.01,
Y = 0.1,
L = 0.0,
)ComponentVector{Float64}(M = 0.01, Y = 0.1, L = 0.0)Events
affect_le1!(integrator) = integrator.p.Le = 50
affect_le2!(integrator) = integrator.p.Le = 100
affect_le3!(integrator) = integrator.p.Le = 150
affect_le4!(integrator) = integrator.p.Le = 0
event_le1 = PresetTimeCallback([500.0], affect_le1!)
event_le2 = PresetTimeCallback([1000.0], affect_le2!)
event_le3 = PresetTimeCallback([1500.0], affect_le3!)
event_le4 = PresetTimeCallback([2000.0], affect_le4!)
cbs = CallbackSet(event_le1, event_le2, event_le3, event_le4)SciMLBase.CallbackSet{Tuple{}, Tuple{SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le1!)}, typeof(Main.var"##249".affect_le1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le2!)}, typeof(Main.var"##249".affect_le2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le3!)}, typeof(Main.var"##249".affect_le3!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le3!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}, SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le4!)}, typeof(Main.var"##249".affect_le4!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le4!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}}}((), (SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le1!)}, typeof(Main.var"##249".affect_le1!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le1!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le1!)}([500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le1!), Main.var"##249".affect_le1!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le1!)}([500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le1!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le2!)}, typeof(Main.var"##249".affect_le2!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le2!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le2!)}([1000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le2!), Main.var"##249".affect_le2!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le2!)}([1000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le2!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le3!)}, typeof(Main.var"##249".affect_le3!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le3!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le3!)}([1500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le3!), Main.var"##249".affect_le3!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le3!)}([1500.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le3!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ()), SciMLBase.DiscreteCallback{DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le4!)}, typeof(Main.var"##249".affect_le4!), DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le4!)}, typeof(SciMLBase.FINALIZE_DEFAULT), Nothing, Tuple{}}(DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le4!)}([2000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le4!), Main.var"##249".affect_le4!, DiffEqCallbacks.PresetTimeFunction{Vector{Float64}, typeof(SciMLBase.INITIALIZE_DEFAULT), typeof(Main.var"##249".affect_le4!)}([2000.0], true, SciMLBase.INITIALIZE_DEFAULT, Main.var"##249".affect_le4!), SciMLBase.FINALIZE_DEFAULT, Bool[1, 1], nothing, ())))Fig 7.07 (A)¶
tend = 2500.0
prob707a = ODEProblem(model707!, ics707, tend, ps707)
@time sol = solve(prob707a, TRBDF2(), callback=cbs) 2.646401 seconds (9.90 M allocations: 665.815 MiB, 5.19% gc time, 99.94% compilation time)
retcode: Success
Interpolation: 3rd order Hermite
t: 240-element Vector{Float64}:
0.0
0.0030529842319340244
0.033582826551274265
0.33888124974467665
0.5477010840687467
1.232203566098551
1.5959869662444681
2.758101062245429
3.2693670361144287
4.798210419289836
⋮
2341.056374122994
2354.809120783752
2368.56186744451
2384.9266245640156
2402.6546813683526
2422.133329485706
2445.809794150764
2471.159897882199
2500.0
u: 240-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(M = 1, Y = 2, L = 3)}}}}:
ComponentVector{Float64}(M = 0.01, Y = 0.1, L = 0.0)
ComponentVector{Float64}(M = 0.009989486738585279, Y = 0.10056447448231473, L = 0.0)
ComponentVector{Float64}(M = 0.009885196281903036, Y = 0.10617340605644321, L = 0.0)
ComponentVector{Float64}(M = 0.008921417727493039, Y = 0.1588941805281965, L = 0.0)
ComponentVector{Float64}(M = 0.008339329567549437, Y = 0.19166694626706238, L = 0.0)
ComponentVector{Float64}(M = 0.006787931490691709, Y = 0.2838261093861022, L = 0.0)
ComponentVector{Float64}(M = 0.006151548282965767, Y = 0.324718480811908, L = 0.0)
ComponentVector{Float64}(M = 0.004713019403940765, Y = 0.42948674529969344, L = 0.0)
ComponentVector{Float64}(M = 0.004300286188421522, Y = 0.46589331472611184, L = 0.0)
ComponentVector{Float64}(M = 0.003518319014641902, Y = 0.554148300189143, L = 0.0)
⋮
ComponentVector{Float64}(M = 0.0028205726801400588, Y = 1.9241038351623863, L = 5.829399253601597e-7)
ComponentVector{Float64}(M = 0.0028205729625649244, Y = 1.8708769433755819, L = 4.1313191691717554e-7)
ComponentVector{Float64}(M = 0.002820572226050805, Y = 1.8357448193981682, L = 2.932525231469262e-7)
ComponentVector{Float64}(M = 0.002820575897916057, Y = 1.8090779353669042, L = 1.952287700754176e-7)
ComponentVector{Float64}(M = 0.002820567439376446, Y = 1.791797395692932, L = 1.2558790920225764e-7)
ComponentVector{Float64}(M = 0.0028205694744951578, Y = 1.7809525629578338, L = 7.742591125873105e-8)
ComponentVector{Float64}(M = 0.0028205729539459673, Y = 1.7740397872058438, L = 4.286151587842106e-8)
ComponentVector{Float64}(M = 0.002820572434854223, Y = 1.7705250237515948, L = 2.2738995730092172e-8)
ComponentVector{Float64}(M = 0.0028205716159487135, Y = 1.768770786799461, L = 1.1019125514760435e-8)fig = Figure()
ax = Axis(fig[1, 1], xlabel="Time (min)", ylabel="Concentration", title="Fig 7.7 (A)\nLac operon model in E. coli")
lines!(ax, 0..tend, t -> sol(t).Y, label="β-galactosidase monomer")
lines!(ax, 0..tend, t -> 50 * (500<=t<1000) + 100 * (1000<=t<1500) + 150 * (1500<=t<2000), label="External lactose")
axislegend(ax, position=:lt)
fig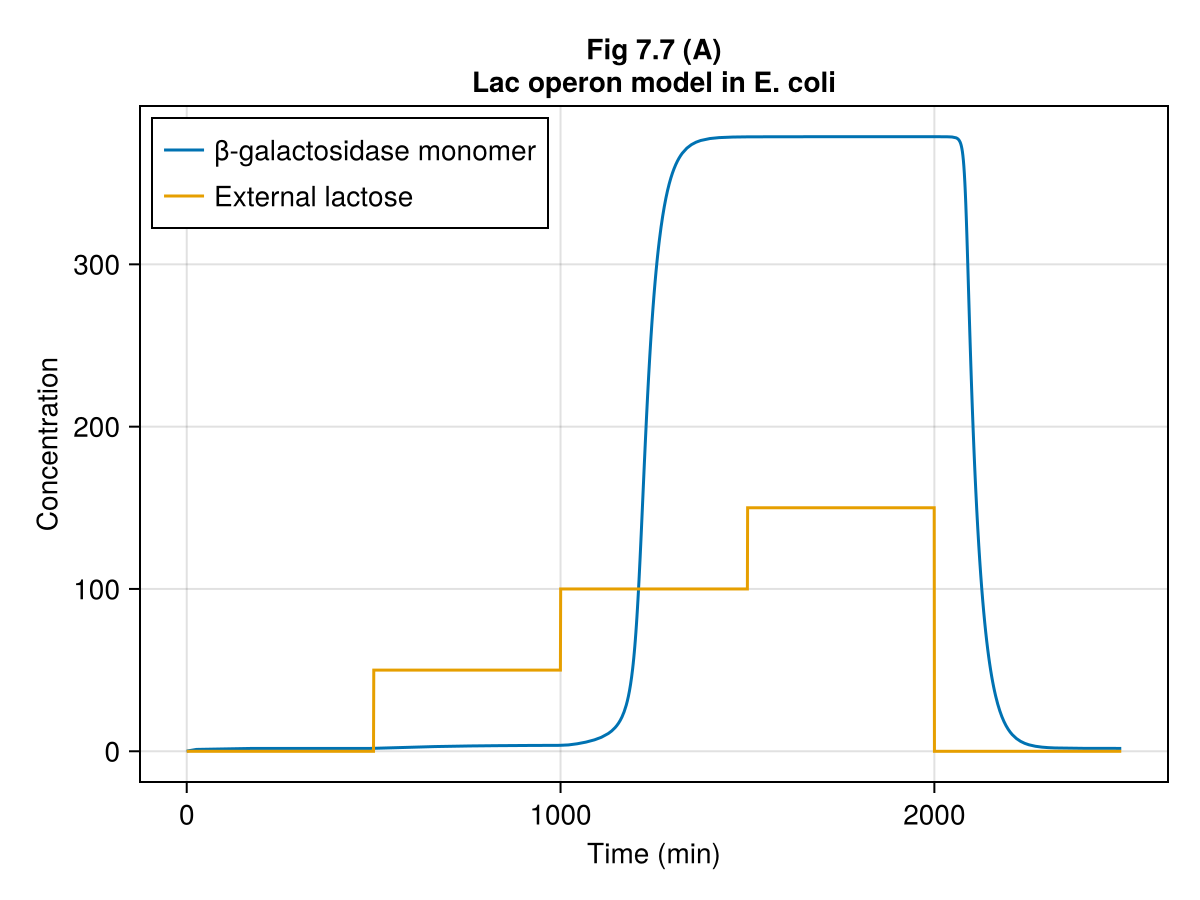
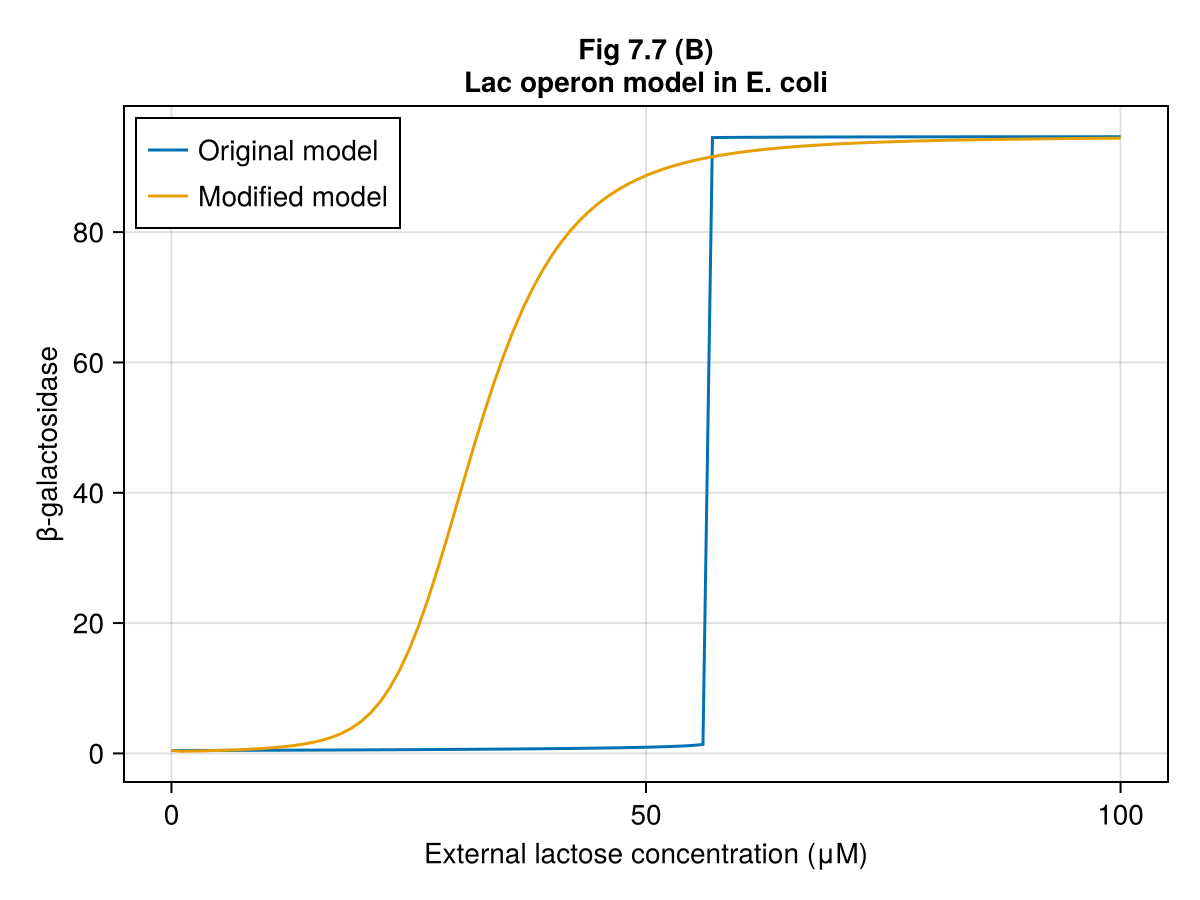
Fig 7.07 (B)¶
Compare the original model and the modified model
function model707b!(D, u, p, t)
hil(x, k) = x / (x + k)
hil(x, k, n) = hil(x^n, k^n)
@unpack Le, a1, RToverK1, K2, δM, δY, δL, c1, kL, KML, kg, KMg, Enz = p
@unpack M, Y, L = u
D.M = a1 / (1 + RToverK1 * (K2 / (K2 + L))^4) - δM * M
D.Y = c1 * M - δY * Y
D.L = 4kL * Enz * hil(Le, KML) - 2kg * Enz * hil(L, KMg) - δL * L
nothing
endmodel707b! (generic function with 1 method)ps707b = ComponentArray(ps707; Enz=40.0)
prob707a = SteadyStateProblem(model707!, ics707, ps707)
prob707b = SteadyStateProblem(model707b!, ics707, ps707b)
lerange = range(0, 100, 101)
eprob = EnsembleProblem(prob707a;
prob_func=(prob, i, repeat) -> remake(prob, p=ComponentArray(ps707; Le=lerange[i])),
output_func=(sol, i) -> (sol.u.Y / 4, false)
)
eprob_mod = EnsembleProblem(prob707b;
prob_func=(prob, i, repeat) -> remake(prob, p=ComponentArray(ps707b; Le=lerange[i])),
output_func=(sol, i) -> (sol.u.Y / 4, false)
)
alg = DynamicSS(TRBDF2())
@time sim = solve(eprob, alg; trajectories=length(lerange))
@time sim_mod = solve(eprob_mod, alg; trajectories=length(lerange))
fig = Figure()
ax = Axis(fig[1, 1], xlabel="External lactose concentration (μM)", ylabel="β-galactosidase", title="Fig 7.7 (B)\nLac operon model in E. coli")
lines!(ax, lerange, sim.u, label="Original model")
lines!(ax, lerange, sim_mod.u, label="Modified model")
axislegend(ax, position=:lt)
fig 1.664725 seconds (12.40 M allocations: 637.575 MiB, 4.40% gc time, 183.79% compilation time)
1.365428 seconds (8.91 M allocations: 457.654 MiB, 5.59% gc time, 182.44% compilation time)
This notebook was generated using Literate.jl.