Fig 6.19 - MMSB

Sine wave response of g-protein signalling pathway

using OrdinaryDiffEq
using ComponentArrays: ComponentArray
using SimpleUnPack
using CairoMakie

_l619(p, t) = p.lt + (p.lt / p.l_AMP) * cospi(2t / p.l_per)

function model619!(D, u, p, t)
    @unpack kRL, kRLm, kGa, kGd0, kG1, Rtotal, Gtotal, lt, l_per, l_AMP = p
    @unpack RL, Ga, Gd = u
    R = Rtotal - RL
    G = Gtotal - Ga - Gd
    Gbg = Ga + Gd
    L = _l619(p, t)
    v1 = kRL * R * L - kRLm * RL
    v2 = kGa * G * RL
    v3 = kGd0 * Ga
    v4 = kG1 * Gd * Gbg
    D.RL = v1
    D.Ga = v2 - v3
    D.Gd = v3 - v4
    nothing
end

model619! (generic function with 1 method)

ps619 = ComponentArray(
    kRL = 2e6,
    kRLm = 0.01,
    kGa = 1e-5,
    kGd0 = 0.11,
    kG1 = 1.0,
    Rtotal = 4e3,
    Gtotal = 1e4,
    lt = 1e-9,
    l_per = 200.0,
    l_AMP = 5.0
)

ics619 = ComponentArray(
    RL = 0.0,
    Ga = 0.0,
    Gd = 0.0,
)

tend = 1000.0
prob619 = ODEProblem(model619!, ics619, tend, ps619)

ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(RL = 1, Ga = 2, Gd = 3)}}} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 1000.0)
u0: ComponentVector{Float64}(RL = 0.0, Ga = 0.0, Gd = 0.0)

@time sol619 = solve(prob619, KenCarp47())

  3.311212 seconds (14.48 M allocations: 957.474 MiB, 6.32% gc time, 99.97% compilation time)

retcode: Success
Interpolation: 3rd order Hermite
t: 35-element Vector{Float64}:
    0.0
    9.999999999999999e-5
    0.0010999999999999998
    0.011099999999999997
    0.11109999999999996
    1.1110999999999995
    1.7783410641095294
    2.5496012241668646
    3.489348266210938
    5.018358008490838
    ⋮
  453.980831240806
  516.78217192869
  598.4144319044642
  651.8326828099439
  722.7302206874989
  817.9898513472049
  878.8660499153812
  952.959094919708
 1000.0
u: 35-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(RL = 1, Ga = 2, Gd = 3)}}}}:
 ComponentVector{Float64}(RL = 0.0, Ga = 0.0, Gd = 0.0)
 ComponentVector{Float64}(RL = 0.0009599994047994197, Ga = 4.799983909235566e-9, Gd = 2.1810340712763037e-14)
 ComponentVector{Float64}(RL = 0.01055992798077249, Ga = 5.807739068730109e-7, Gd = 2.4095579375448843e-11)
 ComponentVector{Float64}(RL = 0.1065526665173168, Ga = 5.911402427801946e-5, Gd = 2.4062810239941634e-8)
 ComponentVector{Float64}(RL = 1.0658253086705862, Ga = 0.005897964691156876, Gd = 2.4050861334995832e-5)
 ComponentVector{Float64}(RL = 10.593057250322973, Ga = 0.5665011661705285, Gd = 0.020909608509992024)
 ComponentVector{Float64}(RL = 16.88375124929373, Ga = 1.4129287994579152, Gd = 0.062130073340332874)
 ComponentVector{Float64}(RL = 24.089002626787657, Ga = 2.816733689653234, Gd = 0.09766273678837661)
 ComponentVector{Float64}(RL = 32.772495666323934, Ga = 5.084923744516445, Gd = 0.10718951694479543)
 ComponentVector{Float64}(RL = 46.67556913060146, Ga = 9.91462132039517, Gd = 0.1087463607373126)
 ⋮
 ComponentVector{Float64}(RL = 698.5369440370368, Ga = 598.7335110573752, Gd = 0.10997979827695435)
 ComponentVector{Float64}(RL = 634.0358322194525, Ga = 551.7985348571469, Gd = 0.1099780804814438)
 ComponentVector{Float64}(RL = 678.7343861992034, Ga = 572.4569388369919, Gd = 0.10997891099560256)
 ComponentVector{Float64}(RL = 702.4689890326028, Ga = 601.5971376236726, Gd = 0.10998029218611617)
 ComponentVector{Float64}(RL = 631.0933270943118, Ga = 548.5538910847856, Gd = 0.10997772800749415)
 ComponentVector{Float64}(RL = 699.3758765570768, Ga = 590.8151470650696, Gd = 0.10997956928277146)
 ComponentVector{Float64}(RL = 678.7037783856138, Ga = 588.2652748947846, Gd = 0.10997948983052451)
 ComponentVector{Float64}(RL = 630.7336022555951, Ga = 540.6637729620039, Gd = 0.1099776271853366)
 ComponentVector{Float64}(RL = 680.7104980533119, Ga = 574.4309789439747, Gd = 0.10997899651728757)

fig = Figure()
ax1 = Axis(fig[1, 1], xlabel="Time", ylabel="Concentration", title="Fig 6.19 A")
lines!(ax1, 0..tend, t -> sol619(t).Ga, label="Ga")
lines!(ax1, 0..tend, t -> _l619(ps619, t) * 1E12, label=L"L \cdot 10^{12}")
axislegend(ax1, position=:rb)
fig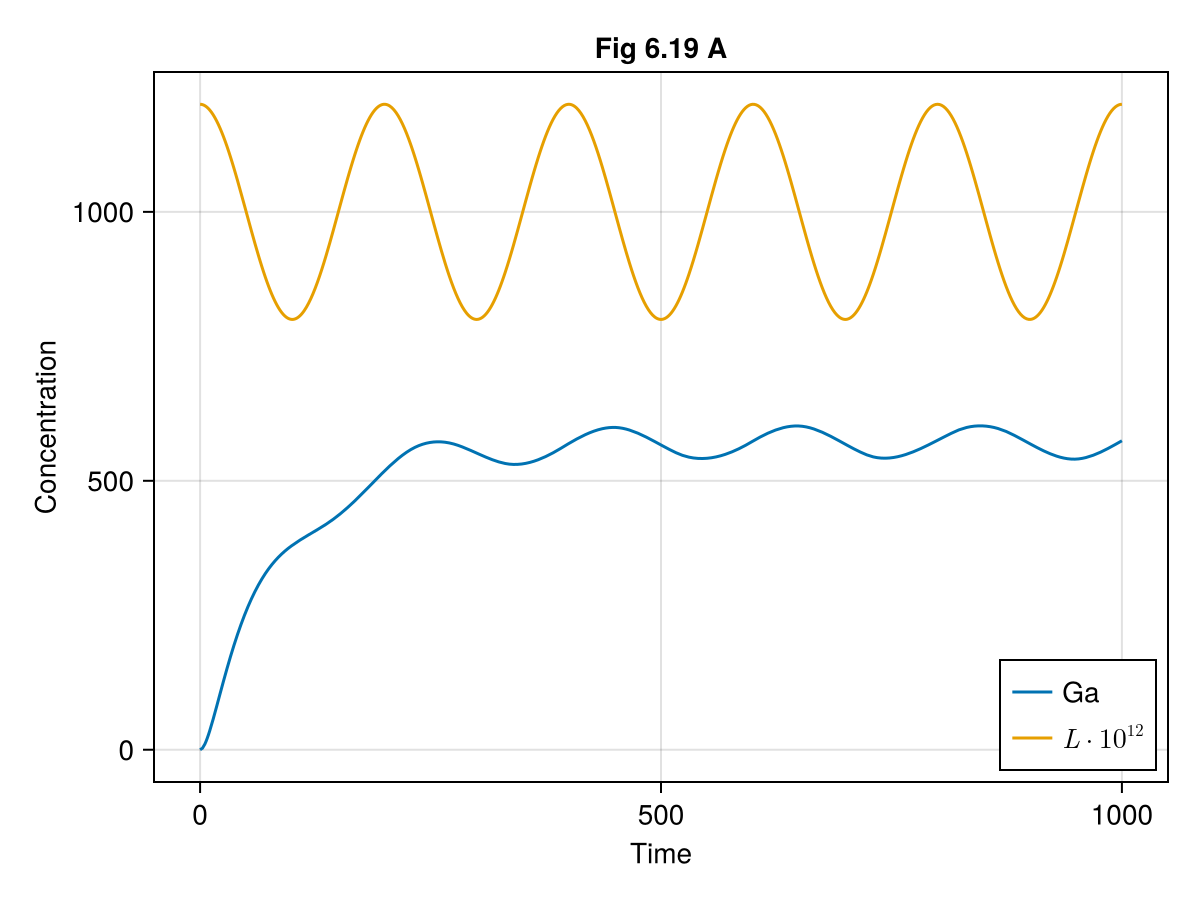

This notebook was generated using Literate.jl.