Stochastic simulations

Gillespie Algorithm¶

using CairoMakie
using DataInterpolations: LinearInterpolation
using StatsBase: Weights, sample
using Statistics: mean
using Random
Random.seed!(2024)

Random.TaskLocalRNG()

Do-it-yourself¶

Stochastic chemical reaction: Gillespie Algorithm (direct and first reaction method) Adapted from: Chemical and Biomedical Engineering Calculations Using Python Ch.4-3

function ssa_alg(model, u0::AbstractVector, tend, p, stoich; tstart=zero(tend), method=:direct)
    t = tstart   ## Current time
    ts = [t]     ## Time points
    u = copy(u0) ## Current state
    us = copy(u') ## States over time
    while t < tend
        a = model(u, p, t)               ## propensities
        if method == :direct
            dt = randexp() / sum(a)          ## Time step for the direct method
            du = sample(stoich, Weights(a))  ## Choose the stoichiometry for the next reaction
        elseif method == :first
            dts = randexp(length(a)) ./ a   ## time scales of all reactions
            i = argmin(dts)                 ## Choose the most recent reaction to occur
            dt = dts[i]
            du = stoich[i]
        else
            error("Method should be either :direct or :first")
        end
        u .+= du   ## Update time
        t += dt    ## Update time
        us = [us; u']  ## Append state
        push!(ts, t)   ## Append time point
    end
    return (t=ts, u=us)
end

ssa_alg (generic function with 1 method)

Propensity model for this example reaction. Reaction of A <-> B with rate constants k1 & k2

model(u, p, t) = [p.k1 * u[1], p.k2 * u[2]]

model (generic function with 1 method)

parameters = (k1=1.0, k2=0.5)

(k1 = 1.0, k2 = 0.5)

Stoichiometry for each reaction

stoich = [[-1, 1], [1, -1]]

2-element Vector{Vector{Int64}}:
 [-1, 1]
 [1, -1]

Initial conditions (Usually discrete values)

u0 = [200, 0]

2-element Vector{Int64}:
 200
   0

Simulation time

tend = 10.0

10.0

Solve the problem using both direct and first reaction method

@time soldirect = ssa_alg(model, u0, tend, parameters, stoich; method=:direct)
@time solfirst = ssa_alg(model, u0, tend, parameters, stoich; method=:first)

  0.186343 seconds (688.01 k allocations: 61.390 MiB, 7.54% gc time, 98.37% compilation time)
  0.012432 seconds (9.95 k allocations: 14.957 MiB, 88.65% gc time)

(t = [0.0, 0.006874672879606227, 0.0070050915014185, 0.01329115182676454, 0.015335530116774018, 0.01942319769041779, 0.021346508038833215, 0.02345030020299408, 0.025497753122539372, 0.02734483697039726  …  9.937773197389458, 9.938360255993572, 9.964450740930666, 9.96564917153764, 9.975440668199402, 9.978594329657025, 9.982318425245289, 9.987213207313044, 9.995833233887383, 10.024199143896238], u = [200 0; 199 1; … ; 75 125; 74 126])

Plot the solution from the direct method

fig, ax, sp = series(soldirect.t, soldirect.u', labels=["A", "B"]; axis=(;  xlabel="time", ylabel="# of molecules", title="SSA (direct method)"))
axislegend(ax)
fig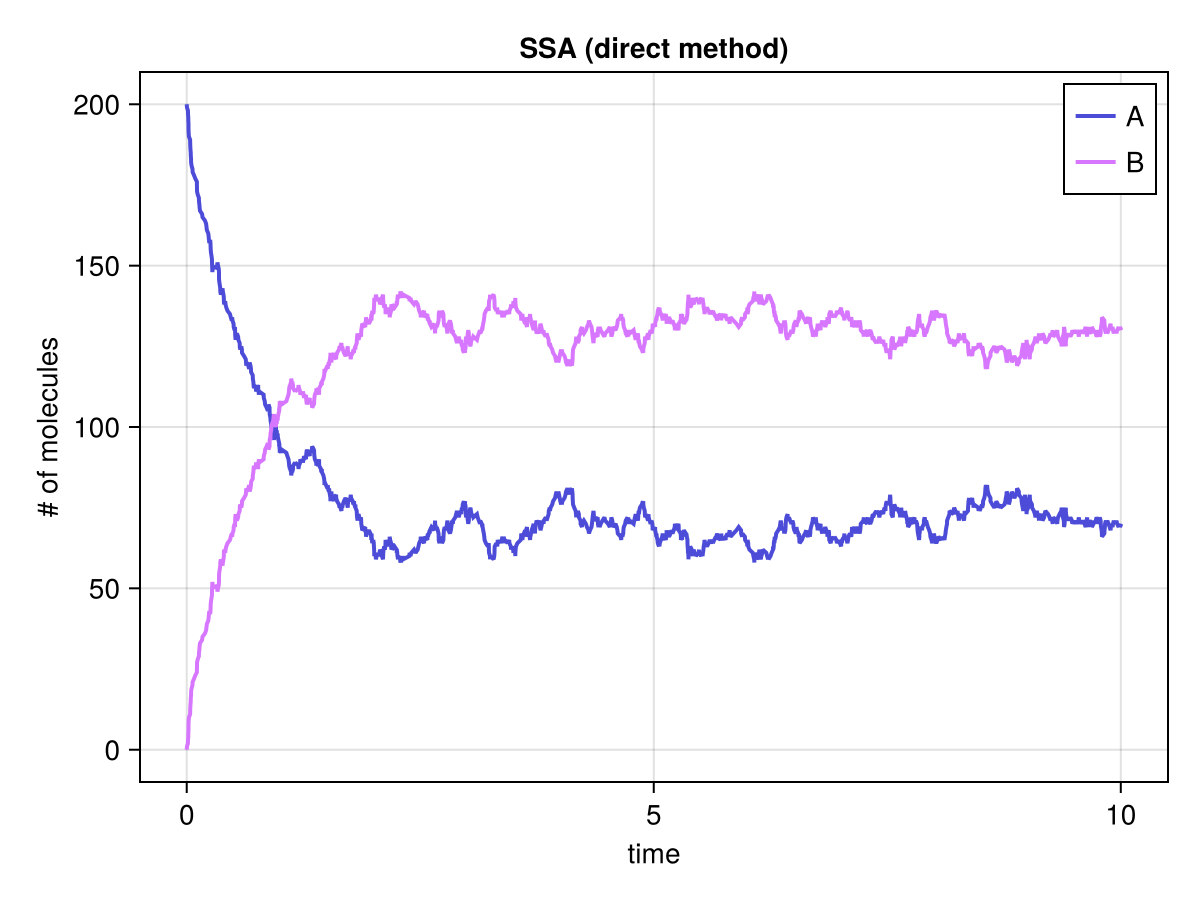

Plot the solution by the first reaction method

fig, ax, sp = series(solfirst.t, solfirst.u', labels=["A", "B"]; axis=(;  xlabel="time", ylabel="# of molecules", title="SSA (first reaction method)"))
axislegend(ax)
fig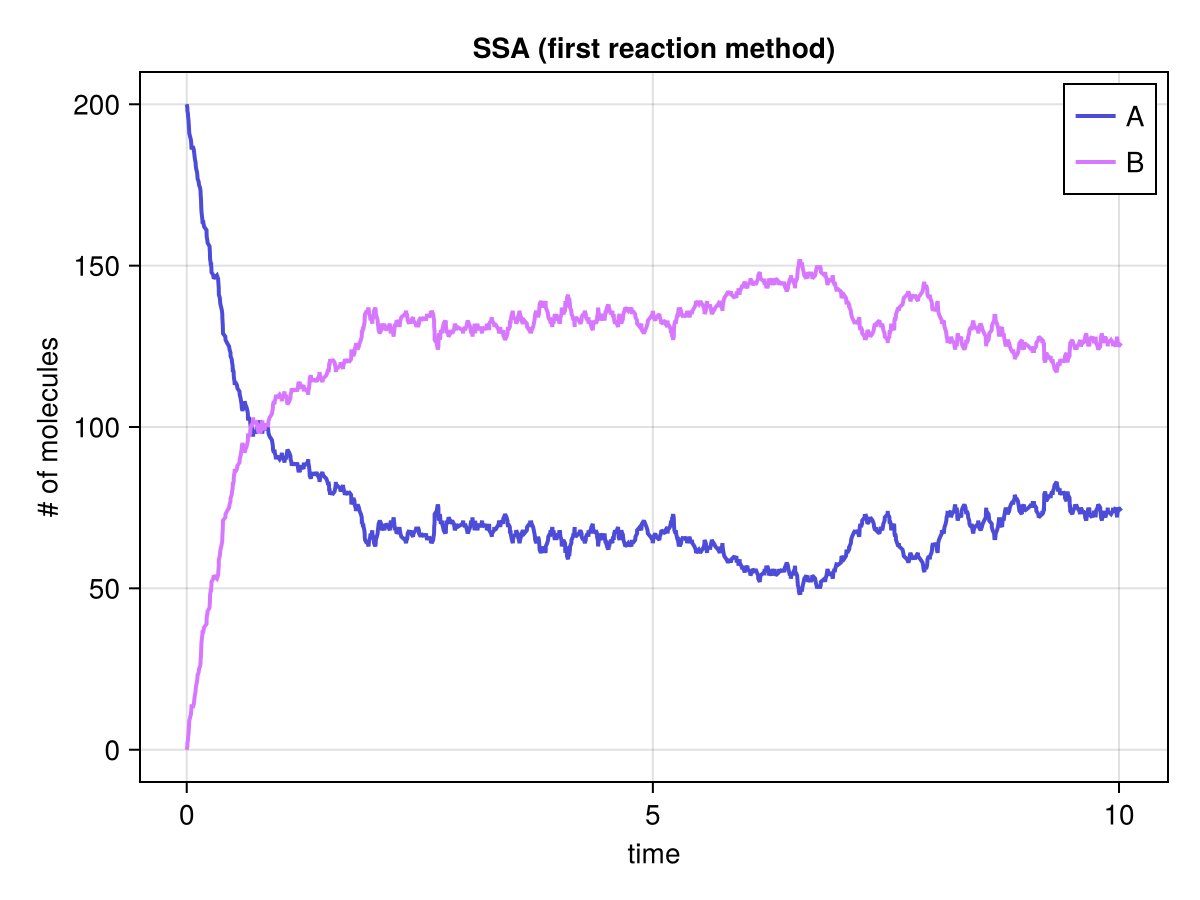

Running 50 simulations

@time sols = map(1:50) do _
    ssa_alg(model, u0, tend, parameters, stoich; method=:direct)
end;

  0.133689 seconds (635.51 k allocations: 760.284 MiB, 24.36% gc time, 39.54% compilation time)

Average values and interpolation

ts = range(0, tend, 101)
a_interp = [LinearInterpolation(sol.u[:, 1], sol.t; cache_parameters=true) for sol in sols]
b_interp = [LinearInterpolation(sol.u[:, 2], sol.t; cache_parameters=true) for sol in sols]
a_avg(t) = mean(i-> i(t), a_interp)
b_avg(t) = mean(i-> i(t), b_interp)

b_avg (generic function with 1 method)

Plot the solution

fig = Figure()
ax = Axis(fig[1, 1],
    xlabel = "Time",
    ylabel = "# of molecules",
    title = "SSA (first method) ensemble"
)
for sol in sols
    lines!(ax, sol.t, sol.u[:, 1], color = (:blue, 0.05))
    lines!(ax, sol.t, sol.u[:, 2], color = (:red, 0.05))
end
lines!(ax, ts, a_avg.(ts), color = :black, linewidth = 3, linestyle = :solid, label = "Average [A]")
lines!(ax, ts, b_avg.(ts), color = :black, linewidth = 3, linestyle = :dash, label = "Average [B]")
axislegend(ax, position = :rt)
fig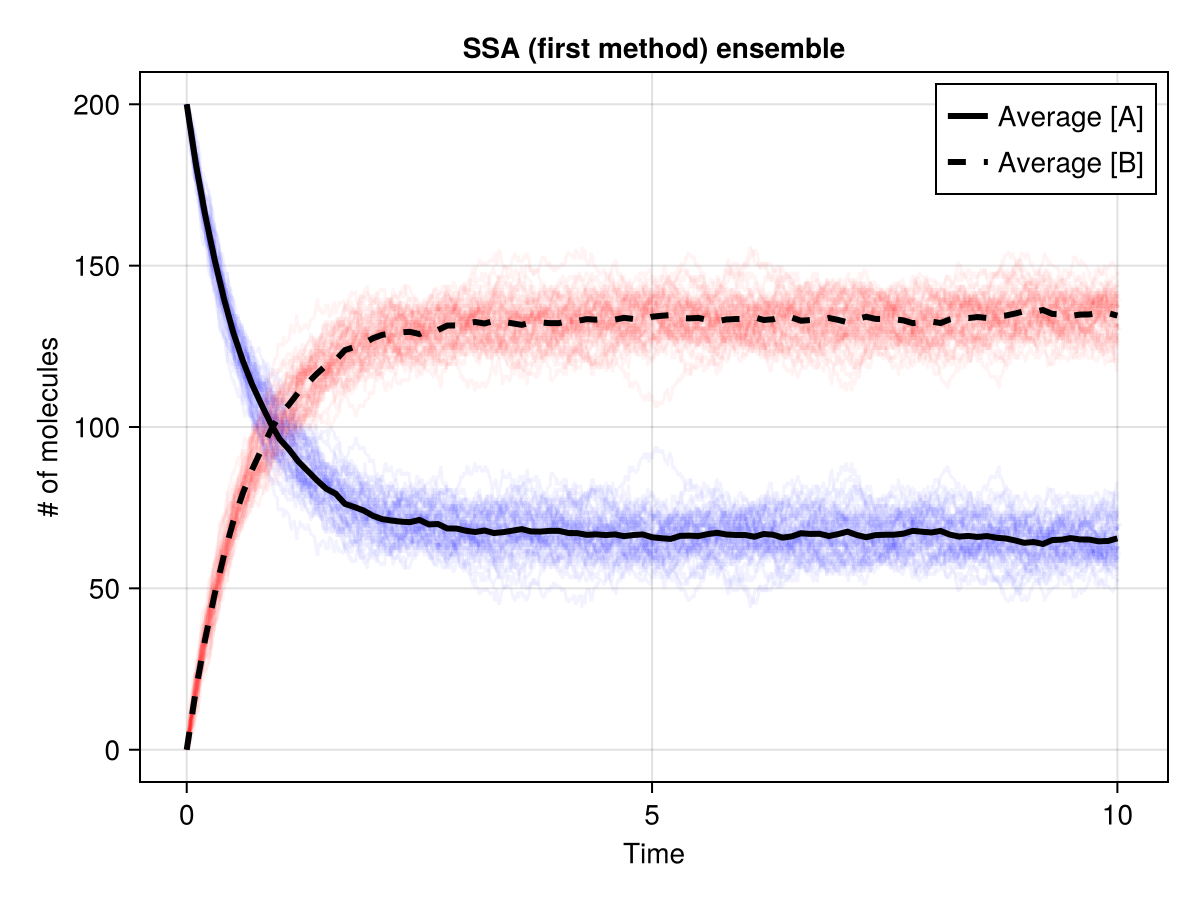

This notebook was generated using Literate.jl.