Fig 7.28 - MMSB

model of synthetic pulse generating system

using OrdinaryDiffEq
using ComponentArrays: ComponentArray
using SimpleUnPack
using CairoMakie

function model728!(D, u, p, t)
    @unpack aG, bG, KC, aC, bC, k1, k2, KR, RT, A = p
    @unpack G, C, R = u
    fR = R / KR
    fC = C / KC
    Gddt = -bG * G + aG * (fR / (1 + fR + fC^2 + fR * fC^2))
    Cddt = -bC * C + aC * R / (KR + R)
    Rddt = -k2 * R + k1 * (RT - 2 * R)^2 * A^2
    D.G = Gddt
    D.C = Cddt
    D.R = Rddt
    nothing
end

model728! (generic function with 1 method)

ps728 = ComponentArray(
    aG = 80, # muM/min
    bG = 0.07, # /min
    KC= 0.008, # muM
    aC= 0.5, # muM/min
    bC = 0.3, # /min
    k1 = 0.5, # /muM^3 /min
    k2 = 0.02, # /min
    KR= 0.02, # muM
    RT = 0.5, # muM
    A = 10.0, # muM
)

u0728 = ComponentArray(
    G = 0.0,
    C = 0.0,
    R = 0.0,
)

tend = 50.0
prob728 = ODEProblem(model728!, u0728, (0.0, tend), ps728)

ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(G = 1, C = 2, R = 3)}}} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 50.0)
u0: ComponentVector{Float64}(G = 0.0, C = 0.0, R = 0.0)

@time sol728 = solve(prob728, Tsit5())

  0.836419 seconds (4.76 M allocations: 317.220 MiB, 8.57% gc time, 99.99% compilation time)

retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 58-element Vector{Float64}:
  0.0
  9.999999999999999e-5
  0.0002808712273886078
  0.0005385770380686724
  0.0009134176741307914
  0.0014497117592804643
  0.002220241608899128
  0.003327456521230799
  0.00493088307190323
  0.0072784713692916995
  ⋮
 38.85909781274149
 40.56660938057199
 42.29446095428485
 43.93521921766175
 45.418101342448054
 46.747660381640486
 48.01058339261659
 49.30597743685047
 50.0
u: 58-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(G = 1, C = 2, R = 3)}}}}:
 ComponentVector{Float64}(G = 0.0, C = 0.0, R = 0.0)
 ComponentVector{Float64}(G = 0.00023928969093921896, C = 1.4955489953242168e-6, R = 0.001243779852809739)
 ComponentVector{Float64}(G = 0.001753727239505, C = 1.0960559299560879e-5, R = 0.0034622580928137456)
 ComponentVector{Float64}(G = 0.005866049357478844, C = 3.666147408118327e-5, R = 0.006555641145226796)
 ComponentVector{Float64}(G = 0.014951823136417011, C = 9.344608787095643e-5, R = 0.010918940492649123)
 ComponentVector{Float64}(G = 0.03249514346959783, C = 0.00020311322260303043, R = 0.016896395072320568)
 ComponentVector{Float64}(G = 0.06391046303714978, C = 0.00039969465252449665, R = 0.024979408364971294)
 ComponentVector{Float64}(G = 0.11692939783268566, C = 0.0007326265006532332, R = 0.0356591712345212)
 ComponentVector{Float64}(G = 0.2027201099542955, C = 0.0012771049211146106, R = 0.04944325418747299)
 ComponentVector{Float64}(G = 0.3361082146457654, C = 0.0021487700682468916, R = 0.06670084724114986)
 ⋮
 ComponentVector{Float64}(G = 0.1618686927818645, C = 1.540896555522915, R = 0.24509326625515915)
 ComponentVector{Float64}(G = 0.14684124743838672, C = 1.5408974093230676, R = 0.24511543421192836)
 ComponentVector{Float64}(G = 0.13335732756919702, C = 1.5408951709898615, R = 0.24518656060251717)
 ComponentVector{Float64}(G = 0.12197777443922539, C = 1.5408897297317679, R = 0.24535684146860398)
 ComponentVector{Float64}(G = 0.11275921374415801, C = 1.5408875188910272, R = 0.24557025743710703)
 ComponentVector{Float64}(G = 0.10526936958726163, C = 1.5409010351887436, R = 0.2455034853003446)
 ComponentVector{Float64}(G = 0.09877225763189024, C = 1.5409153479173887, R = 0.24528505208826476)
 ComponentVector{Float64}(G = 0.09267872739629743, C = 1.5409186638911982, R = 0.2451538818127746)
 ComponentVector{Float64}(G = 0.0896343815165816, C = 1.5409208331796385, R = 0.24507614538602768)

fig = Figure()
ax = Axis(fig[1, 1],
    xlabel = "Time (min)",
    ylabel = "Concentration (μM)",
    title = "Fig 7.28"
)
lines!(ax, 0..tend, t-> sol728(t).G, label = "GFP")
lines!(ax, 0..tend, t-> sol728(t).C, label = "cI")
lines!(ax, 0..tend, t-> sol728(t).R, label = "LuxR:AHL complex")
axislegend(ax, position = :rc)
fig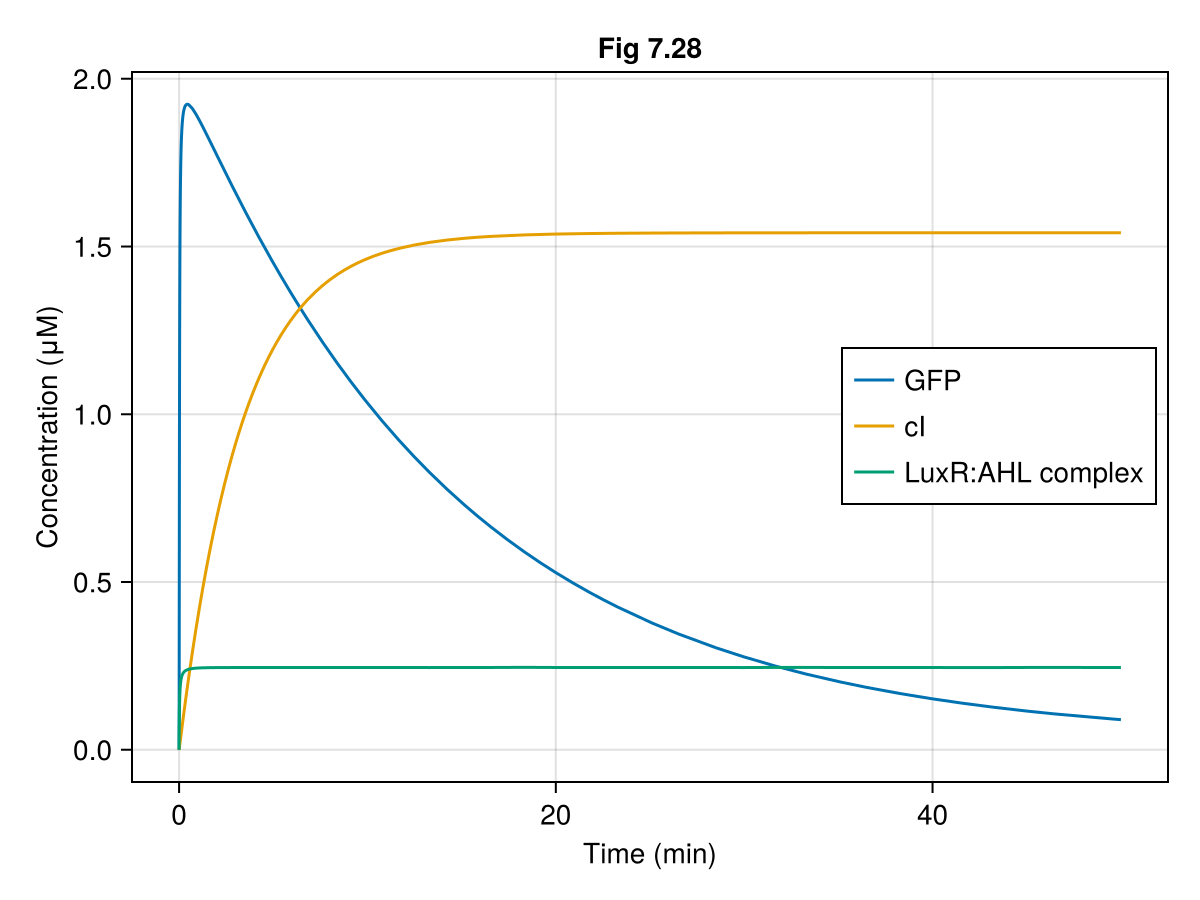

This notebook was generated using Literate.jl.