Fig 2.09 - MMSB

Metabolic network simulation

using OrdinaryDiffEq
using ComponentArrays: ComponentArray
using SimpleUnPack
using CairoMakie

function model209!(du, u, p, t)
    @unpack k1, k2, k3, k4, k5 = p
    @unpack A, B, C, D = u
    v1 = k1
    v2 = k2 * A
    v3 = k3 * A * B
    v4 = k4 * C
    v5 = k5 * D
    du.A = v1 - v2 - v3
    du.B = v2 - v3
    du.C = v3 - v4
    du.D = v3 - v5
    nothing
end

model209! (generic function with 1 method)

Setup problem

ps = ComponentArray(k1=3.0, k2=2.0, k3=2.5, k4=3.0, k5=4.0)
u0 = ComponentArray(A=0.0, B=0.0, C=0.0, D=0.0)
tend = 10.0
prob = ODEProblem(model209!, u0, tend, ps)

ODEProblem with uType ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(A = 1, B = 2, C = 3, D = 4)}}} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 10.0)
u0: ComponentVector{Float64}(A = 0.0, B = 0.0, C = 0.0, D = 0.0)

Solve the problem

@time sol = solve(prob, Tsit5())

  1.005278 seconds (4.86 M allocations: 324.143 MiB, 7.61% gc time, 100.00% compilation time)

retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 31-element Vector{Float64}:
  0.0
  9.999999999999999e-5
  0.0010999999999999998
  0.011099999999999997
  0.03427453254462915
  0.06522753353833287
  0.10153577459409753
  0.14533869701822555
  0.19788890020410435
  0.2619461233746949
  ⋮
  3.481141518838101
  4.1462374627542244
  4.984641398737613
  5.978883857784344
  6.9999177726334345
  7.954887766924096
  8.836082624890851
  9.672663483036162
 10.0
u: 31-element Vector{ComponentArrays.ComponentVector{Float64, Vector{Float64}, Tuple{ComponentArrays.Axis{(A = 1, B = 2, C = 3, D = 4)}}}}:
 ComponentVector{Float64}(A = 0.0, B = 0.0, C = 0.0, D = 0.0)
 ComponentVector{Float64}(A = 0.00029997000199933764, B = 2.999799953754866e-8, C = 5.623912546644786e-16, D = 5.623800072204464e-16)
 ComponentVector{Float64}(A = 0.003296372652316679, B = 3.627331236355826e-6, C = 8.218056460901692e-12, D = 8.216249166279005e-12)
 ComponentVector{Float64}(A = 0.0329330063952576, B = 0.00036682535223159696, C = 8.356768013816546e-8, D = 8.338285321893453e-8)
 ComponentVector{Float64}(A = 0.09937122761544223, B = 0.0034375565665459152, C = 7.255794159499436e-6, D = 7.206618524863435e-6)
 ComponentVector{Float64}(A = 0.1833655969433656, B = 0.01213116604059312, C = 8.93425388002502e-5, D = 8.820117939513295e-5)
 ComponentVector{Float64}(A = 0.2751746900149442, B = 0.02839992448709784, C = 0.0004856662162730563, D = 0.00047610712983925765)
 ComponentVector{Float64}(A = 0.37646083724449214, B = 0.055514839373642884, C = 0.0018497945329364433, D = 0.0017982532908780542)
 ComponentVector{Float64}(A = 0.48441969055278616, B = 0.0965602973248322, C = 0.005620960526037499, D = 0.0054101243611240964)
 ComponentVector{Float64}(A = 0.5961814643349724, B = 0.15505310630069288, C = 0.014714875647080206, D = 0.01399242839716861)
 ⋮
 ComponentVector{Float64}(A = 0.7510154814517538, B = 0.7988628794584909, C = 0.49983459077320186, D = 0.37494915708414317)
 ComponentVector{Float64}(A = 0.7502915599254341, B = 0.7996724577481669, C = 0.4999584903912881, D = 0.37498115400855303)
 ComponentVector{Float64}(A = 0.7500631110964758, B = 0.799930520868622, C = 0.4999887838283953, D = 0.3749895487365714)
 ComponentVector{Float64}(A = 0.7500144275982006, B = 0.799988235984439, C = 0.4999904564213279, D = 0.3749708607822979)
 ComponentVector{Float64}(A = 0.7500125250580956, B = 0.7999980647430993, C = 0.49997804770112764, D = 0.3748883744178732)
 ComponentVector{Float64}(A = 0.7500190130496599, B = 0.7999996560465512, C = 0.4999625081714845, D = 0.3747465332743288)
 ComponentVector{Float64}(A = 0.7500193831308758, B = 0.7999999319182717, C = 0.4999613387386591, D = 0.37467706324895206)
 ComponentVector{Float64}(A = 0.7500144341539193, B = 0.7999999855119416, C = 0.4999711542724638, D = 0.37471457052262475)
 ComponentVector{Float64}(A = 0.7500039199737641, B = 0.7999999921573434, C = 0.499992172536642, D = 0.37492503636480035)

Visualize the results

ts = range(0, tend, length=100)
us = Array(sol(ts))
fig, ax, sp = series(ts, us, labels=["A", "B", "C", "D"], axis=(title="Fig 2.9\nMetabolic Network Simulation", xlabel="Time", ylabel="Concentration"))
axislegend(ax, position=:rb)
fig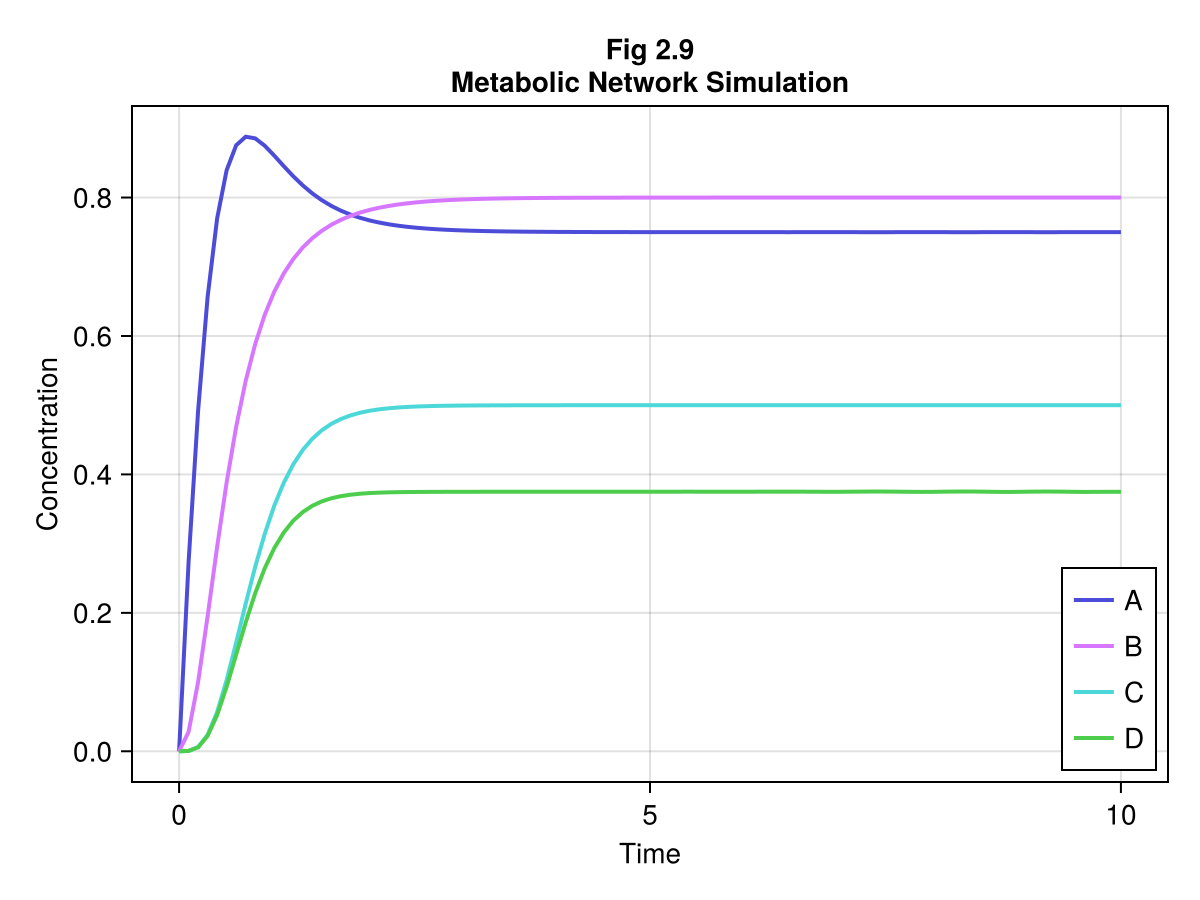

This notebook was generated using Literate.jl.